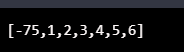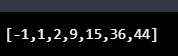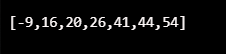Updated March 17, 2023
Introduction to Sorting Algorithms in JavaScript
Similar to most other programming languages, you can run into scenarios where you have to sort some numbers in JavaScript into ascending or descending order. To get it done, we can use many algorithms such as Bubble sort, Selection Sort, Merge sort, Quicksort, etc. These algorithms not only differ in how they work but also each has its different demands in terms of memory and time took, let’s dig deeper into some of the important sorting algorithms and see how you can use them in your JavaScript code.
Top 6 Sorting Algorithms in JavaScript
Here are some sorting algorithms in javascript explained below with examples:
1. Bubble Sort Algorithm
Considered to be one of the most common tools of this trade, Bubble sort works by creating a loop that compares each item in the array with another item. If the compared item is smaller than the one on hand, we swap their places. This keeps on going until we have a pass where no item in the array is bigger than the item that is next to it.
Bubble Sort has O(n2) time complexity and O(n) space complexity.
Code:
function swap(arr, firstIndex, secondIndex){
var temp = arr[firstIndex];
arr[firstIndex] = arr[secondIndex];
arr[secondIndex] = temp;
}
function bubbleSortAlgo(arraaytest){
var len = arraaytest.length,
i, j, stop;
for (i=0; i < len; i++){
for (j=0, stop=len-i; j < stop; j++){
if (arraaytest[j] > arraaytest[j+1]){
swap(arraaytest, j, j+1);
}
}
}return arraaytest;
}
console.log(bubbleSortAlgo([3, 6, 2, 5, -75, 4, 1]));Output:
2. Selection Sort Algorithm
Now that we are done discussing the Bubble Sort Algorithm, let’s take a look at just as a popular algorithm for sorting called Selection Sort.
Unlike Bubble Sort, we focus on finding the smallest value in the array to get the sorting done. Here is a step by step breakdown of how Selection Sort works:
- We assume the first item in the array as the smallest one.
- We compare this item to the next item in the array.
- If the next item is smaller than the one at hand, we set the next item as the new smallest value.
- We keep repeating these steps until we reach the end of the array.
- When we find value in the array that is smaller than the one we started with, we swap their positions.
- We keep doing the comparisons and moving to the next item. Until the entire array is sorted.
Just like the Bubble Sort algorithm, the Selection sort has O(n2) time complexity and O(n) space complexity.
Code:
function SelectionSortAlgo(array, compare_Function) {
function comp(a, b) {
return a - b;
}
var min = 0;
var index = 0;
var temp = 0;
compare_Function = compare_Function || compare;
for (var i = 0; i < array.length; i += 1) {
index = i;
min = array[i];
for (var j = i + 1; j < array.length; j += 1) {
if (compare_Function(min, array[j]) > 0) {
min = array[j];
index = j;
}
}
temp = array[i];
array[i] = min;
array[index] = temp;
}
return array;
}
console.log(SelectionSortAlgo([9, 15, 2, 44, -1, 36, 1], function(a, b) { return a - b; }));Output:
3. Merge Sorting Algorithm
Similar to Bubble Sort and Selection Sort, Merge sort is one of the popular sorting algorithms in computer science, you can implement it in most programming languages, and it has good performance without it being too needy on resources.
Merge Sort uses Divide and conquer method to sort an array or any list of elements. The term divides and conquers means we divide one big problem into several smaller problems and then we solve these small problems. Once the smaller problems are solved, we combine the results which result in the solution to the big problem.
Understanding the algorithm is simple actually:
- We divide the given array into n arrays each of these arrays contains just 1 element.
- Merge the arrays to produce a new array.
- Repeat step 2 until there is only 1 array remaining, which will be the sorted array.
Code:
function merge_sort_algo(left,right)
{
var i = 0;
var j = 0;
var result = [];
while (i < left.length || j < right.length) {
if (i === left.length) {
// j is the only index left_part
result.push(right[j]);
j++;
}
else if (j === right.length || left[i] <= right[j]) {
result.push(left[i]);
i++;
} else {
result.push(right[j]);
j++;
}
}
return result;
}
console.log(merge_sort_algo([1,44,6], [84,7,5]));Output:
4. Quick Sort Algorithm
Quicksort is one of the most efficient ways of sorting elements in computer systems. Similor to merge sort, Quicksort works on the divide and conquer algorithm. In this, we find a pivot item in the array to compare all other elements arrays against and then we move the items in a way where all items before our selected pivot items are smaller and all items after the pivot item are larger in size. Once we have done that, the key is to keep doing it repeatedly and we will have our sorted array.
Following are the steps that can be followed to implement quicksort algorithm:
- We select an element of the array and call it “Pivot Point”
- We start a pointer called the left pointer from which is at the first element in the array.
- Similarly, we start a pointer called the right pointer at the last item in the array.
- If the value of the element at the left pointer is less compared to the selected pivot point, we move the left pointer leftwards (add +1 to it) and keep repeating it until the value at the left pointer is found to be bigger than the value of pivot point or equal to it.
- If the value of the element at the right pointer in the list is higher than the value of the pivot element, we mode the right pointer to left. Repeat this until the value at the right side pointer is lower than (or equal to) the value of pivot.
- When the value of the left pointer is less than or equal to the value of the right pointer, swap the values.
- Move the right pointer to left by one, left pointer to right by one.
- Repeat until left and right pointers meet.
Code:
function quickSortAlgo(origArray) {
if (origArray.length <= 1) {
return origArray;
} else {
var left = [];
var right = [];
var newArray = [];
var pivot = origArray.pop();
var length = origArray.length;
for (var i = 0; i < length; i++) {
if (origArray[i] <= pivot) {
left.push(origArray[i]);
} else {
right.push(origArray[i]);
}
}
return newArray.concat(quickSortAlgo(left), pivot, quickSortAlgo(right));
}
}
var myArray = [13, 50, 2, 45, -1, 74, 11 ];
var arreySorted = quickSortAlgo(myArray);
console.log(arreySorted);Output:
5. Insertion Sort Algorithm
When it comes to ease of implementation, insertion sort is widely known as one of the simpler algorithms. In Insertion Sort, elements of the array are compared to each other and then arranged in a particular order. This is very similar to arranging cards in a deck. The name insertion sort comes from the process of picking an element and inserting it in its correct place and then repeating it for all elements.
Here is how the algorithm works:
- The first element of the array is considered already sorted.
- Pick the next element of the array.
- Compare the selected element with all elements in the array.
- Shift every element in the array which is greater than the value of the selected element.
- Insert the element
- Repeat Step 2 to 5 until the array is sorted.
Code:
function insertion_Sort_algo(arr)
{
for (var i = 1; i < arr.length; i++)
{
if (arr[i] < arr[0])
{
arr.unshift(arr.splice(i,1)[0]);
}
else if (arr[i] > arr[i-1])
{
continue;
}
else {
for (var j = 1; j < i; j++) {
if (arr[i] > arr[j-1] && arr[i] < arr[j])
{
arr.splice(j,0,arr.splice(i,1)[0]);
}
}
}
}
return arr;
}
console.log(insertion_Sort_algo([44, 20, 26, 54, -9, 41, 16]));Output:
6. Heap Sort Algorithm
Heap sorting is a way of sorting elements by using the “Heap” data structure. The method is quite similar to the selection sort technique we discussed earlier. Now you may be wondering about Heaps and how are they defined, before getting to the algorithm, let’s understand heaps first.
In a nutshell, a heap is a binary tree with some added rules. One rule states that in heap, the tree must be a complete binary tree which simply means that it is necessary to fill all nodes on the current level before adding another one. The next rule for the heap is that there must be a defined child and parent relationship with the element values of the heap.
In a min-heap, the value of a parent must be smaller than its children. In a max heap, as you can guess, the value of a parent must be greater than its child.
Now that definitions are out of the way, let’s take a look at how heapsort works:
- We first build a max heap which makes sure that the highest value element is at the top.
- We switch the top element with the last element of the heap and remove the top element from the heap and store it on a sorted array.
- We keep repeating the step one and two until there is only one element remains in the heap.
One thing to keep in mind is that Heaps are not natively supported in JavaScript, therefore we have to resort at implementing Heaps using arrays. The space complexity of heap sort is O(1) which is excellent and while it is a bit more complicated compared to merge sort or insertion sort when it comes to understanding and implementation, I think for performance benefits, it is ultimately better to use in large projects.
Code:
var arrLength;
function heapRoot(input, i) {
var left = 2 * i + 1;
var right = 2 * i + 2;
var max = i;
if (left < arrLength && input[left] > input[max]) {
max = left;
}
if (right < arrLength && input[right] > input[max]) {
max = right;
}
if (max != i) {
swap(input, i, max);
heapRoot(input, max);
}
}
function swap(input, index_A, index_B) {
var temp = input[index_A];
input[index_A] = input[index_B];
input[index_B] = temp;
}
function heapSortAlgo(input) {
arrLength = input.length;
for (var i = Math.floor(arrLength / 2); i >= 0; i -= 1) {
heapRoot(input, i);
}
for (i = input.length - 1; i > 0; i--) {
swap(input, 0, i);
arrLength--;
heapRoot(input, 0);
}
}
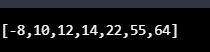
var arr = [12, 10, 22, 55, -8, 64, 14];
heapSortAlgo(arr);
console.log(arr);Output:
Conclusion
Sorting is an important part of creating applications and websites with JavaScript. Now that you are familiar with some of the most important algorithms to get the job done, you should feel more confident in JS Development.
One important fact to keep in mind about various sorting is that you don’t really have to stress yourself too much regarding what algorithm to use in most of the cases. Now that the computer hardware is so powerful, modern phone and Desktop processors won’t break any sweat in sorting even hundreds of elements in a few milliseconds. It is only cases where you are stuck with slow hardware or situations where you mush optimize every single section of code where changing sorting algorithms can be beneficial.
Recommended Articles
This is a guide to Sorting Algorithms in JavaScript. Here we discuss the top 6 sorting algorithms in javascript along with examples & code implementation. You may also look at the following articles to learn more –