Updated April 11, 2023
Introduction to Sorting in JavaScript
Sorting is the most common technique used in programming. Sorting is nothing but arranging elements in sequential order. For instance, if we want to sort the name of a state or country in ascending or descending order then, we need to use a sorting algorithm. There are many types of sorting algorithms available in Jscript that sort the array or elements effectively. The most important need for sorting is that data searching in a large database can be optimized to a very larger level. If the data stored in sorted order. For example, let take the Telephone Directory where it has telephone numbers are sorted according to the names of the person so that the search can be easily done.
How sorting is performed in JavaScript?
Let’s take some random array of elements with everything jumbled. For example, take [ 8,5,3,6,2 ] and you want that to be sorted as [ 2,3,5,6,8 ] using a sorting algorithm. For example, the element will be taken from the left of the array for sorting and compare it with an adjacent element in the array. If the first element is greater than the adjacent element then, we switch the element. Then, we compare the second element in the array to the next element. The element will be switched if it is out of order. This process keeps repeating until we reach the end of the array.
Example for sorting:
| // Start with an unsorted array | |
| [ 9, 8, 3, 7, 2 ] | |
| // Check the elements in pairs and flip them as needed: | |
| // 9 > 8 9 > 3 9 > 7 9 > 2 | |
| [ 8, 9, 3, 7,2 ], [ 8, 3, 9, 7, 2 ], [ 8, 3, 7, 9, 2 ], [ 8, 3, 7, 2, 9 ] | |
| // Repeat: | |
| [ 3, 8, 7, 2, 9 ], [ 3, 7, 8, 2, 9 ], [ 3, 7, 2, 8, 9 ], [ 3, 7, 2, 8, 9 ] | |
| [ 3, 7, 2, 8, 9 ], [ 3, 2, 7, 8, 9 ], [ 3, 2, 7, 8, 9 ], [ 3, 2, 7, 8, 9 ] | |
| [ 2, 3, 7, 8, 9 ], … |
Types of Sorting algorithm in JavaScript
Below are the different types of Sorting algorithm in JavaScript
- Bubble Sort
- Insertion Sort
- Merge Sort
- Quick Sort
- Selection Sort
1. Bubble Sort
Bubble sort is performed by repeatedly sorting the array element by comparing the adjacent elements. It compares the adjacent element and it swaps the element if they are in the wrong order. This algorithm runs repeatedly until all the elements in the lists are sorted. If all the elements sorted in the list, then the algorithms end automatically. Although the bubble sort algorithm is simple, it consumes more time comparing other sorting techniques.
How bubble sort works in JavaScript?
- In Bubble Sort, the algorithm will take 1st element of the array and compare the value with the element next to it in the array.
- If the 1st element is larger than the 2nd, then the element will swap the positions.
- If it doesn’t satisfy the condition, then the algorithm will compare 2nd element with 3rd
- This process continues until all the elements in the array is bubble sorted in the respective order.
Example #1
Code:
<html>
<head>
<title> Bubble Sort </title>
</head>
<body>
<script>
function bubblesort (a,N)
{
var i=j=v=0;
for (i=1; i<N; i++)
{
v = a[i];
j = i;
while (j>0 && a[j-1]>v)
{
a[j] = a[j-1];
j--;
};
a[j] = v;
}
for (i=0; i<a.length; i++)
{
};
};
var x = [9,4,5,2,1,6,7,0,3];
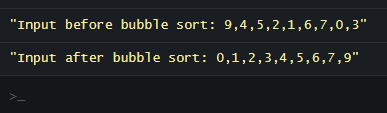
console.log("Input before bubble sort: " +x);
bubblesort(x,9);
console.log("Input after bubble sort: " +x);
</script>
</body>
</html>Output:
Example #2
Code:
<html>
<head>
<title> Bubble Sort </title>
</head>
<body>
<script>
function bubbleSort(array)
{
var flag = true; //checks to see if any swaps are made
while (flag)
{
flag = false; //if flag remains false, then the list is already sorted as no swaps are necessary
for (var i = 0; i < array.length - 1; i++) { //program terminates when this "if" is not accessed
if (array[i] > array[i + 1])
{
var temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
flag = true; //if swap occurs, flag is changed to true and process repeats
}
}
}
}
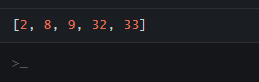
var myArray = [32, 33, 8, 2, 9];
bubbleSort(myArray);
console.log(myArray);
</script>
</body>
</html>Output:
2. Insertion Sort
Insertion sorting algorithm works by dividing the unsorted array into 2 categories, sorted category, and unsorted category. First, the sorted category will have one element which is sorted element. Then, we select the unsorted category element one by one. Insert the elements in the sorted category at the correct position.
Example #1
Code:
<html>
<body>
<script>
function InsertionSort(arr)
{
let len = arr.length, value, i, j;
for(i = 1; i < len; i++)
{
value = arr[i];
j = i - 1;
while (j >= 0 && arr[j] > value)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = value;
}
return arr;
}
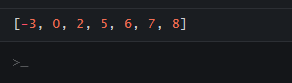
var myArray = [5,8,-3,2,7,0,6];
InsertionSort(myArray);
console.log(myArray);
</script>
</body>
</html>Output:
Example #2
Code:
<html>
<body>
<script>
function insertionSort(inputArray)
{
var totalElements = inputArray.length - 1;
var temp = 0;
var lastIndex = 0;
var prevIndex = 0;
for(var i = 0;i <= totalElements;i++)
{
for(var currentIndex = i; currentIndex > lastIndex; currentIndex--)
{
prevIndex = currentIndex - 1;
if(inputArray[currentIndex] < inputArray[prevIndex]){
temp = inputArray[currentIndex];
inputArray[currentIndex] = inputArray[prevIndex];
inputArray[prevIndex] = temp;
}
else
break;
}
}
return inputArray;
}
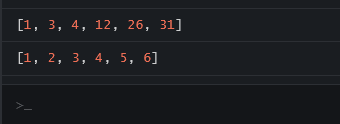
console.log(insertionSort([1,31,26,4,3,12]));
console.log(insertionSort([5,6,1,2,3,4]));
</script>
</body>
</html>Output:
3. Merge Sort
The merge sort algorithm is the most used sorting algorithm by programmers. The concept used in this algorithm is divide and conquer for sorting an array of elements. It will divide the larger group of elements into a smaller groups. Then, it sorts that smaller group of elements to sort the larger group. The merger sort is easy to understand and implement comparing another sorting algorithm.
Example #1
Code:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>JavaScript program of Merge sort</title>
</head>
<body>
<script>
function merge_sort(left_part,right_part)
{
var i = 0;
var j = 0;
var results = [];
while (i < left_part.length || j < right_part.length) {
if (i === left_part.length) {
// j is the only index left_part
results.push(right_part[j]);
j++;
}
else if (j === right_part.length || left_part[i] <= right_part[j]) {
results.push(left_part[i]);
i++;
} else {
results.push(right_part[j]);
j++;
}
}
return results;
}
console.log(merge_sort([1,3,4], [3,7,9]));
</script>
</body>
</html>Output:
Example #2
Code:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title> JavaScript program of Merge sort </title>
</head>
<body>
<script>
function mergeSort(data)
{
if(data.length == 1 ) return data;
var mid = data.length / 2;
var left = data.slice(0, mid);
var right = data.slice(mid);
left = mergeSort(left);
right = mergeSort(right);
return merge(left, right);
}
function merge(left, right)
{
var result=[];
var leftIndex=0;
var rightIndex=0;
while(leftIndex<left.length && rightIndex<right.length)
{
if(left[leftIndex]>right[rightIndex])
{
result.push(right[rightIndex]);
rightIndex++;
}
else
{
result.push(left[leftIndex]);
leftIndex++;
}
}
while(leftIndex<left.length)
{
result.push(left[leftIndex]);
leftIndex++;
}
while(rightIndex<right.length)
{
result.push(right[rightIndex]);
rightIndex++;
}
return result;
}
console.log(insertionSort([1,31,26,4,3,12]));
console.log(insertionSort([5,6,1,2,3,4]));
</body>
</script>
</html>Output:
4. Quick Sort
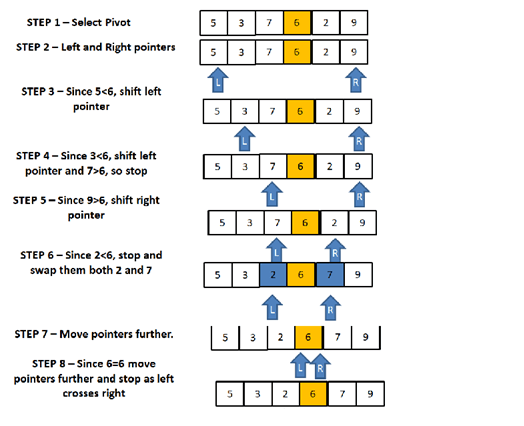
The quicksort also follows the same technique as merge sort which is divide and conquer. It performs by dividing larger elements into smaller groups and based on the condition it performs sorting of elements on the smaller group. In quick sort, we take one element as a Pivot element. The pivot element is the element that is in the middle of the array. From the pivot element we do the other element which is in right and left of the array.
Example #1
Code:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title> JavaScript program of Merge sort </title>
</head>
<body>
<script>
function QuickSort(arr, left = 0, right = arr.length - 1) {
let len = arr.length,
index
if(len > 1) {
index = partition(arr, left, right)
if(left < index - 1) {
QuickSort(arr, left, index - 1)
}
if(index < right) {
QuickSort(arr, index, right)
}
}
return arr
}
function partition(arr, left, right) {
let middle = Math.floor((right + left) / 2),
pivot = arr[middle],
i = left, // Start pointer at the first item in the array
j = right // Start pointer at the last item in the array
while(i <= j) {
// Move left pointer to the right until the value at the
// left is greater than the pivot value
while(arr[i] < pivot) {
i++
}
// Move right pointer to the left until the value at the
// right is less than the pivot value
while(arr[j] > pivot) {
j--
}
// If the left pointer is less than or equal to the
// right pointer, then swap values
if(i <= j) {
[arr[i], arr[j]] = [arr[j], arr[i]] // ES6 destructuring swap
i++
j--
}
}
return i
}
console.log(QuickSort([24,2,45,20,56,75,2,56,99,53,12]));
</script>
</body>
</html>Output:
Example #2
Code:
<html>
<head>
<meta charset="utf-8">
<title>JavaScript program of Quick sort</title>
</head>
<body>
<script>
function quick_Sort(origArray)
{
if (origArray.length <= 1)
{
return origArray;
}
else
{
var left = [];
var right = [];
var newArray = [];
var pivot = origArray.pop();
var length = origArray.length;
for (var i = 0; i < length; i++)
{
if (origArray[i] <= pivot)
{
left.push(origArray[i]);
} else {
right.push(origArray[i]);
}
}
return newArray.concat(quick_Sort(left), pivot, quick_Sort(right));
}
}
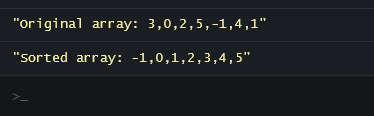
var myArray = [3, 0, 2, 5, -1, 4, 1 ];
console.log("Original array: " + myArray);
var sortedArray = quick_Sort(myArray);
console.log("Sorted array: " + sortedArray);
</script>
</body>
</html>Output:
5. Selection Sort
It is the simplest sorting technique. In this algorithm, you need to loop through the array in a linear method by selecting 1st smallest element, then swapping the smallest element to the 1st position. Then again, we must check the array linearly and select the 2nd smallest element. Then, move the 2nd smallest element in the 2nd position and continue the sorting process until the array is sorted completely. Example:
- [ 5, 4, 2, 1]
- The selection sort will consider 5 as the min element and will compare it with the remaining elements of the array. If any element in the array is smaller than 5 then it will be swapped.
- [1, 4, 2, 5]
- After the swapping is completed, now select 4 as a min element and compare with the rest of the array. 2 is smaller than 4. So, it will be swapped.
- This process is continued until the array is sorted completely.
The sorted output will be [ 1, 2, 4, 5 ].
Example #1
Code:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>JavaScript program of Selection sort</title>
</head>
<body>
<script>
function Selection_Sort(arr, compare_Function)
{
function compare(a, b)
{
return a - b;
}
var min = 0;
var index = 0;
var temp = 0;
//{Function} compare_Function Compare function
compare_Function = compare_Function || compare;
for (var i = 0; i < arr.length; i += 1) {
index = i;
min = arr[i];
for (var j = i + 1; j < arr.length; j += 1) {
if (compare_Function(min, arr[j]) > 0) {
min = arr[j];
index = j;
}
}
temp = arr[i];
arr[i] = min;
arr[index] = temp;
}
//return sorted arr
return arr;
}
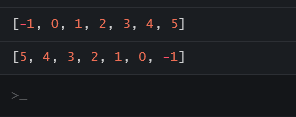
console.log(Selection_Sort([3, 0, 2, 5, -1, 4, 1], function(a, b) { return a - b; }));
console.log(Selection_Sort([3, 0, 2, 5, -1, 4, 1], function(a, b) { return b - a; }));
</script>
</body>
</html>Output:
Example #2
Code:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>JavaScript program of Selection sort</title>
</head>
<body>
<script>
function selection_sort(A) {
var len = array_length(A);
for (var i = 0; i < len - 1; i = i + 1) {
var j_min = i;
for (var j = i + 1; j < len; j = j + 1) {
if (A[j] < A[j_min]) {
j_min = j;
} else {}
}
if (j_min !== i) {
swap(A, i, j_min);
} else {}
}
}
function swap(A, x, y) {
var temp = A[x];
A[x] = A[y];
A[y] = temp;
}
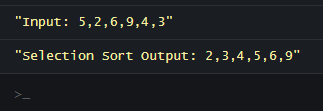
var myArray = [ 5, 2, 6, 9, 4, 3 ];
console.log("Input: " + myArray);
var sortedArray = selection_sort(myArray);
console.log("Selection Sort Output: " + sortedArray);
</script>
</body>
</html>Output:
Conclusion
We must learn simple programming concepts first in order to write complex programming in the future. The sorting algorithm concept is used in many complex programs to reduce the difficulty in sorting a database or list of things. From the above article, you can learn many sorting algorithm techniques. If you want to increase the consistency and performance in your program, then using the sorting algorithm is not a bad idea.
Recommended Articles
This is a guide to Sorting in JavaScript. Here we discuss the Introduction, How sorting performed in JavaScript?, Types of Sorting algorithm in JavaScript with example. You may also have a look at the following articles to learn more –