Updated March 18, 2023
Introduction to Sorting Algorithms in Python
Sorting the data in any and all systems is an efficient feature that helps keep the table/ database in an organized and structured format. It is a process of arranging the retrieved data in a specific pattern or order according to the given requirement. In python, this is carried out using various sorting algorithms, like the bubble sort, selection sort, insertion sort, merge sort, heap sort, and the radix sort methods.
Top 6 Sorting Algorithms in Python
Below are the different sorting algorithms for python:
1. Bubble Sort
Bubble sort is among the most commonly used sorting techniques; starting from the first two pair of elements, it involves sorting a series of elements by comparing every adjacent pair of elements. so when a misaligned order is established, then swapping of elements takes place. Until the last element in the input set, the above process is continued perceptibly, to optimize the algorithm, we call for to stop it after it has completed sorting. How possibly will we make out that we’ve completed sorting? this could be determined when all the given items are in order. So, whenever variables are swapped, a flag could be maintained to determine the sorting process’s re-execution. The flag should be set to false when no other swaps are needed.
Code:
def bubble_Sort(array):
length = len(array)
# loop through each and every element which are keyed
# loop through each and every element which are keyed
for iterator_1 in range(length):
#loop through next element
for iterator_2 in range(0, length-iterator_1-1):
# From 0 to n-i-1 the array value needs to be looped upon
# when a element greater than the next element then the collected element needs to be swapped.
if array[iterator_2] > array[iterator_2 + 1] :
array[iterator_2], array[iterator_2 + 1] = array[iterator_2 + 1], array[iterator_2]
# Driver code to test above
array = [75,34,54,56,78,1]
bubble_Sort(array)
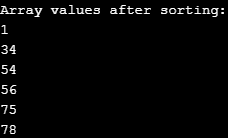
print ("Array values after sorting:")
for i in range(len(array)):
print ("%d" %array[i])
Output:
2. Selection Sort
Selection sorting is among the most basing sorting techniques. This technique involves finding the least or minimum element from the unsorted set and positioning that element at the beginning of the unsorted set. On looping these operations across all elements in the set, a completely sorted set can be achieved. The algorithm segregates the key list hooked on two different parts. The inner list or the subscription list tend to be already sorted, which involves generating from the leftmost element to the rightmost element, and the sub listing of items outstanding to be sorted that inhabit the respite of the list. At first, the sorted sublist is unfilled, and the unsorted sublist is the complete key list.
Code:
import sys
Array = [63, 75, 13, 2, 441]
# loop through each and every element in the array
for element1 in range(len(Array)):
# To determine the least element in the remaining list
minimum_idx = element1
for element2 in range(element1+1, len(Array)):
if Array[minimum_idx] > Array[element2]:
min_idx = element2
# swap the determined least element with the previous element in the list
Array[element1], Array[minimum_idx] = Array[minimum_idx], Array[element1]
# main code
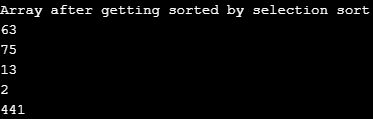
print ("Array after getting sorted by selection sort")
for i in range(len(Array)):
print("%d" %Array[i]),
Output:
3. Insertion Sort
In Insertion sorting, the sorting mechanism is carried out by building a sorted array with one item at a time. the elements of the array are compared in a sequential manner and then rearranged in one specific order. The components of the array are compared sequentially to each of the elements and then ordered simultaneously in a specific order. The analogy used here is very similar to arranging a set of cards.
Code:
def insertion_Sort(array):
# pass through through 1 to len(array)
for temp_element1 in range(1, len(array)):
key = array[temp_element1]
# Move elements of array[0..i-1], that are
# greater than key, to one position ahead
# of their current position
temp_element2 = temp_element1 -1
while temp_element2 >= 0 and key < array[temp_element2] :
array[temp_element2 + 1] = array[temp_element2]
temp_element2 -= 1
array[temp_element2 + 1] = key
# Driver code to test above
array = [75,34,54,56,78,1]
insertion_Sort(array)
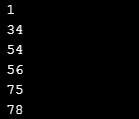
for i in range(len(array)):
print ("% d" % array[i])
Output:
4. Merge Sort
The Merge sort works on the principle of divide and conquers algorithm. Here the given input is spliced into two halves, and the spliced halves are sorted and then merged. In python perception, the merge() function is used for achieving the merge process. the algorithm for insertion sort is like below,
- The mentioned array needs to be split into two different parts, and the median of the array is determined for this.
- Merge sort is applied in the first half of the split.
- Then the second half is also exposed to the same.
- At last, after sorting, the segregated halves are merged.
Code:
def merge_Sort(array):
if len(array) >1:
mid = len(array)//2 #determining the mid of the array
divide = array[:mid] # Dividing the array elements
split = array[mid:] # splitting the array into 2 halves
merge_Sort(divide) # first half of the sorting
merge_Sort(split) # second half of the sorting
i = j = k = 0
# Copy data to temp arrayays divide[] and split[]
while i < len(divide) and j < len(split):
if divide[i] < split[j]:
array[k] = divide[i]
i+=1
else:
array[k] = split[j]
j+=1
k+=1
# Checking if any element was left
while i < len(divide):
array[k] = divide[i]
i+=1
k+=1
while j < len(split):
array[k] = split[j]
j+=1
k+=1
# Code to print the list
def printdivideist(array):
for i in range(len(array)):
print(array[i],end=" ")
print()
# driver code to test the above code
if __name__ == '__main__':
array = [12, 2, 93, 65, 76, 27]
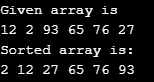
print ("Given arrayay is", end="\n")
printdivideist(array)
merge_Sort(array)
print("Sorted arrayay is: ", end="\n")
printdivideist(array)
Output:
5. Heap Sort
Heap sort is a form of selection sorting technique. It involves segregating the given input as sorted and non-sorted elements. Then the algorithm loops in such a manner on the non sorted region so that on each loop, the largest value will be pushed into the sorted region. This process will be continued across all the elements in the unsorted region.
A max heap is created from the given input list. The last value is then swapped with the first value repeatedly, and also, the value range is comparatively decreased by one. This process takes place until the range shrinks to 1.
Code:
def heap_sort(Ordering, number, i):
largest = i # Initialize largest as root
left= 2 * i + 1 # left = 2*i + 1
right= 2 * i + 2 # right = 2*i + 2
# to verify the left child of root is greater than the root
if left< number and Ordering[i] < Ordering[left]:
largest = left
# to verify the right child of root is greaterightthan the root
if right< number and Ordering[largest] < Ordering[right]:
largest = right
# swap roots on neccesity
if largest != i:
Ordering[i],Ordering[largest] = Ordering[largest],Ordering[i] # swap
# Heapify the root.
heap_sort(Ordering, number, largest)
# main function for Ordering sorting
def heapSort(Ordering):
number = len(Ordering)
# max heap build process.
for i in range(number, -1, -1):
heap_sort(Ordering, number, i)
# extract of all the elements in the given heap
for i in range(number-1, 0, -1):
Ordering[i], Ordering[0] = Ordering[0], Ordering[i] # swap
heap_sort(Ordering, i, 0)
# main section of the code
Ordering = [ 12, 11, 13, 5, 6, 7 ,56 ,45 ,67 ,78 ,34 ,4 ,33]
heapSort(Ordering)
number = len(Ordering)
print ( "Sorted Ordering value is" )
for i in range( number):
print ( " %d " %Ordering[i])
Output:
6. Radix Sort
Radix sort is a sorting technique that progresses without comparing the elements keyed in. This is achieved by means of generating a bucket according to the radix value for elements with more than one digit involved; the technique is applied for all the digits in the element. It is also termed as bucket sort. This sorting technique tends to be too quick in their suitable environments.
Code:
def radix_sort(The_list, base=10):
if The_list == []:
return
def Input_factory(numeral, base):
def Input(The_list, index):
return ((The_list[index]//(base**numeral)) % base)
return Input
greatest = max(The_list)
exponent = 0
while base**exponent <= greatest:
The_list = sort_count(The_list, base - 1, Input_factory(exponent, base))
exponent = exponent + 1
return The_list
def sort_count(The_list, greatest, Input):
count = [0]*(greatest + 1)
for i in range(len(The_list)):
count[Input(The_list, i)] = count[Input(The_list, i)] + 1
# to determine the last index for each of the element
count[0] = count[0] - 1
# zero-based indexing decrement
for i in range(1, greatest + 1):
count[i] = count[i] + count[i - 1]
output_value = [None]*len(The_list)
for i in range(len(The_list) - 1, -1, -1):
output_value[count[Input(The_list, i)]] = The_list[i]
count[Input(The_list, i)] = count[Input(The_list, i)] - 1
return output_value
The_list = input('Enter the list of (nonnegative) numbers: ').split()
The_list = [int(x) for x in The_list]
sorted_list = radix_sort(The_list)
print( ' Radix oriented sorted output : ' , end='')
print(sorted_list)
Output:
Conclusion
Over a period of time, there were numerous algorithms designed for sorting the input set. They were designed with the motto of achieving better technique and optimized execution in the sorting process. Some of the most key ones are discussed above. From a python perspective, this language stands out to be a very flexible and steady language for getting these algorithms designed.
Recommended Articles
This is a Guide to Sorting Algorithms in Python. Here we discuss the introduction and top 6 sorting algorithms in python along with its code implementation. You may also look at the following articles to learn more-