Updated March 24, 2023
Introduction to Searching in Data Structure
Searching in data structure refers to the process of finding location LOC of an element in a list. This is one of the important parts of many data structures algorithms, as one operation can be performed on an element if and only if we find it. Various algorithms have been defined to find whether an element is present in the collection of items or not. This algorithm can be executed on both internal as well as external data structures. The efficiency of searching an element increases the efficiency of any algorithm.
Searching Techniques in Data Structure
The most famous techniques of searching in data structures are:
1. Sequential Search
This is the traditional technique for searching an element in a collection of elements. In this type of search, all the elements of the list are traversed one by one to find if the element is present in the list or not. One example of such an algorithm is a linear search. This is a straightforward and basic algorithm. Suppose ARR is an array of n elements, and we need to find location LOC of element ITEM in ARR. For this, LOC is assigned to -1, which indicates that ITEM is not present in ARR. While comparing ITEM with data at each ARR location, and once ITEM == ARR[N], LOC is updated with location N+1. Hence we found the ITEM in ARR.
Algorithm:
LSEARCH(ARR, N, ITEM, LOC) Here ARR Is the array of N number of elements, ITEM holds the value we need to search in the array and algorithm returns LOC, the location where ITEM is present in the ARR. Initially, we have to set LOC = -1.
1. Set LOC = -1,i=1
2. Repeat while DATA[i] != ITEM:
i=i+1
3. If i=N+1 ,then Set LOC =0
Else LOC = N+1
4. Exit.
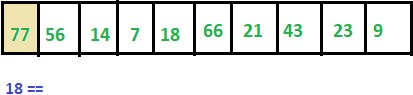
Let’s say, below is the ARR with 10 elements. And we need to find whether ITEM= 18 is present in this array or not.
In the start, LOC =-1
Step 1: ITEM != 77 thus we move to next element.
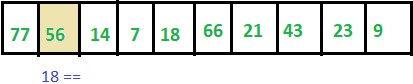
Step 2: ITEM != 56 thus we move to next element.
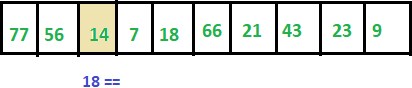
Step 3: ITEM != 14 thus we move to next element.
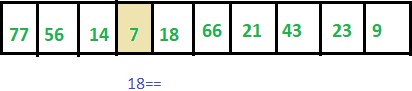
Step 4: ITEM != 7 thus we move to the next element.
Step 5: Hence ITEM == ARR[4] thus LOC updated to 5.
The complexity of Sequential Search
Here are the complexities of the linear search given below.
Space complexity
As linear search algorithm does not use any extra space, thus its space complexity = O(n) for an array of n number of elements.
Time Complexity
- Worst-case complexity: O(n) – This case occurs when the search element is not present in the array.
- Best case complexity: O(1) – This case occurs when the first element is the element to be searched.
- Average complexity: O(n) – This means when an element is present somewhere in the middle of the array.
2. Binary Search
This is a technique to search an element in the list using the divide and conquer technique. This type of technique is used in the case of sorted lists. Instead of searching an element one by one in the list, it directly goes to the middle element of the list, divides the array into 2 parts, and decides element lies in which sub-array the element exists.
Suppose ARR is an array with sorted n number of elements present in increasing order. With every step of this algorithm, the searching is confined within BEG and END, which are the beginning and ending index of sub-arrays. The index MID defines the middle index of the array where,
MID = INT(beg + end )/2
It needs to be checked if ITEM < ARR[N} where ITEM is the element that we need to search in ARR.
- If ITEM = ARR[MID] then LOC = MID and exit .
- If ITEM < ARR[MID} then ITEM can appear in the left sub-array, then BEG will be the same and END = MID -1 and repeat.
- If ITEM > ARR[MID] then ITEM can appear in the right subarray then BEG = MID+1 and END will be the same and repeat.
After this MID is again calculated for respective sub-arrays, if we didn’t find the ITEM, the algorithm returns -1 otherwise LOC = MID.
Algorithm:
BSEARCH(ARR, LB, UB, ITEM, LOC) Here, ARR is a sorted list of elements, with LB and UB are lower and upper bounds for the array. ITEM needs to be searched in the array and algorithm returns location LOC, index at which ITEM is present else return -1.
1. Set BEG = LB, END = UB and MID = INT([BEG+END]/2)
2. Repeat step 3 and 4 while BEG <= END and ARR[MID] != ITEM
3. IF ITEM< ARR[MID] then:
Set END = MID-1
Else:
Set BEG = MID+1
4. Set MID = INT(BEG+END)/2
5. IF ARR[MID] = ITEM then:
Set LOC = MID
Else:
Set LOC = NULL
6. Exit.
Let’s say here, ITEM = 62
BEG = 1 and END =9 Hence MID = (1+9)/2 = 5
ARR[MID] = 52
Step 1: ARR[MID] < ITEM : thus END =9 and BEG = MID +1 = 6. Thus our new sub-array is,
Step 2: Now BEG =6 and END =9 thus MID = INT([6+9]/2)= 6
NOW ARR[6] =ITEM. Thus LOC = MID
Thus LOC = 6
The complexity of Binary Search
Here are the complexities of the binary search given below.
- Worst Case: O(nlogn)
- Best Case: O(1)
- Average Case: O(nlogn)
Conclusion
Searching refers to finding the location of one element in the array of n elements. There are 2 types of search linear and binary Search, Linear search algorithm is straightforward and has O(n) of complexity whereas Binary Search is a high-speed searching algorithm having the complexity of (logn) but can only be used in case of the sorted list of elements. In case the size of the array is large, it is preferable to use binary search instead of linear search. Binary search is used in many searching data structures. In the case of mid-size arrays, the linear search algorithm is more preferred.
Recommended Articles
This is a guide to Searching in Data Structure. Here we discuss the techniques of searching in a data structure along with its algorithm and implementation. You can also go through our suggested articles to learn more –