Introduction to Banker’s Algorithm in C

Banker’s Algorithm in C is simple to implement deadlock avoidance and resource allocation algorithm. It executes all the available processes per the resources required to execute efficiently, avoiding deadlock. This algorithm checks if the safe state exists or not. The key concepts of a banker’s algorithm will be covered in this article, and you can use it in the real world.

Introduction to Banker’s Algorithm in C

Key Takeaways

The Banker’s Algorithm functions as a Deadlock Avoidance and Deadlock Detection algorithm.
It assesses the system’s safety by computing the Allocation of maximum potential resources.
Due to a fixed number of processes, its applicability to interactive systems is limited. Therefore, a dynamic system is essential to meet the algorithm’s requirements, ensuring its effectiveness in managing resources and preventing deadlocks.

Why is it called the Banker Algorithm?

Banker’s Algorithm in C avoids deadlock situations. It is named the banker’s algorithm because of its primary use in the banking sector for deciding whether or not to approve a loan to an individual.

For example, a bank has “n” number of account holders, and the total amount of money in all accounts is “s.” Once the bank allocates a loan, the amount is subtracted from the total “s.” This algorithm checks if the difference is greater than the amount “s.” It is to ensure the bank has enough money if all the “n” account holders draw their money simultaneously.

Let us suppose That Mr. Maliya asks ABC Bank for a big loan of 200 Crore. The bank needs to check if it has enough money to give him the loan without going broke.

So, ABC Bank looks at all the money it has from everyone’s accounts (total balance). If this total money is more than 200 Crore, great! The bank can give Mr. Maliya the loan. But if the total money is less than 200 Crore, the bank can’t afford to give him the loan because it would run out of money.

This way, ABC Bank makes sure it only gives out loans it can cover with its money. It’s like checking if you have enough money in your piggy bank before promising to give some to a friend.

Working of the Banking Algorithm

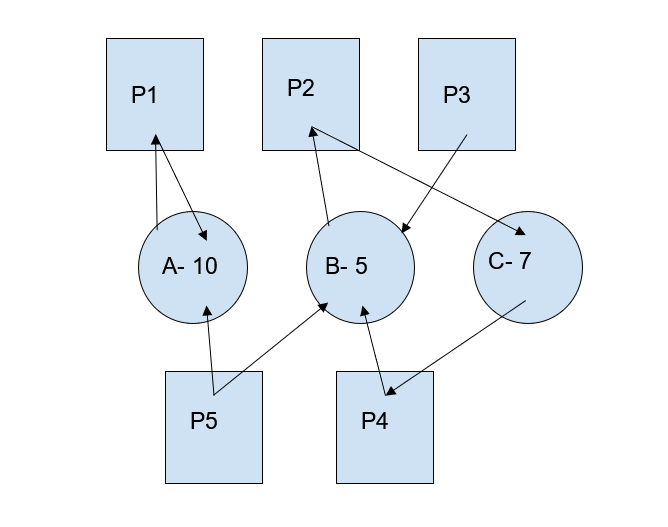
Suppose we have five processes, P1, P2, P3, P4, and P5, and resources A, B, and C to be allocated to each process. We are aware of their maximum need. In this case, we need to implement the Banker’s algorithm to determine the remaining need and find a sequence of processes, ensuring a safe state. The total resources available are A=10, B=5, and C=7.

Now, we will see how this algorithm works efficiently in finding the available resources. Here, Remaining need = (Max need- Allocation)

Processes	Allocation	Max Need	Available	Remaining need
Processes	ABC	ABC	ABC	ABC
P1	010	753	–	743
P2	200	312	–	112
P3	302	802	–	500
P4	211	222	–	011
P5	002	533	–	531

Now, we will check the available resources. Available resources = (Total – Allocation).

For A, Total= [0+2+3+2+0]=7 Available= [10-7]=3 For B, Total= [1+0+0+1+0]=2 Available= [5-2]=3 For C, Total= [0+0+2+1+2]=5 Available= [7-5]=2

1st Iteration:

Processes	Allocation	Max Need	Available	Remaining need
Processes	ABC	ABC	ABC	ABC
P1	010	753	332	743
P2	200	312	–	112
P3	302	802	–	500
P4	211	222	–	011
P5	002	533	–	531

Now, we have available resources (332). We will check which process can use this resource. Now, compare the remaining needs with the available resources. P2 needs 112, and the available resources are 332, which means the P2 process can use these resources.

Find what is newly available from P2 and perform the above steps again. new available= allocation of P2+ available (2+3),(0+3),(0+2)=[ 5, 3, 2 ]

2nd Iteration:

Processes	Allocation	Max Need	Available	Remaining need
Processes	ABC	ABC	ABC	ABC
P1	010	753	332	743
P2	200	312	532	112
P3	302	802	–	500
P4	211	222	–	011
P5	002	533	–	531

Now, P3 needs 500, and the available resources are -532. So, the P3 process can use these resources. And the sequence will be <P2, P3>.

Now available using P3= (5+3),(3+0),(2+2)=8,3,4

3rd Iteration:

Processes	Allocation	Max Need	Available	Remaining need
Processes	ABC	ABC	ABC	ABC
P1	010	753	332	743
P2	200	312	532	112
P3	302	802	834	500
P4	211	222	–	011
P5	002	533	–	531

Now, P5 needs 5, 3, 1, and available are 834, so P5 can utilize the resources.

Add P5 to the sequence < P2, P3, P5 >

Now available using P5= (8+0), (3+0), (4+2)= 836

4th Iteration:

Processes	Allocation	Max Need	Available	Remaining need
Processes	ABC	ABC	ABC	ABC
P1	010	753	332	743
P2	200	312	532	112
P3	302	802	834	500
P4	211	222	836	011
P5	002	533	–	531

P1 needs 7,4,3, and we have 836 resources. Hence, P1 can use the resources.

Add P1 to the sequence. < P2, P3, P5, P1 >

Now available using P1=(8+0), (3+1), (6+0)= 846

5th Iteration:

Processes	Allocation	Max Need	Available	Remaining need
Processes	ABC	ABC	ABC	ABC
P1	010	753	332	743
P2	200	312	532	112
P3	302	802	834	500
P4	211	222	836	011
P5	002	533	846	531

Now, P4 needs 011, and we have 846 resources. P4 can use these resources.

Hence the order is << P2, P3, P5, P1, P4 >

Banker’s algorithm will allocate the resources to different processes in such a manner that there will be no deadlock situation in terms of resource crunch. In the above scenario, the best sequence to allocate resources is- < P2, P3, P5, P1, P4 >

The data structure used Implements the Banker Algorithm

The data structures utilized for implementing the Banker’s Algorithm include.

1. Available Array

This array, with a length of m, signifies the available resources of each type.

If Available[j] = k, it denotes the presence of k instances for resource type Rj.

2. Max Matrix

An n x m matrix represents the maximum instances each process can request for each resource.

If Max[i][j] = k, process Pi can request up to k instances of resource type Rj.

3. Allocation Matrix

An n x m matrix reveals the current Allocation of resources to each process.

If Allocation [i][j] = k, it indicates that procedure At the moment, k instances of resource type Rj are assigned to Pi.

4. Need Matrix

A two-dimensional array, n x m, showcases each process’s remaining resource needs. If Need[i][j] = k, it implies that process Pi might require k more instances of resource type Rj to complete its task.

Banker’s Algorithm in C: Types

The Banker’s Algorithm comprises two distinct components.

1. Safety Test Algorithm

This algorithm will check if granting the request will ensure a safe state. If the process can find a safe sequence, the request is granted; otherwise, it is denied. This algorithm helps ensure that resources are allocated in a way that avoids deadlock and guarantees the system’s safety. It is an important part of resource management in operating systems and banking systems to maintain system integrity and prevent resource-related issues.

1) Suppose Work and Finish are vectors of size ‘m’ and ‘n.’

Initialize: Work = Available

Finish[i] = false; for i=1, 2,…n

2) Find i such that

Finish[i] = false
Need [i] <= Work

if no such i exists

goto step (4)

3) Work = Work + Allocation[i]

Finish[i] = true

goto step (2)

4) for all i, if Finish [i] = true

the system is in a safe state

For example-

Available resources A = 4, B = 2, C = 3

Request- 011

Processes	Allocation	Max Need	Work	Remaining need
Processes	ABC	ABC	ABC	ABC
P1	112	214	535	102
P2	021	132	556	111
P3	100	521	–	421

Step 1- Initialization

Work = Available = [4 2 3]

Finish = [false false false]

Iteration 1-

Process 1: Need[1] = Max[1] – Alloc[1] = [1 0 2] <= Work (True)

Work = Work + Alloc[1] = [5 3 5]

Set Finish[1] to true.

Iteration 2-

Process 2: Need[2] = Max[2] – Alloc[2] = [1 1 1] <= Work (True)

Work = Work + Alloc[2] = [5 5 6]

Set Finish[2] to true.

Iteration 3-

Process 3: Need[3] = Max[3] – Alloc[3] = [4 2 1] NOT <= Work (False)

No suitable process found; terminate.

Final Result:

Processes 1 and 2 finished successfully, and the system remains in a safe state. The request [0 1 1] can be granted. In the above example, we have a different initial state and a new resource request, showcasing how the Safety Test Algorithm ensures the system remains safe while processing resource requests.

2. Resource Request Handling Algorithm

In the Banker’s algorithm, the Resource Request Handling Algorithm handles the processes’ requests for additional resources. It determines whether granting the requested resources will maintain the system’s safe state or not. The safe state is one in which the system can always find a sequence to finish all processes without encountering a deadlock.

If a request cannot be immediately granted without impacting the system’s safety, the process of requesting resources will have to wait until the requested resources are safe to allocate.

The Banker’s algorithm assumes that each process specifies its maximum resource needs upfront, making it easier to allocate resources and preventing deadlock situations.

Suppose a vector Request for Process Pi.

Requesti[j]= k means process Pi requires k instances of Resource Rj.

1) If Request[i] <= Need[i]

Goto step (2) ;

else

raise error condition as the process exceeds its maximum claim.

2) If Request[i] <= Available

Goto step (3);

else wait as the resources are not available.

3) Pretend to have allocated the resources that are requested to process Pi by modifying the state as

Available = Available – Request[i]

Allocation[i] = Allocation[i] + Request[i]

Need[i] = Need[i]– Request[i]

Note: A state is deemed Safe when all processes can execute without causing deadlocks. Conversely, an unsafe state implies processes cannot be completed safely

Implementation in C

#include 
#include 
int main() {
    int k=0,a=0,b=0,instance[5],availability[5],allocated[10][5],need[10][5],MAX[10][5],process,P[10],no_of_resources, cnt=0,i, j,op[10];
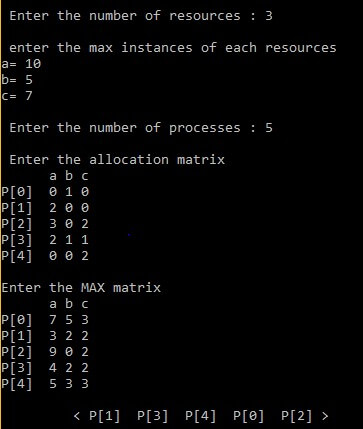
	printf("\n Enter the number of resources : ");
	scanf("%d", &no_of_resources);
	printf("\n enter the max instances of each resources\n");
	for (i=0;i<no_of_resources;i++) {
		availability[i]=0;
		printf("%c= ",(i+97));
		scanf("%d",&instance[i]);
	}
	printf("\n Enter the number of processes : ");
	scanf("%d", &process);
	printf("\n Enter the allocation matrix \n     ");
	for (i=0;i<no_of_resources;i++)
	printf(" %c",(i+97));
	printf("\n");
	for (i=0;i <process;i++) {
		P[i]=i;
		printf("P[%d]  ",P[i]);
		for (j=0;j<no_of_resources;j++) {
			scanf("%d",&allocated[i][j]);
			availability[j]+=allocated[i][j];
		}
	}
	printf("\nEnter the MAX matrix \n     ");
	for (i=0;i<no_of_resources;i++) {
		printf(" %c",(i+97));
		availability[i]=instance[i]-availability[i];
	}
	printf("\n");
	for (i=0;i <process;i++) {
		printf("P[%d]  ",i);
		for (j=0;j<no_of_resources;j++)
		 scanf("%d", &MAX[i][j]);
	}
	printf("\n");
	A: a=-1;
	for (i=0;i <process;i++) {
		cnt=0;
		b=P[i];
		for (j=0;j<no_of_resources;j++) {
			need[b][j] = MAX[b][j]-allocated[b][j];
			if(need[b][j]<=availability[j])
			 cnt++;
		}
		if(cnt==no_of_resources) {
			op[k++	]=P[i];
			for (j=0;j<no_of_resources;j++)
			availability[j]+=allocated[b][j];
		} else
		 P[++a]=P[i];
	}
	if(a!=-1) {
		process=a+1;
		goto A;
	}
	printf("\t <");
	for (i=0;i<k;i++) printf(" P[%d] ",op[i]); printf(">");
	getch();
}

Output

Real-life Example

Consider a multi-user operating system where multiple users or processes run simultaneously and compete for shared resources such as CPU time, memory, and printers. In such an environment, efficient resource allocation is crucial to ensure that each user or process can perform its tasks without getting stuck in a deadlock situation.

How Banker’s Algorithm Prevents Deadlocks and Ensures Efficient Resource Allocation:

1. Resource Management:

The Banker’s Algorithm manages and allocates resources in this multi-user computer system. Each process or user is required to declare its maximum resource needs upfront, including the maximum number of CPU cycles, memory, and printer access it may require during its execution.

2. Resource Request Handling:

When a process requests additional resources, the Banker’s Algorithm assesses whether granting these resources would maintain a safe state. It checks if the requested resources are available and if allocating them would avoid a potential deadlock.

3. Preventing Deadlocks:

The Banker’s Algorithm’s primary goal is to prevent deadlocks. It does so by ensuring that at any given time, resources are allocated in a way that allows the system to find a safe sequence to complete all processes.

If a user or process requests resources and granting those resources would lead to a safe state, the request is approved.
Suppose the requested resource allocation would potentially result in a deadlock (i.e., no safe sequence is possible). In that case, the request is denied, and the process is put in a waiting state until the resources become available.

4. Efficient Resource Utilization:

The Banker’s Algorithm also promotes efficient resource utilization. Once a process completes its tasks and releases the allocated resources, those resources become available for other processes. This ensures that resources are continuously used to their fullest extent, maximizing system efficiency.

Advantages and Disadvantages of Bankers Algorithm

Advantages

The Banker’s Algorithm offers several benefits.

The algorithm’s consideration of maximum resource requirements allows processes to utilize available resources to their fullest extent.
It facilitates the effective management of diverse resource types within the operating system.
The algorithm ensures continuous availability of resources that can fulfill the requirements of at least one process.
Upon completion, the process releases all the allocated resources, promoting efficient resource utilization.

Disadvantages

Despite its merits, the Banker’s Algorithm comes with some drawbacks.

Processes need to be aware of their maximum resource requirements, introducing a potential limitation.
Once a process begins execution, it cannot alter its resource needs, potentially leading to inefficiencies.
The algorithm lacks flexibility in accommodating new processes during ongoing execution.

Testing and Validation

Testing confirms that the information is accurate and reliable. However, the algorithm is designed to manage resource allocation and prevent deadlocks. Thorough testing identifies and rectifies potential issues before deploying the system in a real-world environment. It ensures that the algorithm performs as expected, even in scenarios with multiple processes, resource requests, and dynamic changes.

Below is the test case.

Processes	Allocation	Max Need	Work	Remaining need
Processes	ABC	ABC	ABC	ABC
P1	010	743	342	733
P2	200	322	542	122
P3	302	902	753	600
P4	211	222	755	011
P5	002	433	757	531

To validate the above test case, we can follow the below process.

Run the Resource Request Handling Algorithm using the provided test case.
Confirm that the algorithm accurately evaluates the request’s validity, verifies the availability of resources, and determines whether approving the request would maintain a safe state.
Verify the resulting system state after handling the request, ensuring that the Allocation and availability of resources are updated correctly.

Edge Cases and Impact on Algorithm

Edge Case 1- Invalid Request

Evaluate how the algorithm handles requests surpassing a process’s maximum declared resource demand, ensuring it accurately denies such requests.

Impact- If the algorithm fails to deny requests exceeding the maximum declared demand for a resource, it risks resource over-allocation. This could lead to unsafe states, compromising system stability and potentially causing deadlock or resource contention issues.

Edge Case 2- Insufficient Resources

Evaluate the algorithm’s response when a process requests resources beyond the available capacity. Ensure the algorithm properly orchestrates a wait for the process until the required resources become available.

Impact- Inadequate handling of requests when insufficient resources may result in improper Allocation. Failure to ensure processes wait for required resources can lead to execution with insufficient resources, jeopardizing system stability and increasing the risk of deadlock.

Edge Case 3- Deadlock Avoidance

Assess the algorithm’s effectiveness in preventing deadlock situations. Test with multiple processes making requests and confirm that the system remains safe throughout.

Impact- The algorithm’s effectiveness in preventing deadlock situations is critical. If it struggles to maintain a safe state during multiple processes making requests, the risk of deadlocks increases. Deadlocks halt processes, waste resources, and negatively impact system performance, posing a significant threat to overall system reliability.

Complexity of the Banker Algorithm

The complexity of the Banker’s Algorithm depends on many factors, such as the number of processes and resources and the existing state of the system.

Time Complexity: O(n * m^2)

The time complexity of the Banker’s Algorithm O(n * m^2).

Where n represents the number of processes and m is the number of resource types.

Space Complexity: O(n * m)

The space complexity of the Banker’s Algorithm O(n).

Where n is the quantity of processes and m is the number of resource types.

Conclusion

The Banker’s Algorithm in C serves as a deadlock avoidance method, comprising essential components like the safety and resource request algorithms. Its primary goal is to allocate resources to processes while preventing unsafe states. However, practical implementation faces challenges, as accurately determining a process’s resource requirements in advance is often impractical. This limitation makes the full implementation of the Banker’s Algorithm unfeasible in real-world scenarios.

Frequently Asked Questions (FAQs)

Q1. Can the Banker’s Algorithm handle dynamic changes in resource needs during the execution of a process?

Answers: No, the Banker’s Algorithm does not accommodate dynamic changes in a process’s resource needs once it has begun execution. The maximum resource requirements must be declared upfront, and any alterations during processing are not allowed.

Q2 .What happens when a process finishes its task in the Banker’s Algorithm?

Answers: When a process is done with its job, it returns the resources it used. The algorithm then adjusts the available resources and the allocation matrix. This helps make sure that resources become available for other tasks, keeping the system ready to handle future requests safely.

Q3. In what real-world scenarios is the Banker’s Algorithm practically challenging to implement?

Answers: The Banker’s Algorithm faces practical challenges in scenarios where predicting the exact resource needs of a process in advance is difficult. For instance, in dynamic environments or unpredictable workloads, accurately determining the maximum resource requirements becomes impractical, limiting the algorithm’s feasibility.

Quiz Result
Total Questions	Correct Answers	Wrong Answers	Percentage