Updated April 10, 2023
Introduction to DFS Algorithm in C
DFS Algorithm in C is a Graph Traversal Technique, also known as Depth first Search Algorithm, where user traverses with initial node of the graph, and then gets deeper until user finds the required node or node which has no children. Depth First Search can be used to search in Tree or Graph. Traversals of both Graph and Tree are almost similar but the only catch is that Graphs contains cycles and nodes, and node can be visited twice. DFS uses stack as a data structure and process or algorithm is similar to BFS algorithm. In DFS, edges which leads user to unvisited nodes are known as discovery edges and edges which lead to already visited node are called block nodes. In this article, we shall learn what is DFS Algorithm and How is it implemented in one of the known programming languages. i.e. C
Syntax:
DFS does not have a Syntax but has Algorithm or Steps which can be used to perform Depth First Search Algorithm.
Algorithm of DFS in C
- Step 1: One of the standard rule before starting with DFS algorithm is that DFS puts each vertex of graph into two categories i.e. Visited & Non Visited.
- Step 2: Keeping in mind that each vertex is visited at least once without making cycles.
- Step 3: First, need to put any one graph vertices on top of the stack
- Step 4: Need to take a top item of the stack and get it added to the visited list
- Step 5: Then, create a list of vertex adjacent nodes and add the ones which are not in the visited list to the top of the stack
- Step 6: Just keep repeating the above step 4 & step 5 until the stack gets emptied.
DFS employs some major rules for traversal,
- Rule 1: Visit adjacent unvisited vertex and mark it as Visited. Display and push it to a stack
- Rule 2: If there is no adjacent vertex found, remove vertex from the top of the stack. It will remove all the vertices from the stack which has no adjacent vertices.
- Rule 3: Keep on repeating Rule 1 and Rule 2 until the stack is emptied.
How does DFS Work in C?
Let’s see how does DFS actually work with some examples,
Example #1 – C Program to Implement DFS Algorithm
Code:
#include <stdio.h>
#include <stdlib.h>
intsourceV,Vertex,Edge,time,visited[10],Graph[10][10];
void DepthFirstSearch(inti)
{
int j;
visited[i]=1;
printf(" %d->",i++);
for(j=0;j<Vertex;j++)
{
if(Graph[i][j]==1&&visited[j]==0)
DepthFirstSearch(j);
}
}
intmain()
{
inti,j,vertex1,vertex2;
printf("\t\t\tGraphs\n");
printf("Enter no. of edges:");
scanf("%d",&Edge);
printf("Enter no. of vertices:");
scanf("%d",&Vertex);
for(i=0;i<Vertex;i++)
{
for(j=0;j<Vertex;j++)
Graph[i][j]=0;
}
for(i=0;i<Edge;i++)
{
printf("Enter the edges in V1 V2 : ");
scanf("%d%d",&vertex1,&vertex2);
Graph[vertex1-1][vertex2-1]=1;
}
for(i=0;i<Vertex;i++)
{
for(j=0;j<Vertex;j++)
printf(" %d ",Graph[i][j]);
printf("\n");
}
printf("Enter source Vertex: ");
scanf("%d",&sourceV);
DepthFirstSearch(sourceV-1);
return 0;
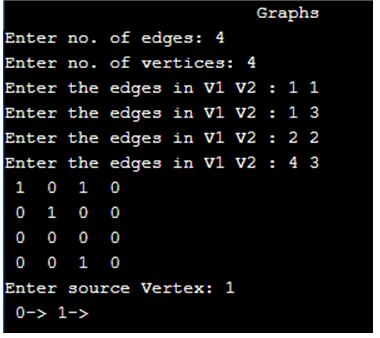
}Output 1:
So here in this output, No. of edges being 4 and vertices also being 4. According to the vertice, Graph traversal has been shown.
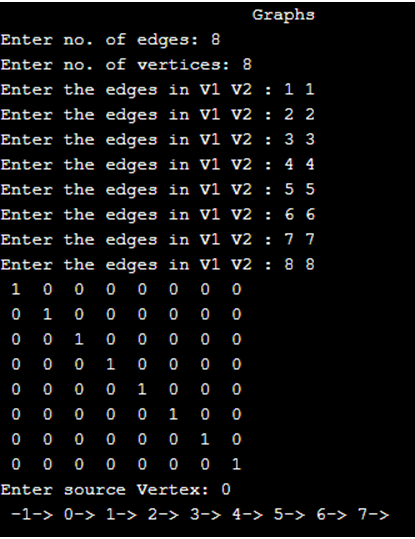
Output 2: No. of edges = No. of Vertices = 8
Example #2 – DFS Example for Graph Traversal
Code:
/******************************************************************************
Online C Compiler.
Code, Compile, Run and Debug C program online.
Write your code in this editor and press "Run" button to compile and execute it.
*******************************************************************************/
#include<stdio.h>
#include<stdlib.h>
#define MAXVALUE 100
#define initialValue 1
#define visitedValue 2
int node;
int adjacent[MAXVALUE][MAXVALUE];
int state[MAXVALUE];
void DFSTraversal();
void DFS(int vertex);
void createGraph();
int stack[MAXVALUE];
inttopValue = -1;
void pushNode(int vertex);
intpopNode();
intisEmpty();
main()
{
createGraph();
DFSTraversal();
}
void DFSTraversal()
{
int vertex;
for(vertex=0; vertex<node; vertex++)
state[vertex]=initialValue;
printf("\nEnter start node for DFS : ");
scanf("%d",&vertex);
DFS(vertex);
printf("\n");
}
void DFS(int vertex)
{
inti;
pushNode(vertex);
while(!isEmpty())
{
vertex = popNode();
if(state[vertex]==initialValue)
{
printf("%d ",vertex);
state[vertex]=visitedValue;
}
for(i=node-1; i>=0; i--)
{
if(adjacent[vertex][i]==1 && state[i]==initialValue)
pushNode(i);
}
}
}
void pushNode(int vertex)
{
if(topValue == (MAXVALUE-1)){
printf("\n Error: Stack Overflow\n");
return;
}
topValue=topValue+1;
stack[topValue] = vertex;
}
intpopNode()
{
int vertex;
if(topValue == -1)
{
printf("\nStack Underflow\n");
exit(1);
}
else
{
vertex = stack[topValue];
topValue=topValue-1;
return vertex;
}
}
intisEmpty( )
{
if(topValue == -1)
return 1;
else
return 0;
}
void createGraph()
{
inti,maxEdges,originNode,destinNode;
printf("\nEnter number of nodes : ");
scanf("%d",&node);
maxEdges=node*(node-1);
for(i=1;i<=maxEdges;i++)
{
printf("\nEnter edge %d( -3 -3 to quit ) : ",i);
scanf("%d %d",&originNode,&destinNode);
if( (originNode == -3) && (destinNode == -3) )
break;
if( originNode>= node || destinNode>= node || originNode<0 || destinNode<0)
{
printf("\nInvalid Edge/ Node!\n");
i--;
}
else
{
adjacent[originNode][destinNode] = 1;
}
}
}Output:
With this, we shall conclude the article ‘DFS Algorithm in C’. We have seen what DFS Algorithm is all about and have also gone through algorithm steps. Worked on 2 of the examples listed above which are helpful to understand the DFS Algorithm technically and programmatically. This DFS algorithm is applicable in many ways, such as, To find path, to test if graph is bipartite, detecting cycles in graph and to strongly finding connected components of the graph, etc. There is time complexity determined which is represented in the form of 0(V + E), where V represents No. of Nodes and E represents No. of Edges. Hence Space Complexity of the Algorithm is 0(V).
Recommended Articles
This is a guide to DFS Algorithm in C. Here we also discuss the introduction and how does DFS actually work along with different examples and its code implementation. You may also have a look at the following articles to learn more –