Updated July 28, 2023
Weighted Mean Formula (Table of Contents)
- Weighted Mean Formula
- Examples of Weighted Mean Formula (With Excel Template)
- Weighted Mean Formula Calculator
Weighted Mean Formula
Mean is a point in a data set which is the average of all the data point we have in a set. It is simply calculated by taking a sum of all the data points and dividing by a number of data points.
So basically all the data points are given equal weights when we calculated the simple mean. Weighted Mean is the average of data set which is calculated by giving different weights different data points. This assignment of different weights gives us the flexibility to assign more power to the more relevant data point and less power to a less relevant data point. But weighted mean will be equal to the arithmetic mean if all the weights are equal.
Let us say that we have a data set X with n data points and is given by X {X1, X2, X3………..Xn}. So the formula for simple mean is simply given by:
In another way:
So all the data points have the same weight and are given by 1/n.
But let’s say weights are different and are given by {w1,w2, w3…………,wn}. So the formula for Weighted Mean is given by:
Examples of Weighted Mean Formula (With Excel Template)
Let’s take an example to understand the calculation of Weighted Mean formula in a better manner.
Weighted Mean Formula – Example #1
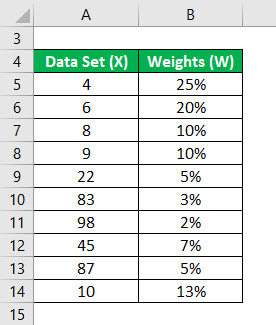
Let say you have a data set with 10 data points and we want to calculate the weighted mean for that.
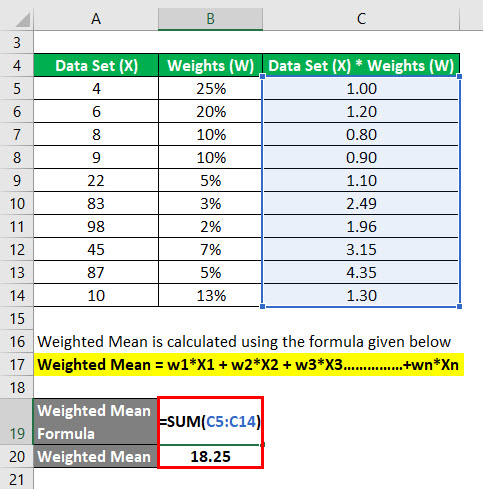
Data set : {4, 6, 8, 9, 22, 83, 98, 45, 87, 10}
Weights : {20%, 15%, 10%, 10%, 5%, 3%, 2%, 7%, 5%, 13%}
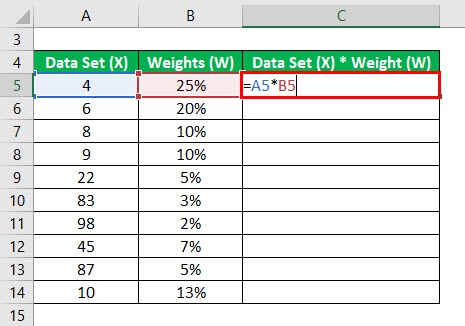
First, we calculate the product of data set and weights.
The result will be as given below.
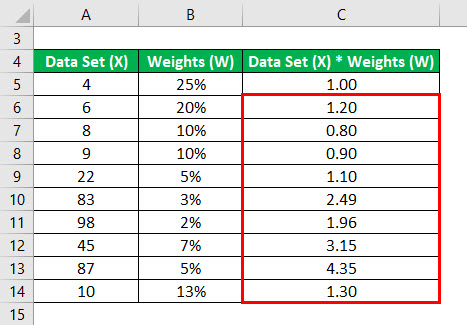
Similarly, We have calculated for all the data.
Weighted Mean is calculated using the formula given below
Weighted Mean = w1*X1 + w2*X2 + w3*X3……………+wn*Xn
- Weighted Mean = (4 * 25%) + (6 * 20%) + (8 * 10%) + (9 * 10%) + (22 * 5%) + (83 * 3%) + (98 * 2%) + (45 * 7%) + (87 * 5%) + (10 * 13%)
- Weighted Mean = 18.25
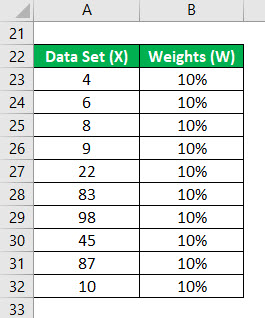
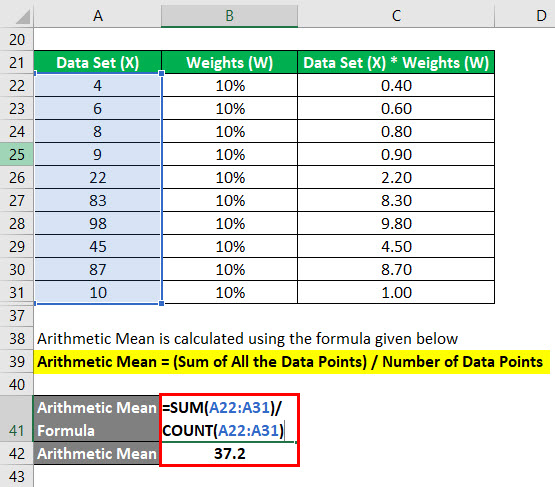
Let’s say all the weights are equal i.e 10% for each data set.
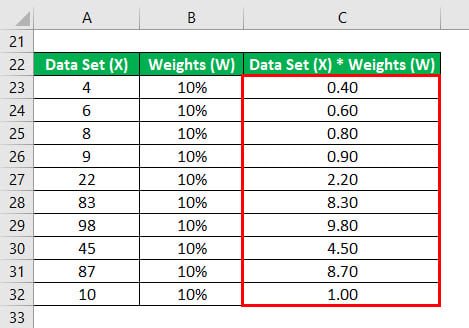
First, we calculate the product of data set and weights.
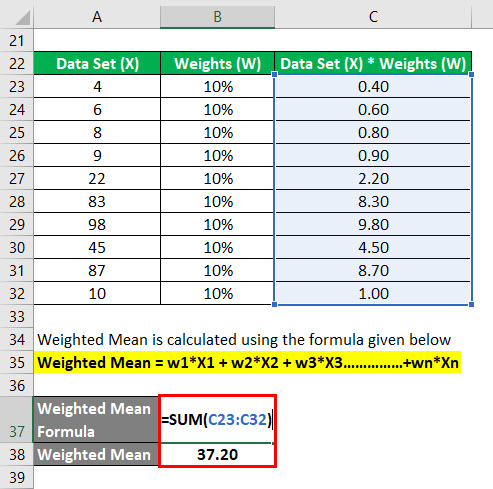
Weighted Mean is calculated using the formula given below
Weighted Mean = w1*X1 + w2*X2 + w3*X3……………+wn*Xn
- Weighted Mean = (4 * 10%) + (6 * 10%) + (8 * 10%) + (9 * 10%) + (22 * 10%) + (83 * 10%) + (98 * 10%) + (45 * 10%) + (87 * 10%) + (10 * 10%)
- Weighted Mean = 37.20
Arithmetic Mean is calculated using the formula given below
Arithmetic Mean = (Sum of All the Data Points) / Number of Data Points
- Arithmetic Mean = (4+6+8+9+22+83+98+45+87+10) /10
- Arithmetic Mean =37.2
So when all the weights are equal, arithmetic mean is same as weighted mean
Weighted Mean Formula – Example #2
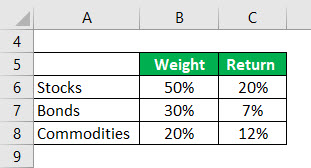
Let’s say you have a portfolio in which you have stocks, bonds, and commodities. So basically we have a portfolio in which we have invested in stocks, bonds, and commodities. Following are the weights /proportions of each of the instrument have in your portfolio:
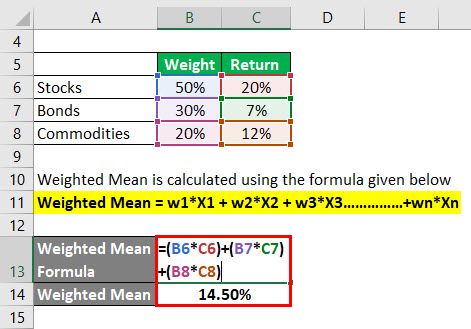
Weighted Mean is calculated using the formula given below
Weighted Mean = w1*X1 + w2*X2 + w3*X3……………+wn*Xn
- Weighted Mean = 50% * 20% + 30% * 7% + 20% * 12%
- Weighted Mean = 14.5%
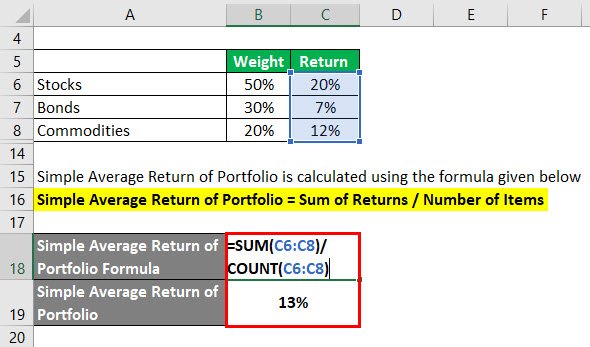
Simple Average Return of Portfolio is calculated using the formula given below
Simple Average Return of Portfolio = Sum of Returns / Number of Items
- Simple Average Return of Portfolio = (20% + 7% + 12%) / 3
- Simple Average Return of Portfolio = 13%
So if you see here, since stocks have given more weight and they have generated a higher return, a weighted return is more than the simple return.
Explanation
Weighed mean is basically the average of the data points calculated along with associated weights with them. It is not necessary that always all the data points have the same relevance, so only calculating simple is not enough then. That is the reason that weighted mean has much more practical relevance than the simple mean. For example, We know that students have to face various types of exams and have to submit different assignments. All those exams and assignments have different weightage given to them. Assignment 1: 10%, Assignment 2: 10%, Assignment 3: 20%, Final exam: 60%. So if a student has not performed well in all the three assignments, he can prepare well to score well in the final exam so that his average score moves up.
The simple mean value is easily distorted by extreme values/outliers. So weighted mean is the correct way to find the average of data set. So if there is an extreme value which has very less relevance, it will not impact the average significantly. Similarly, if there is an extreme value and it has much relevance, its impact should be visible in the average value.
Relevance and Uses of Weighted Mean Formula
Mean is very simple yet one of the crucial elements of statistics. It is the basic foundation of statistical analysis of data. But in real and practical life, arithmetic mean is just a theoretical concept which forms the basis for more relevant tool i.e. weighted mean. Weighted mean has so many practical applications like calculating the average return of the portfolio, calculating average grades in examinations, finding the cost of capital in capital projects (WACC), finding the inventory value at end of the period when prices are changing, etc. So basically weighted mean overcome the issues which simple mean has and is more relevant. The simple fact is that it makes sense. Having the same weights for all the elements in a data set is not practical. For example inventory in the company is purchased at different prices, so simple means will not give accurate inventory value at the end of the period. Or in capital projects, the company can have a different source of funds like debt, equity etc.so simply taking the mean value of all the cost is not the right way. The weighted mean is more practical and more relevant.
Weighted Mean Formula Calculator
You can use the following Weighted Mean Calculator
| w1 | |
| X1 | |
| w2 | |
| X2 | |
| w3 | |
| X3 | |
| w4 | |
| X4 | |
| Weighted Mean Formula | |
| Weighted Mean Formula = | w1*X1 + w2*X2 + w3*X3 + w4*X4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Recommended Articles
This has been a guide to Weighted Mean formula. Here we discuss how to calculate the Weighted Mean along with practical examples. We also provide a Weighted Mean calculator with downloadable excel template. You may also look at the following articles to learn more –