Updated July 28, 2023
Outliers Formula (Table of Contents)
Outliers Formula
The extremely high value and extremely low values are the outlier values of a data set. This is very useful in finding any flaw or mistake that occurred. Simply as the name says, Outliers are values that lied outside from the rest of the values in the data set.
Example, consider engineering students and imagine they had dwarves in their class. So dwarves are the people who are extremely low in height when compared with other normal heighted people. So this is the outlier value in this class. Outlier values can be calculated using the Tukey method.
The formula for Outliers –
Higher Outlier= Q3 + (1.5 * IQR)
Examples of Outliers Formula (With Excel Template)
Let’s take an example to understand the calculation of Outliers formula in a better manner.
Outliers Formula – Example #1
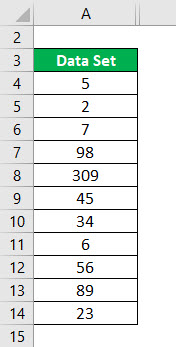
Consider the following data set and calculate the outliers for data set.
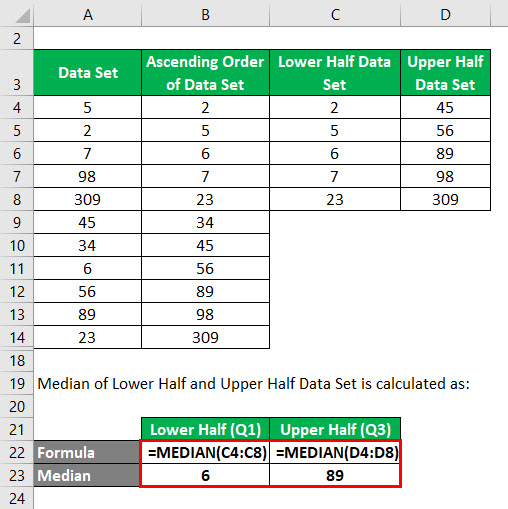
Data Set = 5, 2, 7, 98, 309, 45, 34, 6, 56, 89, 23
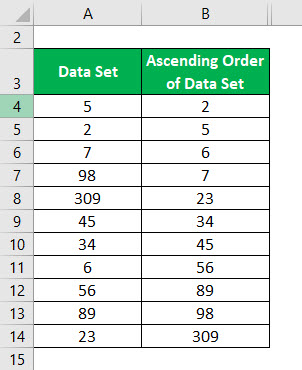
Ascending Order of Data Set:
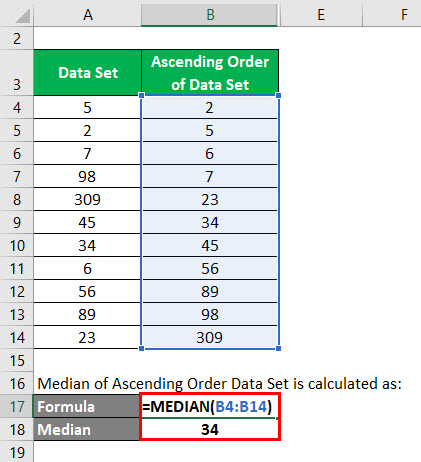
Median of Ascending Order Data Set is calculated as:
In this data set, the total number of data is 11. So n= 11. Median = 11+1/2 = 12 / 2 = 6. Hence the value which is in 6th position in this data set is the median.
So Median value = 34.
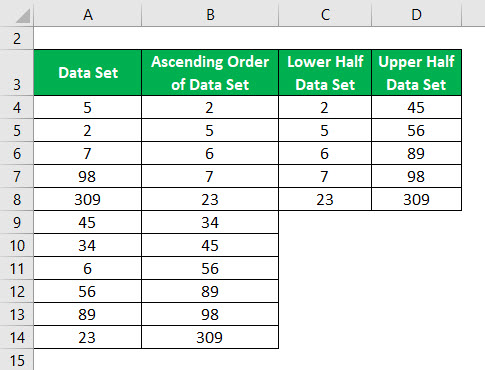
Split the Data Set into 2 halves using the median.
Median of Lower Half and Upper Half Data Set is calculated as:
- In the lower half 2, 5, 6,7,23, if we find the median like how we found in step 2, the median value would be 6. So Q1= 6.
- In the Upper half 45, 56, 89, 98,309 if we find the median like how we found in step 2, the median value would be 89. So Q3= 89.
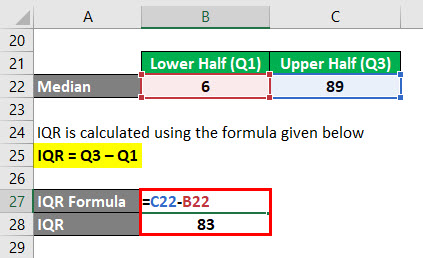
IQR is calculated using the formula given below
IQR = Q3 – Q1
- IQR = 89 -6
- IQR = 83
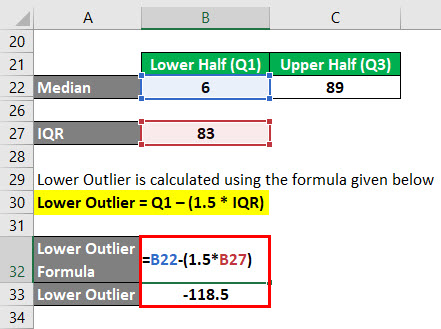
Lower Outlier is calculated using the formula given below
Lower Outlier = Q1 – (1.5 * IQR)
- Lower Outlier = 6 – (1.5 * 83)
- Lower Outlier = -118.5
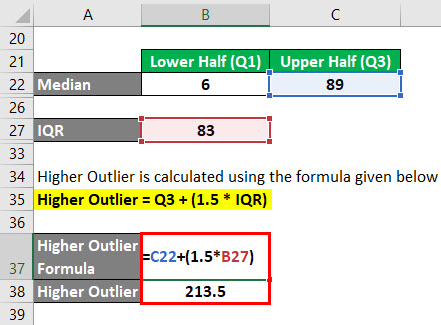
Higher Outlier is calculated using the formula given below
Higher Outlier = Q3 + (1.5 * IQR)
- Higher Outlier = 89 + (1.5 * 83)
- Higher Outlier = 213.5
Now fetch these values in the data set -118.5, 2, 5, 6, 7, 23, 34, 45, 56, 89, 98, 213.5, 309. Values which falls below in the lower side value and above in the higher side are the outlier value. For this data set, 309 is the outlier.
Outliers Formula – Example #2
Consider the following data set and calculate the outliers for data set.
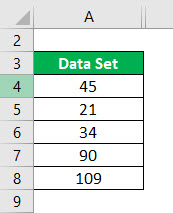
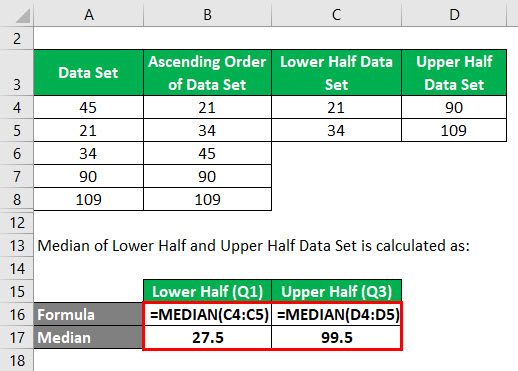
Data Set = 45, 21, 34, 90, 109.
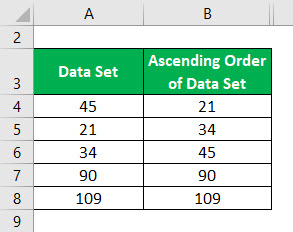
Ascending Order of Data Set:
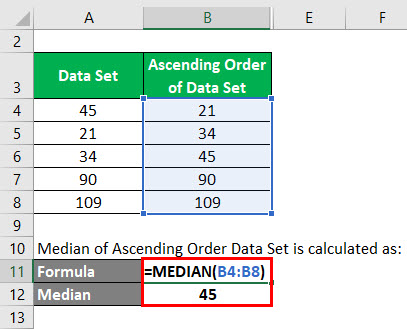
Median of Ascending Order Data Set is calculated as:
In this data set, the total number of data is 5. So n = 5. Median = 5+1/2 = 6 / 2 = 3. Hence the value which is in 3rd position in this data set is the median.
So Median value = 45.
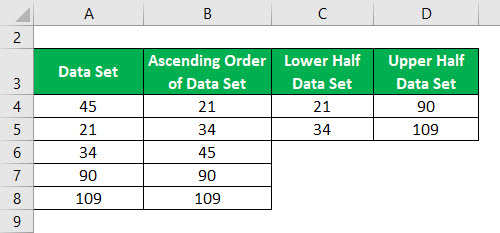
Split the Data Set into 2 halves using the median.
Median of Lower Half and Upper Half Data Set is calculated as:
- Q1= 27.5
- Q3= 89
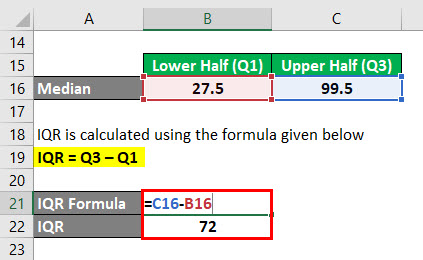
IQR is calculated using the formula given below
IQR = Q3 – Q1
- IQR = 99.5 – 27.5
- IQR = 72
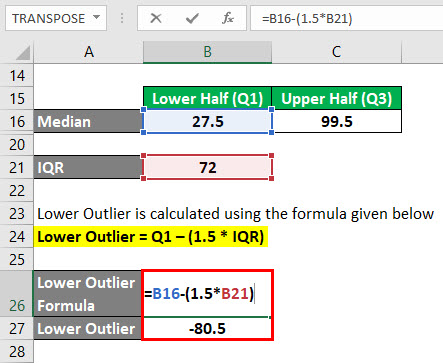
Lower Outlier is calculated using the formula given below
Lower Outlier = Q1 – (1.5 * IQR)
- Lower Outlier = 27.5 – (1.5 * 72)
- Lower Outlier = -80.5
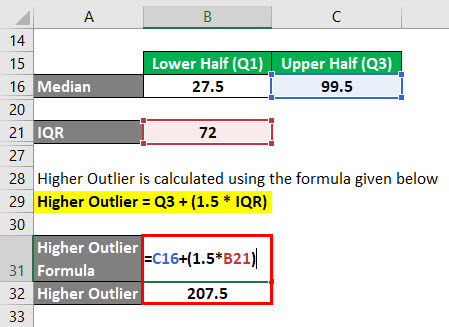
Higher Outlier is calculated using the formula given below
Higher Outlier = Q3 + (1.5 * IQR)
- Higher Outlier = 99.5 + (1.5 * 72)
- Higher Outlier = 207.5
Explanation
Step 1: Arrange all the values in the given data set in ascending order.
Step 2: Find the median value for the data that is sorted. Median can be found using the following formula. The following calculation simply gives you the position of the median value which resides in the date set.
Median = (n+1)/2
Where n is the total number of data available in the data set.
Step 3: Find the lower Quartile value Q1 from the data set. To find this, using the median value split the data set into two halves. From the lower half set of values, find the median for that lower set which is the Q1 value.
Step 4: Find the upper Quartile value Q3 from the data set. It is exactly like the above step. Instead of the lower half, we have to follow the same procedure the upper half set of values.
Step 5: Find the Interquartile Range IQR value. To find the Deduct Q1 value from Q3.
IQR = Q3-Q1
Step 6: Find the Inner Extreme value. An end that falls outside the lower side which can also be called as a minor outlier. Multiply the IQR value by 1.5 and deduct this value from Q1 gives you the Inner Lower extreme.
Lower Outlier =Q1 – (1.5 * IQR)
Step 7: Find the Outer Extreme value. An end that falls outside the higher side which can also be called a major outlier. Multiply the IQR value by 1.5 and sum this value with Q3 gives you the Outer Higher extreme.
Higher Outlier = Q3 + (1.5 * IQR)
Step 8: Values which falls outside these inner and outer extremes are the outlier values for the given data set.
Relevance and Uses of Outliers Formula
Outliers are very important in any data analytics problem. Outlier shows inconsistency in any data set as it is defined as the uncommon distant values in the data set from one to other. This is very useful in finding any flaws that occurred in the data set. Because when you place an error in the data set, it affects the mean and median hence may get big deviations in the result if Outliers are in the data set. Hence it is essential to find out Outliers from the data set in order to avoid serious problems in the statistical analysis.
Recommended Articles
This has been a guide to Outliers formula. Here we discuss how to calculate Outliers along with practical examples and downloadable Excel template. You may also look at the following articles to learn more –