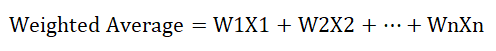Weighted Average Formula
The formula for calculating the Weighted Average is as follows:
Where,
- W denotes relative weight (in %)
- X denotes value
Examples of Weighted Average Formula
Let’s see a few examples to understand the Weighted Average Formula:
Example #1
Let’s assume Anand has invested the money in the following proportionate: 40% in investment A, 20% in investment B, and 40% in investment C. These investments have a rate of return as follows: Investment A is 15 %, Investment B is 10%, and Investment C is 20%, respectively. We need to calculate a weighted average for the rates of return Anand would receive.
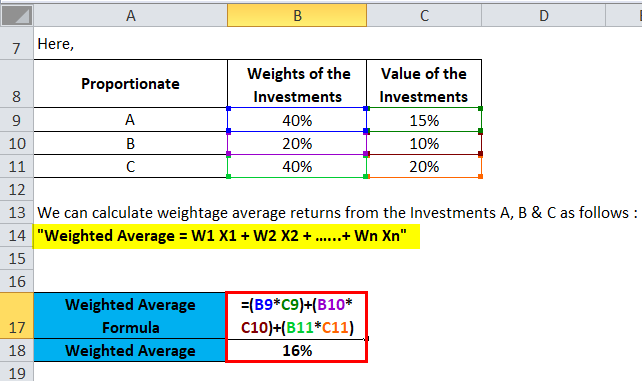
Here,
- We have Relative weights for investments A, B & C as 40%, 20%, and 40%, respectively.
- And, Value (Rate of Return) for investments A, B & C is 15%, 10%, and 20%, respectively.
By using the Weighted Average Formula, we get-
- Weighted Average = W1 X1 + W2 X2 + ……+ Wn Xn
- Weighted Average = 40%*15% + 20%*10% + 40%*20%
- Weighted Average = 16%
This shows Anand will be receiving 16% weightage average returns from Investments A, B & C.
Example #2
Let’s assume Anand has enrolled in a Maths course, and his final grade will be determined based on the following categories: tests 30%, final exam 40%, quizzes 15%, and homework 15%.
Anand has scored the following marks in each category: Tests-80, Final exam-65, quizzes-85, homework-90. Now we have to find out the overall grade of Anand.
Each category value must first be multiplied by its percentage to calculate a weighted average with percentages. Then all of these new values must be added together.
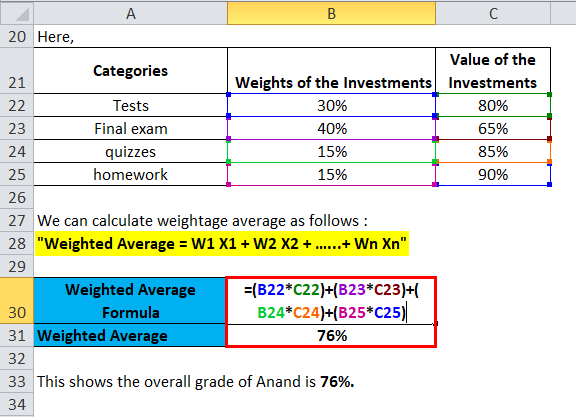
Here,
We have Relative weights for the following categories as follows:
- Tests 30%
- Final exam 40%
- quizzes 15%
- homework 15%
And, Value (Marks) for the categories as
- Tests-80
- Final exam-65,
- quizzes-85
- homework-90
By using the Weighted Average Formula, we get-
- Weighted Average = W1 X1 + W2 X2 + ……+ WnXn
- Weighted Average = (30%*80) + (40%*65) + (15%*85) + (15%*90)
- Weighted Average= 76.25 or 76%
This shows that the overall grade of Anand is 76%.
Example #3
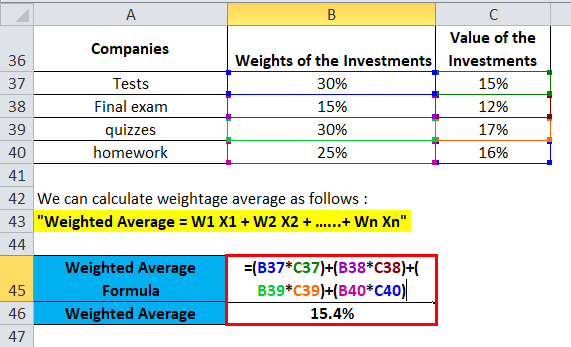
Let’s assume Jagriti has invested money in Stocks of different companies. Jagriti’s portfolio comprises 30% in Stock A, 15% in Stock B, 30% in Stock C, and the remaining 25% in Stock D. The expected return as per the current market situation on these Stocks are as follows: Return on Stock A is 15 %, Return on Stock B is 12 %, Return on Stock C is 17%, and Return on Stock D is 16 % respectively. Jagriti wants to calculate her average return on the portfolio as per the current market situation.
Here,
- We have Relative weights of the stocks in the portfolio as follows: A, B, C & D as 30%, 15%, 30%, and 25%, respectively.
- The value (Rate of Return) for the stocks is as follows: A, B, C & D as 15%, 12%, 17%, and 16%, respectively.
By using the Weighted Average Formula, we get-
- Weighted Average = W1 X1 + W2 X2 + W3 X3 + W4 X4 ……+ Wn Xn
- Weighted Average = (30%*15%) + (15%*12%) + (30%*17%) + (25%*16%)
- Weighted Average = 0.154 or 15.4%
This shows Jagriti will be receiving 15.4% weightage average returns from the Portfolio of stocks A, B, C, and D.
Explanation of Weighted Average Formula
The weighted average formula is used for calculating the average value for a particular set of numbers with different levels of relevancy. The weights must be represented in terms of total relevancy as a percentage. The weights taken should be equal to 100% or 1.
To Calculate the Weighted Average Formula, we need Relative Weightage and Value.
The first component is Relative Weightage, and the second is Value inputs. To calculate the Weighted Average, we must have a specific weightage for each variable taken as a value, and the weightage must equal 100%.
Significance and Use of Weighted Average Formula
The weighted average is used in various financial formulas. A few examples of Weighted average beta and weighted average cost of capital (WACC). We are familiar with finding the athematic mean or average for a series of items. We can simply add the values of all the items and divide them by the total number of items to calculate the average. This will only work if all the items are weighted equally. For example, for calculating the average monthly mobile bills for a year, we can simply add up the total billed amounts for the past twelve months and divide it by twelve; then, we can get a rough idea of the average bill paid since the mobile bill cycle is roughly for the same period of time i.e., One month.
Let’s say you want to calculate your Maths class’s current average course grade. Usually, most classes assign different weights to exams than homework assignments, internal tests, and competitions. In this case, you need to calculate a weighted average, which takes the specific weight of each topic, to calculate your course grade.
For example, in a few cases, use a weighted average instead of a simple one. The first case is when we want to calculate an average with different percentage values for different categories. The above example of the course grade is one of the similar cases. Secondly, when we have a large group of items with different regularities, if a company has a wide sales fluctuation due to the production of a seasonal product, it can use the weighted average formula. Suppose the company wants to calculate the average for their variable expenses. In that case, the company can use the weighted average formula and take the sales as the weight to understand their expenses better. And can compare the amount they produce or sell.
Weighted Average Calculator
You can use the following Weighted Average Calculator
| W1 | |
| X1 | |
| W2 | |
| X2 | |
| W3 | |
| X3 | |
| W4 | |
| X4 | |
| Weighted Average Formula | |
| Weighted Average Formula = | W1*X1 + W2*X2 + W3*X3 + W4*X4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Weighted Average Formula In Excel (With Excel Template)
Here, we will do the same example of the Weighted Average formula in Excel. It is very easy and simple. You need to provide the two inputs i.e. Relative weights and Rate of Return.
You can easily calculate the Weighted Average using the Formula in the template provided.
Weightage average returns from Investments A, B & C are calculated as:
The overall grade of Anand is calculated as:
Weight Age average returns from the Portfolio of stocks A, B, C, and D are calculated as:
You can download this Weighted Average Formula Excel Template here – Weighted Average Formula Excel Template
Recommended Articles
This has been a guide to a Weighted Average formula. Here, we discuss its uses along with practical examples. We also provide a Weighted Average Calculator with a downloadable Excel template. You may also look at the following articles to learn more –