Random Number Generator in R

Introduction to Random Number Generator in R

Random Number Generator in R is the mechanism which allows the user to generate random numbers for various applications such as representation of an event taking various values, or samples with random numbers, facilitated by functions such as runif() and set.seed() in R programming that enable the user to generate random numbers and control the generation process, so as to enable the user to leverage the random numbers thus generated in the context of real life problems.

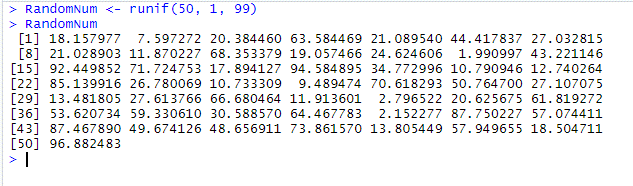
Here is one example below to generate and print 50 values between 1 and 99 using runif() function.

Code

RandomNum <- runif(50, 1, 99)
RandomNum

Output:

A random number generator helps to generate a sequence of digits that can be saved as a function to be used later in operations. Random number generator doesn’t actually produce random values as it requires an initial value called SEED. Random number generation can be controlled with SET.SEED() functions. SET.SEED() command uses an integer to start the random number of generations. Further, the generated random number sequence can be saved and used later.

For example, We will use the code to sample 10 numbers between 1 and 100 and repeat it a couple of times.

For the first time the SET.SEED() will start at seed as 5 and second time as seed as 12. Ten random numbers have been generated for each iteration.

Code:

set.seed(5) # random number will generate from 5
TenRandomNumbers <- sort(sample.int(100, 10))
TenRandomNumbers

Output:

Code:

set.seed(12) # random number will generate from 12
TenRandomNumbers <- sort(sample.int(100, 10))
TenRandomNumbers

Output:

Random Number Generator Functions

There are in-built functions in R to generate a set of random numbers from standard distributions like normal, uniform, binomial distributions, etc. In the next section we will see different functions like runif(), rnorm(), rbinom() and rexp() to generate random numbers.

1. Uniformly Distributed Random Numbers

To generate uniformly distributed random number runif() is used. Default range 0 – 1. First, we will require to specify the number required to be generated. In addition, the range of the distribution can be specified using the max and min argument.

Code

# To get 5 uniformly distributed Random Numbers
runif(5)

Output:

Code

# Get 5 random Numbers from 5 to 99
runif(5, min=5, max=99)

Output:

Code

#To generate 5 integers from 0 to 100
floor(runif(5, min=0, max=101))

Output:

Code

# Generating integers without replacement
sample(1:100, 5, replace=FALSE)

Output:

2. Normally Distributed Random Numbers

To generate numbers from a normal distribution rnorm() is used. Where mean is 0 and the standard deviation is 1. First, we will require to specify the number required to be generated. In addition, mean and SD (Standard deviation) can be specified arguments.

Code:

rnorm(5)

Output:

Code:

# using a different mean and standard deviation
rnorm(4, mean=70, sd=10)

Output:

Code:

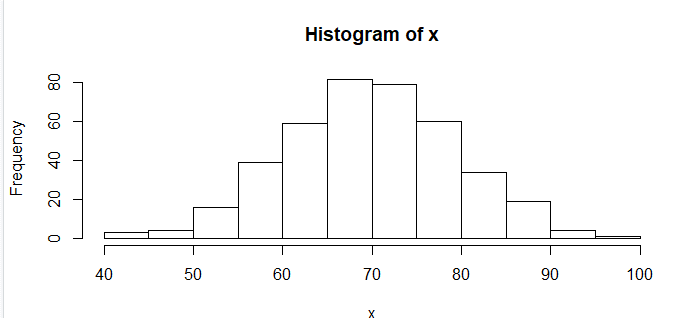
# histogram of the numbers to verify the distribution
X <- rnorm(400, mean=70, sd=10)
hist(X)

Output:

Using rnorm() for generating a normal distributed random number

3. Binomial Random Numbers

The binomial random numbers are a discrete set of random numbers. To derive binomial number value of n is changed to the desired number of trials. For instance trial 5, where n = 5

Code:

n= 5
p=.5
rbinom(1 ,n, p)
# 1 success in 5 trails
n= 5
p=.5
rbinom(19, n, p) # 10 binomial numbers

Output:

4. ExponEntially distributed random numbers

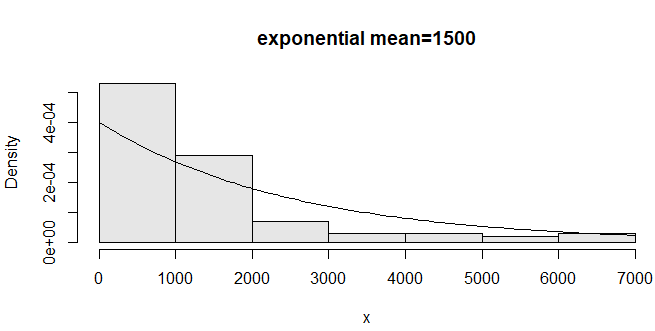
The exponential distribution is used to describe the lifetime of electrical components. For instance, the mean life of an electrical lamp is 1500 hours.

Code:

x=rexp(100, 1/1500)
hist(x, probability=TRUE, col= gray(.9), main="exponential mean=1500")
curve(dexp(x, 1/1500), add= T)

Output:

Generating Integer And Float Point Number

Now we will learn about generating random numbers for two types of numbers available in R. They are an integer and floating points or float point numbers. R will auto-detect the two categories and move across them as the need arises. An integer in R consists of the whole number that can be positive or negative whereas a floating-point number includes real numbers. It consists of a value that specifies the furthermost digit from the decimal point. The value is in binary and indication is available on the number of binary places to move over. To generate random integers built-in sample() function is reliable and quick. Business needs require you to analyze a sample of data. To select a sample R has sample() function. In order to generate random integers between 5 and 20 below the sample function code is used.

Code:

rn = sample(5:20, 5)
rn

Output:

Generating a random sample of 5

In the above example, five values have been generated as the argument stated. We have seen how a subset of random values can be selected in R. In real-time situation you will be required to generate a random sample from an existing data frame. Selecting a sample of data for observation from a large dataset is one of the jobs data engineers undertake in their day to day life.

Code:

Height_Weight_Data <- read.csv("test.csv") # to test this please download csv file
Height_Weight_Data
# Height_Weight_Data sample data frame; selecting a random subset in r
Sample <- Height_Weight_Data[sample(nrow(Height_Weight_Data), 5), ] # pick 5 random rows from dataset
Sample

Output:

Generating random sample from data frame names as Height_Weight_Data

Few things to remember regarding floating-point numbers.

• They are binary in nature.
• Limited in the real numbers represented.

Now let’s see how random floating number can be generated between -10 to 10

Code:

Random <- runif(n=10, min=-10, max=10)
Random

Output: 

Generating random float point numbers

Runif() refers to the random uniform. In the above example, we have derived 10 random distributed numbers between [-10:10]

Conclusion

In this article, we have discussed the random number generator in R and have seen how SET.SEED function is used to control the random number generation. We have seen how SEED can be used for reproducible random numbers that are being able to generate a sequence of random numbers and setting up a random number seed generator with SET.SEED(). The statistical method which requires generating random numbers is occasionally used during analysis. R is equipped with multiple functions such as uniform, Normal, Binomial, Poisson, Exponential and Gamma function which allows simulating the most common probability distribution.

Recommended Articles

This has been a guide to Random Number Generator in R. Here we discuss the introduction and functions of Random Number Generator in R along with the appropriate example. You can also go through our other suggested articles to learn more –

1. Linear Regression in R
2. Binomial Distribution in R
3. Logistic Regression in R
4. Line Graph in R