Updated March 18, 2023
Introduction to Line Drawing Algorithm
In this article, we will see an outline on the Line Drawing Algorithm. Line drawing on the computer means the computer screen is dividing into two parts rows and columns. Those rows and columns are also known as Pixels. In case we have to draw a line on the computer, first of all, we need to know which pixels should be on. A line is a part of a straight line that extends in the opposite direction indefinitely. The line is defined by two Endpoints. Its density should be separate from the length of the line.
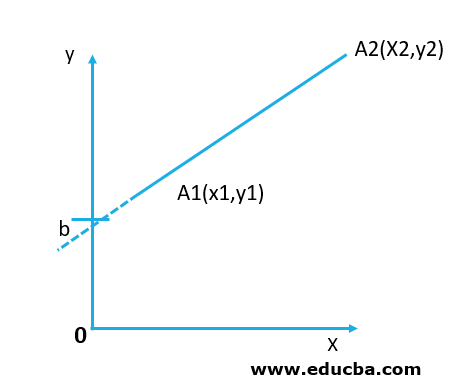
The formula for a line interception of the slope:
Y = mx + bIn this formula, m is a line of the slope and b is intercept of y in the line. In positions (x1, y1) and (x2, y2), two endpoints are specified for the line segment.
The value of slope m and b can be determined accordingly
• m = y2 – y1 / x2 – x1
• i.e. M = Δy / Δx
Example:
Line endpoints are (0,0) and (4,12). Plot the result to calculate each value of y as the x steps of 0 to 4.
Solution:
So we have a formula of equation of line:
Y = mx + b• m = y2 – y1 / x2 – x1 •m = 12 – 0 / 4 – 0 • m = 3 The y intercept b is then found by linking y1 and x1 to the y = 3 x + b formula, 0 = 3(0) + b. Therefore, b = 0, so the y = 3x line formula. The goal is to determine the next x, y location as quickly as possible by the previous one.
Types of Line Drawing Algorithm
Below given are the types of the algorithm:
1. Digital Differential Algorithm ( DDA)
An incremental conversion method is a DDA Algorithm and also we called Digital Differential Algorithm (DDA). This approach is characterized by the use of the results from the previous stage in each calculation.
Let us look at the examples given below:
Example #1
End point line are (x1 , y1) and (x2, y2)
- dx = x2 – x1
- dy = y2 – y1
so, now we will determine the length of the line if abs(dx) >= abs(dy) then length = abs (dx) else length = abs (dy)
- Δx = dx / length
- Δy = dy / length
- X = x1
- Y = y1
Setpixel (round (x), round (y));
- i = 1
while ( i <= length )
- x = x + Δx;
- y = y + Δy;
setpixel ( round (x) , round (y) );
i = i + 1
end while
Example #2
A line of end points (5, 4) & (6, 9) can be converted with the DDA.
Solution:
• dx = x2 – x1
• dx = 6 – 5 = 1
• dy = y2 – y1
• dy = 9 – 4
dy= 5
As, dx < dy then,
• length = y2 – y1 = 5
• dx = (x2 – x1) / length = 1/5 = 0.2
• dy = (y2- y1) / length = 5/5 = 1
x1 y1 x2 y2 L dx dy i x y
Result:
X1 |
Y1 |
X2 |
Y2 |
L |
Dx |
Dy |
I |
X |
Y |
Result |
3 |
2 |
4 |
7 |
5 |
.2 |
1 |
0 |
3.5 |
5.5 |
3.5, 5.5 |
1 |
3.9 |
1.5 |
3.9,1.5 |
|||||||
2 |
4.9 |
3.5 |
4.9,3.5 |
|||||||
3 |
5.1 |
7.5 |
5.1,7.5 |
|||||||
4 |
3.7 |
4.5 |
3.7,4.5 |
|||||||
5 |
4.5 |
7.5 |
4.5,7.5 |
Limitation of DDA Algorithm
- Arithmetic for floating and rounding points are time-consuming procedures.
- A round-off error may lead to a distance from the true long-line segment path by the measured pixel location.
2. The Bresenham Line Algorithm
The Scan conversion algorithm is Bresenham-algorithm. This algorithm offers the main advantage of using only integer calculations.
1. Endpoints of the row and store the left endpoint in (x1, y1)
2. For the decision parameter to get the first value Δx i.e. Dx, Δy i.e. Dy, 2 Δy and 2 Δx.
3. Initialize starting
4. Initialize i =1 as a counter,
Otherwise, the next point to plot is (xk + 1, yk + 1) and Repeat step 4 ( Δx – 1 ) times.
Adjustment
For m > 1, we can say if we increase x every time we increase y.
After the decision variable pk will be resolved the formula is very similar, only the x and y in the equation will be replaced.
Bresenham Line Algorithm Summary
These are the following advantages to the Bresenham line algorithm:
• A fast incremental algorithm.
• This uses only integer calculations.
DDA has the following problems when compared with the DDA algorithm:
• The pixelated line can be distant from the expected accumulation of round-off errors.
• Time is required for rounding operations and floating points arithmetic.
Recommended Articles
This has been a guide to Line Drawing Algorithm. Here we discuss what is line drawing algorithm along with the various examples. You may also have a look at the following articles to learn more–