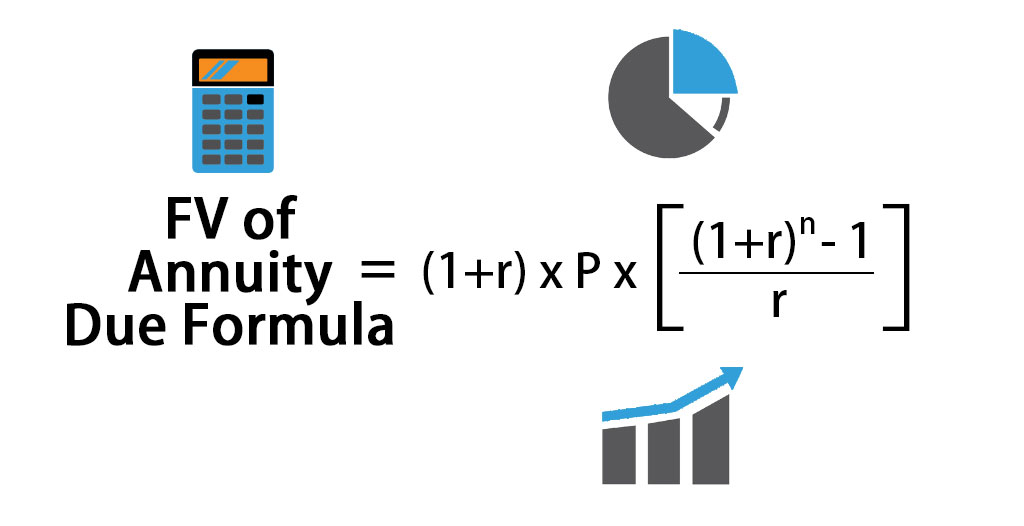Updated July 27, 2023
Future Value of Annuity Due Formula (Table of Contents)
- Future Value of Annuity Due Formula
- Examples of Future Value of Annuity Due Formula (With Excel Template)
- Future Value of Annuity Due Formula Calculator
Future Value of Annuity Due Formula
The formula for calculating Future Value of Annuity Due:
Where,
- P = Periodic Payment
- R = Rate per Period
- N = Number of Periods
Examples of Future Value of Annuity Due Formula (With Excel Template)
Let’s take an example to understand the calculation of Future Value of Annuity Due in a better manner.
Example #1
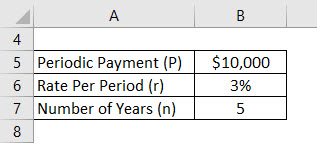
Let’s assume that an Anand have deposited $10,000 per year and the effective rate his account is offering is 3%. Now Anand wants to calculate his future balance after 5 years with assuming first deposit from today onwards.
Solution:
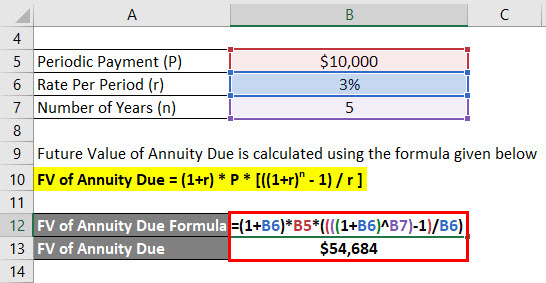
Future Value of Annuity Due is calculated using the formula given below
FV of Annuity Due = (1+r) * P * [((1+r)n – 1) / r ]
- FV of Annuity Due = (1+ 3%) * $10,000 * ((((1 + 3%)^5) – 1) / 3%)
- FV of Annuity Due = $54,684
Anand will be getting $54,684 future balance after 5 years.
Example #2
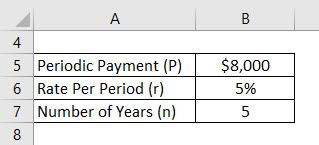
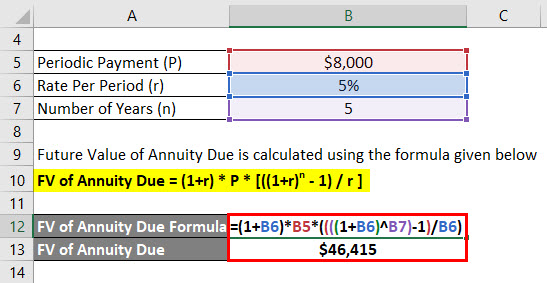
Let’s assume that a Jagriti has deposited $8,000 per year and the effective rate his account is offering is 5%. Now Jagriti wants to calculate his future balance after 5 years with assuming first deposit from today onwards.
Solution:
Future Value of Annuity Due is calculated using the formula given below
FV of Annuity Due = (1+r) * P * [((1+r)n – 1) / r ]
- FV of Annuity Due = (1+ 5%) * $8,000 * ((((1 + 5%)^5) – 1) / 5%)
- FV of Annuity Due = $46,415
Jagriti will be getting $46,415 future balance after 5 years.
Example #3
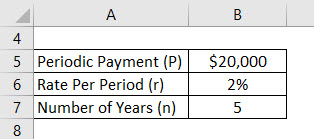
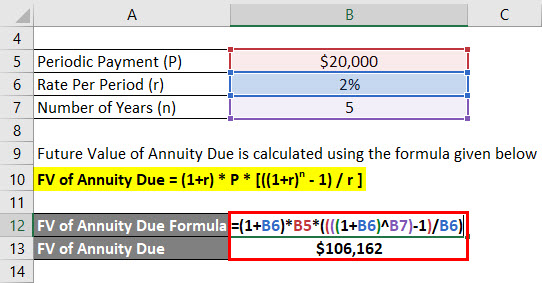
Let’s assume that an Anandriti has deposited $20,000 per year and the effective rate his account is offering is 2%. Now Anandriti wants to calculate his future balance after 5 years with assuming first deposit from today onwards.
Solution:
Future Value of Annuity Due is calculated using the formula given below
FV of Annuity Due = (1+r) * P * [((1+r)n – 1) / r ]
- FV of Annuity Due = (1+ 2%) * $20,000 * ((((1 + 2%)^5) – 1) / 2%)
- FV of Annuity Due = $1,06,162
Anandriti will be getting $1,06,162 future balance after 5 years.
Explanation
To calculate the ending value for a series of cash flows or payment where the first installment is received instantly, we use the Future Value of annuity due. The first instant installment or payment distinguish the annuity due to the ordinary annuity. An immediate or instant annuity is referred to as an annuity due.
It calculates the value of cash flows at a future period. The usage of the FV of annuity due is different in real situations than the present value of an annuity due. For example, suppose that a company or an individual buy an annuity and have paid the first installment today. We can use the example to explain further, suppose a company or an individual want to buy an annuity from anyone and have made the first payment today. In order to calculate the price to pay in this situation, we can use the present value of annuity due formula. However, if we want to calculate the remaining balance after saving interest for 5 years in the account and we decided to pay the first installment today, in this case, the future value of an annuity is used.
Annuity due can be explained as a type of annuity where cash flows occur at the starting of each period. Because of the advanced nature of cash flows, each cash flow is subject to the compounding effect for every additional period in case it is compared with an ordinary annuity. The future value of an ordinary annuity is lower than the future value of the annuity as the future value of annuity gets a periodic interest of the factor of one plus.
Relevance and Uses of Future Value of Annuity Due
Let’s understand the meaning of Future value and annuity due separately. Future value can be explained as the total value for a sum of cash which is to be paid in the future on a specific date. And an annuity due can be explained as the series of payments which is made at the beginning of each period in regular sequence. Therefore, future Value of annuity due can be explained as the total value on a specified date in future for a series of systematic/ periodic payment where the payments are made at the beginning of each period. This type of transaction and such a stream of payments can be seen for a pension plan beneficiary account.
The total value is the amount that the series of payments made in the future date will grow to, as a certain amount of interest is assumed, and earnings gradually increase over a certain period. The calculation of the future value of an ordinary annuity is identical to this but the only difference is that we add an extra period of payment which is being made at the beginning.
Future Value of Annuity Due Formula Calculator
You can use the following Future Value of Annuity Due Calculator
| P | |
| r | |
| n | |
| Future Value of Annuity Due Formula | |
| Future Value of Annuity Due Formula = | (1 +r) * P * [((1 +r)n- 1) / r] |
| = | (1 +0) * 0 * [((1 +0)0 -1) / 0] = 0 |
Recommended Articles
This has been a guide to the Future Value of Annuity Due Formula. Here we discuss how to calculate the Future Value of Annuity Due along with practical examples. We also provide the Future Value of Annuity Due calculator with a downloadable excel template. You may also look at the following articles to learn more –