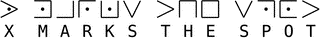Updated June 19, 2023
Algorithms and Cryptography
Algorithms and Cryptography are the First things; before I proceed and start boasting about myself and convert this blog into a boring side conversation, let’s first understand what Algorithms are and how they are related to Cryptography.
Algorithms
For those of you who think Algorithms are only connected to computer science, you are wrong. An algorithm is a method or a formula for solving a problem. And when I say problem, it can be any type of problem, whether Math, Science formulas, or even computer-based. Let me give you a simple
Example:
(A+b)2 = a2 +2ab + b2
Or it can be like:
Accrued Amount = Principal (1 + R.O.I*100*time)
Yes! Everything that is a formula can be an Algorithm. An algorithm is a set of rules for solving a problem, which, if done properly, will give a correct answer each time. Algorithms generally involve repeating a series of steps over and over, as in the borrowing and carrying algorithms and in the long multiplication and division algorithms. Algorithms include a variety of addition, subtraction, multiplication, and division.
But before you start thinking that I am taking some kind of Math lecture here, let me tell you that I am not. I am here to talk about Algorithms and Cryptography related to Computer Science. But before I proceed, let me give you some examples of simple algorithms to start with.
These examples are for pure noobs who have never done any kind of algorithmic stuff in their entire life. So, if you think you are smart enough, you can skip to the next section of Cryptography, where I will introduce some basics again before moving on to the next level.
So, here are a few examples of Addition Algorithms, which will get you started for now and give an idea of how algorithms are. Let’s start with basic Math:
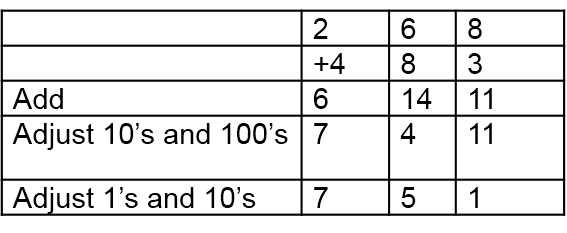
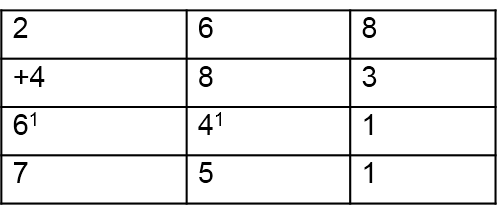
Left to Right Addition Algorithms
Starting at the left, add column-by-column, and adjust the result.
This process becomes so automatic for some people to start at the left and write the answer column by column, adjusting without writing any in-between steps. If asked to explain, they say something like this:
200 plus 400 is 600, but (looking at the next column) I need to adjust that, so write 7. Then, 60 and 80 are 140, but that needs adjusting, so write 5. Now, 8 and 3 are 11. No more to do. This technique easily develops from experiences with manipulatives, such as base-10 blocks and money and exchange or trading games. It is consistent with the left-to-right patterns learned for reading and writing.
Now some people may go all over nuts when reading about this. So, you may need to Google this stuff out to get an exact idea of what is happening over here.
Cryptography for Algorithms and Cryptography
Cryptography is the art of writing codes in a non-human readable manner. It is a method of storing and transmitting data in a particular form to can read and process it. You can say that Cryptography is a close cousin to the disciplines of cryptology and cryptanalysis.
Cryptography includes techniques such as microdots, merging words with images, and other ways to hide information in storage or transit. However, in today’s computer-centric world, cryptography is most often associated with scrambling plaintext (ordinary text, sometimes referred to as cleartext) into ciphertext (a process called encryption), then back again (known as decryption). Individuals who practice this field are cryptographers.
Encryption has been in use for many thousands of years. The following codes and ciphers encrypt and decrypt messages by hand:
Monoalphabetic Ciphers
Monoalphabetic Cipher uses the same substitution across the entire message. For example, knowing that the letter A is enciphered as the letter K will hold true for the entire message. These messages can be cracked using frequency analysis, educated guesses, or trial and error.
1. Ceaser Cipher
A Caesar cipher is one of the simplest (and easiest cracked) encryption methods. A Substitution Cypher involves replacing each letter of the secret message with a different letter of the alphabet, a fixed number of positions further in the alphabet.
Because each letter in the message directly translates to another letter, frequency analysis can be useful for deciphering the message. For example, E is the most common letter in English.
Thus, if the most common letter in a secret message is K, it is likely that K represents E. Common word endings such as ING, LY, and ES also give clues. A brute-force approach of trying all 25 possible combinations would also work to decipher the message.
In this example, each letter in the plaintext message has shifted to 3 letters in the alphabet.
- Plaintext: This is a secret message
- Ciphertext: wklv lv d vhfuhw phvvdjh
2. Atbash Cipher
The Atbash cipher is a case of a substitution cipher where the alphabet letters are reversed. In other words, all as are replaced with Zs, all Bs are replaced with Ys, and so on.
Because reversing the alphabet twice will get you the alphabet, you can encipher and decipher a message using the same algorithm.
Example:
- Plaintext: This is a secret message
- Ciphertext: Gsrh rh z hvxivg nvhhztv
The Keyword cipher is identical to the Caesar Cipher except that the substitution alphabet can be represented with a keyword.
You first write down the alphabet to create a substitution alphabet from a keyword. Below, you write down the keyword (omitting duplicate letters) followed by the alphabet’s remaining unused letters.
ABCDEFGHIJKLMNOPQRSTUVWXYZ
KEYWORDABCFGHIJLMNPQSTUVXZ
To encipher a plaintext message, you convert all letters from the top row to their corresponding letter on the bottom (A to K, B to E, etc.).
Frequency analysis and some educated guessing can easily crack these simple substitution ciphers.
3. Pigpen / Masonic Cipher
The pigpen cipher (sometimes called the Masonic Cipher or Freemason’s Cipher) is a simple substitution cipher exchanging letters for symbols based on a grid. The Freemasons developed and used the scheme in the early 1700s for record-keeping and correspondence. The example key shows how the letters can be assigned to the grid.
Polyalphabetic Ciphers
In a polyalphabetic cipher, the substitution may change throughout the message. In other words, the letter A may be encoded as the letter K for part of the message, but later on, it might be encoded as the letter W.
1. Vigenere Cipher
In a Caesar Cipher, each letter of the alphabet shifts along with some number of places; for example, in a Caesar cipher of shift 3, A would become D, B would become E, and so on. The Vigenere cipher uses several Caesar ciphers in sequence with different shift values.
A table of alphabets can encipher, termed tabula recta, Vigenere square, or Vigenere table. It consists of the alphabet written out 26 times in different rows. Each alphabet shifted cyclically to the left compared to the previous alphabet, corresponding to the 26 possible Caesar ciphers. At various points in the encryption process, the Cipher uses a different alphabet from one of the rows. The alphabet at each point depends on a repeating keyword.
For example, suppose that the plaintext is:
ATTACKATDAWN
The person sending the message chooses a keyword and repeats it until it matches the length of the plaintext, for example, the keyword “LEMON”:
LEMONLEMONLE
Each letter is encoded by finding the intersection in the grid between the plaintext letter and the keyword letter. For example, the first letter of the plaintext, A, is enciphered using the alphabet in row L, which is the first letter of the key. This is done by looking at the letter in row L and column A of the Vigenere square, namely L. Similarly, for the second letter of the plaintext, the second letter of the key is useful; the letter in row E and column T is X. The rest of the plaintext is enciphered similarly:
- Plaintext: ATTACKATDAWN
- Key: LEMONLEMONLE
- Ciphertext: LXFOPVEFRNHR
Finding the ciphertext letter’s position in a row of the table and then taking the column label in which it appears as the plaintext perform decryption. For example, in row L, the ciphertext L appears in column A, which is the first plaintext letter. Looking up X in row E of the table decrypts the second letter; it appears in column T as a plaintext letter.
A Gronsfeld cipher is identical to the Vigenere cipher except that only ten rows are useful, which allows the keyword to be a number instead of a word.
Steganography for Algorithms and Cryptography
Steganography is the science of hiding information from people who would snoop on you. The difference between this and encryption is that the would-be snoopers may not be able to tell there’s any hidden information in the first place.
For example, picture files typically have a lot of unused space. This space could be useful for sending hidden messages. If you do encryption research, you may see the term steganography used occasionally. However, it is not true encryption (though it can still be quite effective), so I only mention it here for completeness.
So, if you want to start practicing cryptology, the best way would be to start solving algorithms, Ciphertext, and Steganography. Even though Steganography may seem easy and not true encryption, it is still one of the most useful encryption when it comes to basics and when you need to code something quickly and in the best way possible.
Recommended Articles
Here are some articles that will help you to get more detail about Algorithms and Cryptography, so go through the link.