Updated March 28, 2023

Introduction to Uninformed Search
An Uninformed search is a group of wide range usage algorithms of the era. These algorithms are brute force operations, and they don’t have extra information about the search space; the only information they have is on how to traverse or visit the nodes in the tree. Thus uninformed search algorithms are also called blind search algorithms. The search algorithm produces the search tree without using any domain knowledge, which is the brute force in nature. They are different from informed search algorithms in a way that you check for a goal when a node is generated or expanded, and they don’t have any background information on how to approach the goal.
Types of Uninformed Search Algorithms
Below are the various types of Uninformed Search Algorithms:
1. Breadth-First Search Algorithms
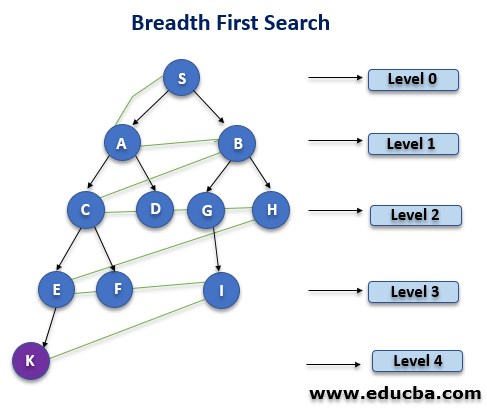
BFS is a search operation for finding the nodes in a tree. The algorithm works breadthwise and traverses to find the desired node in a tree. It starts searching operation from the root nodes and expands the successor nodes at that level before moving ahead and then moves along breadth wise for further expansion.
- It occupies a lot of memory space, and time to execute when the solution is at the bottom or end of the tree and uses the FIFO queue.
- Time Complexity of BFS is expressed as T (n) = 1+n2+n3+…….+ nd= O (nd) and;
- Space Complexity of BFS is O (nd).
- The breadth-first search algorithm is complete.
- The optimal solution is possible to obtain from BFS.
2. Depth First Search Algorithms
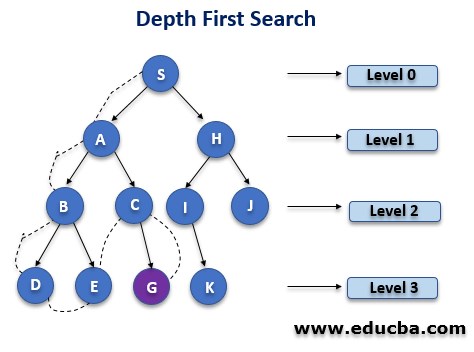
DFS is one of the recursive algorithms we know. It traverses the graph or a tree depth-wise. Thus it is known to be a depth-first search algorithm as it derives its name from the way it functions. The DFS uses the stack for its implementation. The process of search is similar to BFS. The only difference lies in the expansion of nodes which is depth-wise in this case.
- Unlike the BFS, the DFS requires very less space in the memory because of the way it stores the nodes stack only on the path it explores depth-wise.
- In comparison to BFS, the execution time is also less if the expansion of nodes is correct. If the path is not correct, then the recursion continues, and there is no guarantee that one may find the solution. This may result in an infinite loop formation.
- The DFS is complete only with finite state space.
- Time Complexity is expressed as T(n) = 1+ n2+ n3+………+ nm=O(nm).
- The Space Complexity is expressed as O (bm).
- The DFS search algorithm is not optimal, and it may generate large steps and possibly high cost to find the solution.
3. Depth Limited Search Algorithm
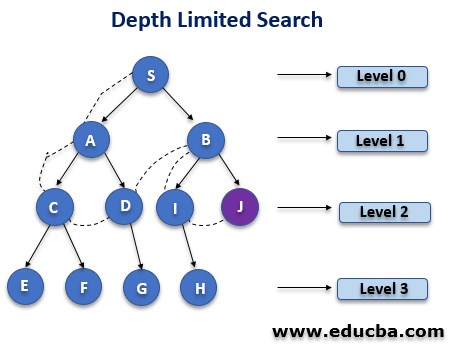
The DLS algorithm is one of the uninformed strategies. A depth limited search is close to DFS to some extent. It can find the solution to the demerit of DFS. The nodes at the depth may behave as if no successor exists at the depth. Depth-limited search can be halted in two cases:
-
- SFV: The Standard failure value which tells that there is no solution to the problem.
- CFV: The Cutoff failure value tells that there is no solution within the given depth.
- The DLS is efficient in memory space utilization.
- Time Complexity is expressed as O(bℓ).
- Space Complexity is expressed as O(b×ℓ).
- It has the demerit of incompleteness. It is complete only if the solution is above the depth limit.
4. Uniform-cost Search Algorithm
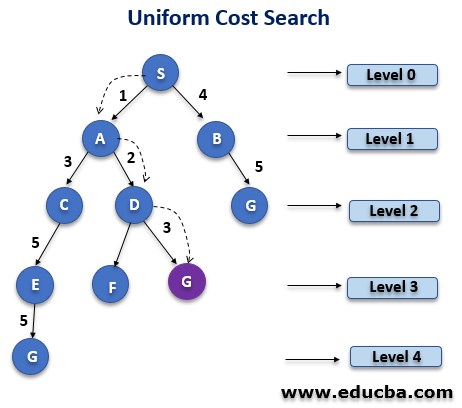
The UCS algorithm is used for visiting the weighted tree. The main goal of the uniform cost search is to fetch a goal node and find the true path, including the cumulative cost. The following are the properties of the UCS algorithm:
- The expansion takes place on the basis of cost from the root. The UCS is implemented using a priority queue.
- The UCS does not care for the number of steps, and so it may end up an infinite loop.
- The uniform-cost search algorithm is known to be complete.
- Time Complexity can be expressed as O(b1 + [C*/ε])/
- Space Complexity is expressed as O(b1 + [C*/ε]).
- We can say that UCs is the optimal algorithm as it chooses the path with the lowest cost only.
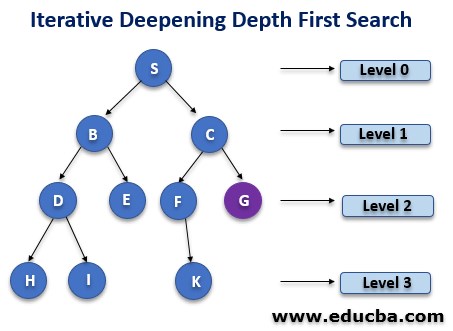
5. Iterative deepening depth-first Search
This algorithm is a combination of BFS and DFS searching techniques. It is iterative in nature. The best depth is found using it. The algorithm is set to search only at a certain depth. The depth keeps increasing at each recursive step until it finds the goal node.
- The power of BFS and DFS combination is observed in this algorithm.
- When the search space is large, it proves itself, and the depth is not known.
- This algorithm has one demerit, and it is that it iterates all the previous steps.
- The algorithm is known to be complete only if the branching factor is known r finite.
- Time Complexity is expressed as O(bd).
- Space Complexity is expressed as O(bd).
- This algorithm is optimal.
6. Bidirectional Search Algorithm
The Two way or Bidirectional search algorithm executes in a way that t has to run two searches simultaneously one in a forward direction and the other in the backward direction. The search will stop when the two simultaneous searches intersect each other to find the goal node. It is free to use any search algorithm discussed above, like BFS, DFS, etc.
- Bidirectional search is quick and occupies less memory.
- The implementation is difficult, and the goal node should be known in advance to execute it.
- The Bidirectional Search algorithm is found to be complete and optimal.
- Time Complexity is expressed as O(bd).
- Space Complexity is expressed as O(bd).

Conclusion
The Uninformed search strategies for searching is a multipurpose strategy that combines the power of unguided search and works in a brute force way. The algorithms of this strategy can be applied in a variety of problems in computer science as they don’t have the information related to state space and target problems.
Recommended Articles
This is a guide to Uninformed Search. Here we discuss the introduction and the Various types of Uninformed Search Algorithms like Breadth-First Search Algorithms, Depth Limited Search, etc. You can also go through our other suggested articles to learn more –


