Updated July 28, 2023
Introduction to Iterative Deepening Depth-First Search
Iterative deepening depth-first search (IDDFS) is an algorithm that is an important part of an Uninformed search strategy just like BFS and DFS. We can define IDDFS as an algorithm of an amalgam of BFS and DFS searching techniques. In IDDFS, We have found certain limitations in BFS and DFS so we have done hybridization of both the procedures for eliminating the demerits lying in them individually. We do a limited depth-first search up to a fixed “limited depth”. Then we keep on incrementing the depth limit by iterating the procedure unless we have found the goal node or have traversed the whole tree whichever is earlier.
Working Algorithm of IDDFS
In the uninformed searching strategy, the BFS and DFS have not been so ideal in searching the element in optimum time and space. The algorithms only guarantee that the path will be found in exponential time and space. So we found a method where we can use the amalgamation of space competence of DFS and optimum solution approach of BFS methods, and there we develop a new method called iterative deepening using the two of them. The main idea here lies in utilizing the re-computation of entities of the boundary instead of stocking them up. Every re-computation is made up of DFS and thus it uses less space. Now let us also consider using BFS in iterative deepening search.
- Consider making a breadth-first search into an iterative deepening search.
- We can do this by having aside a DFS which will search up to a limit. It first does searching to a pre-defined limit depth to depth and then generates a route length1.
- This is done by creating routes of length 1 in the DFS way. Next, it makes way for routes of depth limit 2, 3 and onwards.
- It even can delete all the preceding calculation all-time at the beginning of the loop and iterate. Hence at some depth eventually the solution will be found if there is any in the tree because the enumeration takes place in order.
Pseudo-code for IDDFS
1 IDDFS(T):
2 for d = 0 to infinity:
3 if (DLS(T, d)):
4 return 1
5 else
6 return 0
In order to implement the iterative deepening search we have to mark differences among:
- Breakdown as the depth limit bound was attained.
- A breakdown where depth bound was not attained.
While in the case once we try the search method multiple times by increasing the depth limit each time and in the second case even if we keep on searching multiple times since no solution exists then it means simply the waste of time. Thus we come to the conclusion that in the first case failure is found to be failing unnaturally, and in the second case, the failure is failing naturally.
Now let us focus on the Procedure of the IDDFS.
Example of Iterative Deepening Depth-First Search
Let us take an example to understand this
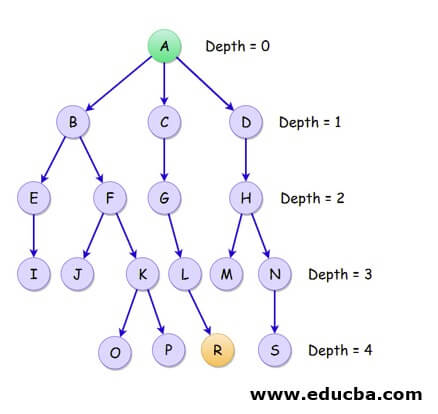
Here in the given tree, the starting node is A and the depth initialized to 0. The goal node is R where we have to find the depth and the path to reach it. The depth from the figure is 4. In this example, we consider the tree as a finite tree, while we can consider the same procedure for the infinite tree as well. We knew that in the algorithm of IDDFS we first do DFS till a specified depth and then increase the depth at each loop. This special step forms the part of DLS or Depth Limited Search. Thus the following traversal shows the IDDFS search.
This gives us a glimpse of the IDDFS search pattern.
Advantages and Disadvantages of IDDFS
Below are the advantages and disadvantages are given below:
Advantages
- IDDFS gives us the hope to find the solution if it exists in the tree.
- When the solutions are found at the lower depths say n, then the algorithm proves to be efficient and in time.
- The great advantage of IDDFS is found in-game tree searching where the IDDFS search operation tries to improve the depth definition, heuristics, and scores of searching nodes so as to enable efficiency in the search algorithm.
- Another major advantage of the IDDFS algorithm is its quick responsiveness. The early results indications are a plus point in this algorithm. This followed up with multiple refinements after the individual iteration is completed.
- Though the work is done here is more yet the performance of IDDFS is better than single BFS and DFS operating exclusively.
- Space and time complexities are expressed as: O(d) and here d is defined as goal depth.
- Let us consider the run time of IDDFS. Let say b>l where b is branching factor and l is the depth limit. Then next we search the goal node under the bound k. On the depth k, we say there may be bknodes that are only generated once. Similarly, the nodes at the depth limit k-1 is twice and thrice for k-2 depth. Thus the node generated at depth l is k times.
Disadvantages
- The time taken is exponential to reach the goal node.
- The main problem with IDDFS is the time and wasted calculations that take place at each depth.
- The situation is not as bad as we may think of especially when the branching factor is found to be high.
- The IDDFS might fail when the BFS fails. When we are to find multiple answers from the IDDFS, it gives back the success nodes and its path once even if it needs to be found again after multiple iterations. To stop the depth bound is not increased further.
Conclusion
Iterative deepening depth-first search is a hybrid algorithm emerging out of BFS and DFS. IDDFS might not be used directly in many applications of Computer Science, yet the strategy is used in searching data of infinite space by incrementing the depth limit by progressing iteratively. This is quite useful and has applications in AI and the emerging data sciences industry.
Recommended Articles
This is a guide to Iterative Deepening Depth-First Search. Here we discuss the example of Iterative Deepening Depth-First Search. You may also have a look at the following articles to learn more –