Introduction to Depth Limited Search
Depth limited search is the new search algorithm for uninformed search. The unbounded tree problem happens to appear in the depth-first search algorithm, and it can be fixed by imposing a boundary or a limit to the depth of the search domain. We will say that this limit as the depth limit, making the DFS search strategy more refined and organized into a finite loop. We denote this limit by l, and thus this provides the solution to the infinite path problem that originated earlier in the DFS algorithm. Thus, Depth limited search can be called an extended and refined version of the DFS algorithm. In a nutshell, we can say that to avoid the infinite loop status while executing the codes, and depth limited search algorithm is being executed into a finite set of depth called depth limit.
Algorithm
This algorithm essentially follows a similar set of steps as in the DFS algorithm.
- The start node or node 1 is added to the beginning of the stack.
- Then it is marked as visited, and if node 1 is not the goal node in the search, then we push second node 2 on top of the stack.
- Next, we mark it as visited and check if node 2 is the goal node or not.
- If node 2 is not found to be the goal node, then we push node 4 on top of the stack.
- Now we search in the same depth limit and move along depth-wise to check for the goal nodes.
- If Node 4 is also not found to be the goal node and depth limit is found to be reached, then we retrace back to nearest nodes that remain unvisited or unexplored.
- Then we push them into the stack and mark them visited.
- We continue to perform these steps in iterative ways unless the goal node is reached or until all nodes within depth limit have been explored for the goal.
When we compare the above steps with DFS, we may found that DLS can also be implemented using the queue data structure. In addition to each level of the node needs to be computed to check the finiteness and reach of the goal node from the source node.
Depth-limited search is found to terminate under these two clauses:
- When the goal node is found to exist.
- When there is no solution within the given depth limit domain.
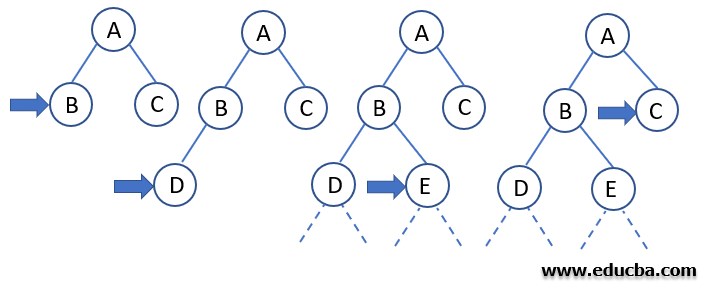
Example of DLS Process
If we fix the depth limit to 2, DLS can be carried out similarly to the DFS until the goal node is found to exist in the tree’s search domain.
Algorithm of the example
- We start with finding and fixing a start node.
- Then we search along with the depth using the DFS algorithm.
- Then we keep checking if the current node is the goal node or not.
If the answer is no: then we do nothing.
If the answer is yes: then we return.
- Now we will check whether the current node is lying under the depth limit specified earlier or not.
If the answer is not: then we do nothing.
If the answer is yes, we will explore the node further and save all of its successors into a stack.
- Now we call the function of DLS iteratively or recursively for all the nodes of the stack and go back to step 2.
Thus we have successfully explored all the nodes in the given depth limit and found the goal node if it exists within a specified depth limit.
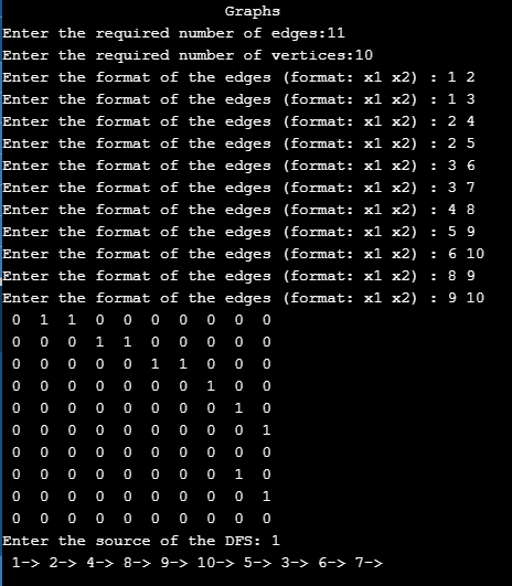
C program
Code:
#include <stdio.h>
#include <stdlib.h>
/*ADJACENCY MATRIX*/
int source,X,Y,time,visited[20],Z[20][20];
void DFS(int p)
{
int q;
visited[p]=1;
printf(" %d->",p+1);
for(q=0;q<X;q++)
{
if(Z[p][q]==1&&visited[q]==0)
DFS(q);
}
}
int main()
{
int p,q,x1,x2;
printf("\t\t\tGraphs\n");
printf("Enter the required number of edges:");
scanf("%d",&Y);
printf("Enter the required number of vertices:");
scanf("%d",&X);
for(p=0;p<X;p++)
{
for(q=0;q<X;q++)
Z[p][q]=0;
}
/*creating edges : */
for(p=0;p<Y;p++)
{
printf("Enter the format of the edges (format: x1 x2) : ");
scanf("%d%d",&x1,&x2);
Z[x1-1][x2-1]=1;
}
for(p=0;p<X;p++)
{
for(q=0;q<X;q++)
printf(" %d ",Z[p][q]);
printf("\n");
}
printf("Enter the source of the DFS: ");
scanf("%d",&source);
DFS(source-1);
return 0;
}
Output:
Advantages and Disadvantages of Depth Limited Search
Below are the advantages and disadvantages are below:
Advantages of Depth Limited Search
- Depth limited search is better than DFS and requires less time and memory space.
- DFS assures that the solution will be found if it exists infinite time.
- There are applications of DLS in graph theory particularly similar to the DFS.
- To combat the disadvantages of DFS, we add a limit to the depth, and our search strategy performs recursively down the search tree.
Disadvantages of Depth Limited Search
- The depth limit is compulsory for this algorithm to execute.
- The goal node may not exist in the depth limit set earlier, which will push the user to iterate further adding execution time.
- The goal node will not be found if it does not exist in the desired limit.
Performance Measures
- Completeness: The DLS is a complete algorithm in general except the case when the goal node is the shallowest node, and it is beyond the depth limit, i.e. l < d, and in this case, we never reach the goal node.
- Optimality: The DLS is a non-optimal algorithm since the depth that is chosen can be greater than d (l>d). Thus DLS is not optimal if l > d
- Time complexity is expressed as: It is similar to the DFS, i.e. O(bl), where 1 is the set depth limit.
- Space Complexity is expressed as: It is similar to DFSe. O(bl), where 1 is specified depth limit.
Conclusion – Depth Limited Search
DLS algorithm is used when we know the search domain, and there exists a prior knowledge of the problem and its domain while this is not the case for uninformed search strategy. Typically, we have little idea of the goal node’s depth unless one has tried to solve it before and has found the solution.
Recommended Articles
This is a guide to Depth Limited Search. Here we discuss Depth Limited Search Process’s example and the algorithms, advantages, and disadvantages. You may also have a look at the following articles to learn more –