Updated July 24, 2023
Standard Error Formula (Table of Contents)
What is Standard Error Formula?
In statistics, the term “standard error” of a statistic refers to the estimate of the standard deviation of the sample mean from the true population mean.
To put it simply, just as standard deviation measures each individual’s dispersion value from the sample mean, the standard error of mean measures the dispersion of all the sample means around the population mean.
Derive the formula for standard error by dividing the sample standard deviation by the square root of the sample size. Although population standard deviation should be used in the computation, it is seldom available. In this context, we use the sample standard deviation as a proxy for the population standard deviation. We represent it mathematically as,
Where,
- s: √Σni(xi-x̄)2 / n-1
- xi: ith Random Variable
- x̄: Sample Mean
- n: Sample Size
Examples of Standard Error Formula (With Excel Template)
Let’s take an example to understand the calculation of Coupon Bond in a better manner.
Standard Error Formula – Example #1
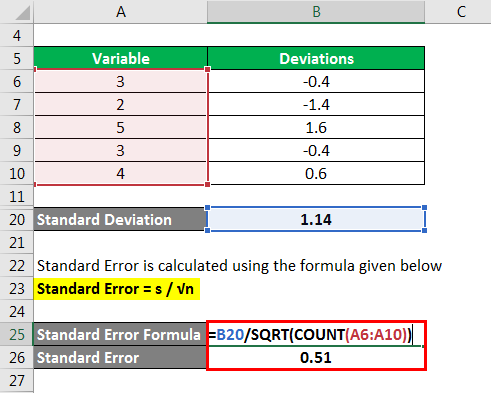
Take the example of a survey where 100 respondents were asked to provide feedback on the recently concluded college fest. They were asked to rate the fest on a scale of 1 to 5, with 5 being the best. Now, a random sampling method was used to build a sample of 5 responses out of the 100 responses. The selected responses are – 3, 2, 5, 3, and 4. Calculate the standard error of the statistic based on the selected responses.
Solution:
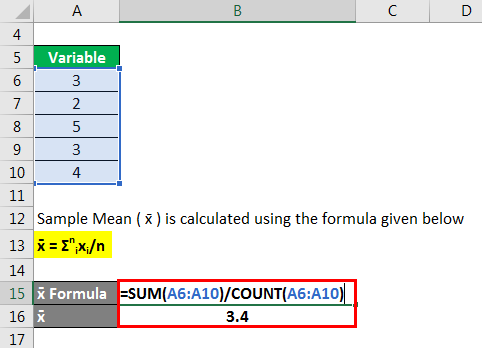
Sample Mean ( x̄ ) is calculated using the formula given below
x̄ = Σnixi/n
- Sample Mean ( x̄ ) = (3 + 2 + 5 + 3 + 4) / 5
- Sample Mean ( x̄ ) = 3.4
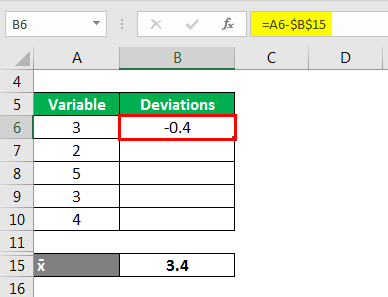
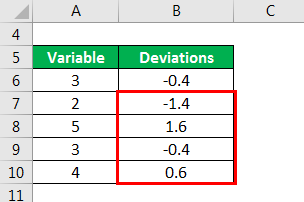
Calculated Deviation as
Similarly Calculated below
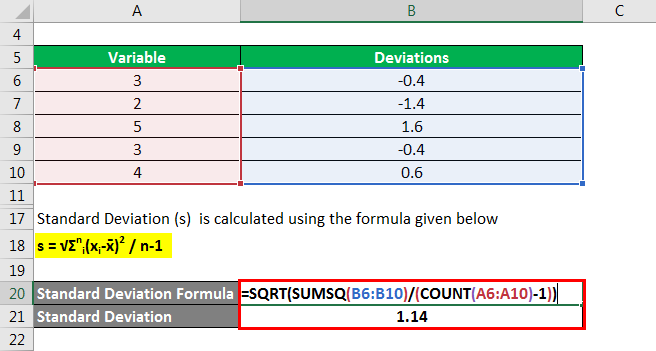
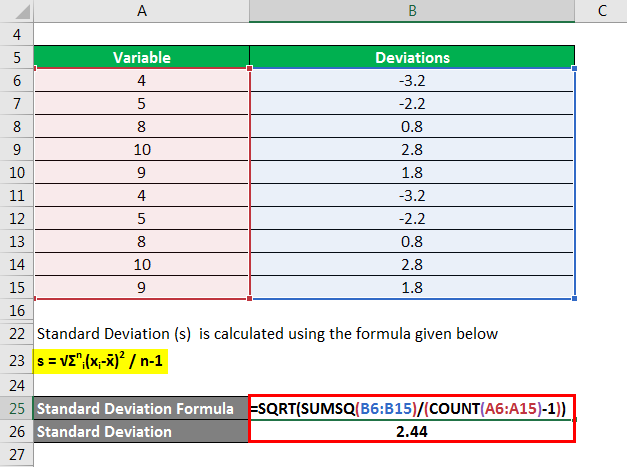
Calculate the standard deviation (s) using the formula below
s = √Σni(xi-x̄)2 / n-1
- Standard Deviation = √ [{(3 – 3.4)2 + (2 – 3.4)2 + (5 – 3.4)2 + (3 – 3.4)2 + (4 – 3.4)2} / (5 – 1)]
- Standard Deviation = 1.14
The standard error is calculated using the formula given below
Standard Error = s / √n
- Standard error = 1.14 / √5
- Standard Error = 0.51
Therefore, the standard error of the sample mean is 0.51.
Standard Error Formula – Example #2
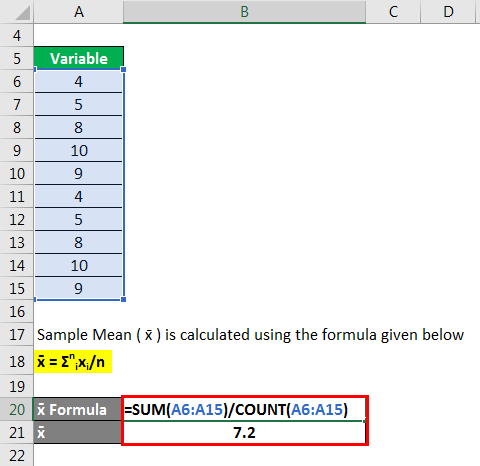
Let us take the example of a survey conducted at an office in New York where around 1,000 employees were asked how much they liked the work that they were doing in their current profile. They were to rate on a scale of 1 to 10, with 10 being the best. Then a sample of 10 responses was selected, and the responses were – 4, 5, 8, 10, 9, 5, 9, 8, 9, and 7. Calculate the standard error of the statistic based on the selected responses.
Solution:
Sample Mean ( x̄ ) is calculated using the formula given below
x̄ = Σnixi/n
- Sample Mean ( x̄ ) = (4 + 5 + 8 + 10 + 9 + 5 + 9 + 8 + 9 + 7) / 10
- Sample Mean ( x̄ )= 7.2
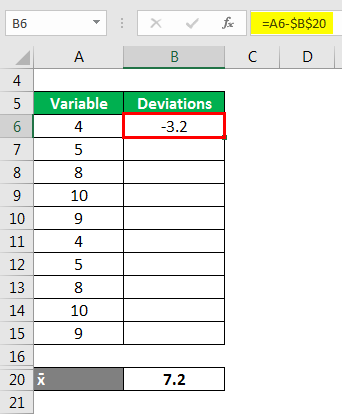
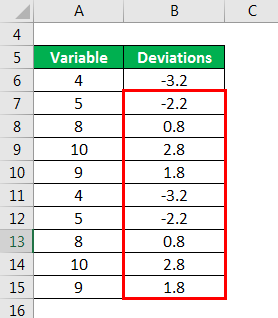
Calculated Deviation as
Similarly Calculated below
Use the formula below to calculate the standard deviation (s)
s = √Σni(xi-x̄)2 / n-1
- Standard Deviation = √ [{(4 – 7.2)2 + (5 – 7.2)2 + (8 – 7.2)2 + (10 – 7.2)2 + (9 – 7.2)2 + (5 – 7.2)2 + (9 – 7.2)2 + (8 – 7.2)2 + (9 – 7.2)2 + (7 – 7.2)2} / (10 – 1)]
- Standard Deviation = 2.44
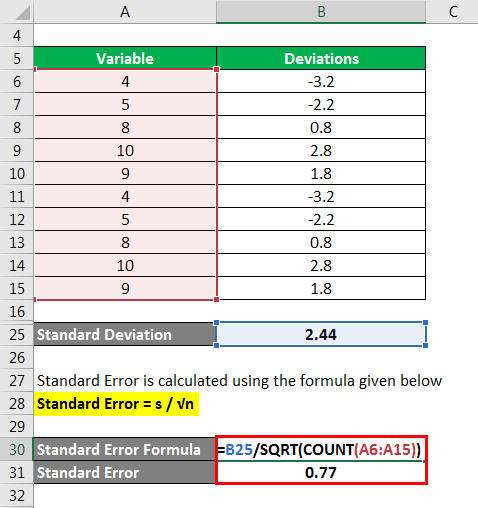
Calculate the standard error using the formula below:
Standard Error = s / √n
- Standard error = 2.44 / √10
- Standard Error = 0.77
Therefore, the standard error of the sample mean is 0.77.
Explanation
Derive the formula for standard error by following the steps below:
Step 1: First, collect the sample variables from the population based on a certain sampling method. We denote the sample variables by x, where xi refers to the ith variable of the sample.
Step 2: Next, determine the sample size, which is the total number of variables in the sample. It is denoted by n.
Step 3: Next, derive the sample mean by dividing the summation of all the variables in the sample (step 1) by the sample size (step 2). Denote this by, and represent it mathematically as
x̄ = Σnixi/n
Step 4: Next, compute the sample standard deviation (s), which involves a complex calculation that uses each sample variable (step 1), sample mean (step 3), and sample size (step 2), as shown below.
s = √Σni(xi-x̄)2 / n-1
Step 5: Finally, derive the formula for standard error by dividing the sample standard deviation (step 4) by the square root of the sample size (step 2), as shown below.
Standard Error = s / √n
Relevance and Use of Standard Error Formula
It is essential to understand the concept of standard error as statisticians predominantly use it as it allows them to measure the precision of their sampling method. Statisticians usually use the sample from a large pool of data as it is difficult to process such a huge data set, and as such, sampling makes the task a lot easier. So, standard error helps estimate how far the sample mean is from the true population means.
In the case of finite population standard deviation, an increase in sample size will eventually reduce the standard error of the sample mean to zero as the population’s estimation will improve. The sample standard deviation will also become approximately equal to the population standard deviation with the increase in sample size.
In the normally distributed sampling distribution, the sample mean, quantiles of the normal distribution, and standard error can be used in the calculation of the population mean’s confidence intervals.**
Standard Error Formula Calculator
You can use the following Standard Error Formula Calculator
| s | |
| √n | |
| Standard Error Formula
| |
| Standard Error Formula | = |
|
|
Recommended Articles
This is a guide to Standard Error Formula. Here we discuss how to calculate Standard Error, practical examples, and a downloadable Excel template. You may also look at the following articles to learn more –