Updated July 24, 2023
Forward Rate Formula (Table of Contents)
What is the Forward Rate Formula?
Forward Interest Rate is the interest rate that is decided initially at today’s price for a certain future period. It is the only rate decided based on mutual concern and agreed upon to borrow or lend a sum of money at some future date. Forward rates can also be derived from spot interest rates, the yields we obtain on zero-coupon bonds through bootstrapping.
A forward rate arises due to the forward contract. Even though the commitment between two parties leads to the successful execution of a forward contract, it has been split into two legs; the first commitment is to deliver, sell, or take a short position on the asset, and on another leg, to take delivery, buy, or take a long position on the asset.
It states that it produces a rate so that two consecutive one-year maturities offer the same return as two-year maturity offers. It is the interest rate an investor has guaranteed to get the same returns between the first investment maturity and second maturity while picking between the shorter or longer term.it is represented mathematically as below:
where,
- st:t-period Spot Rate
- st-1:t-1-period Spot Rate
- ft-1, 1: forward Rate applicable for the period (t-1,1)
Examples of Forward Rate Formula (With Excel Template)
Let’s take an example to understand the calculation of the Forward Rate in a better manner.
Forward Rate Formula – Example #1
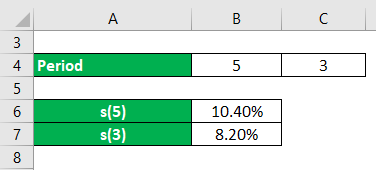
Suppose an investor tries to determine what yield he will obtain on a two-year investment made three years from now. While the spot rate of interest for three years is 8.2% p.a, and the spot yield for five years is 10.4% p.a; on zero-coupon bonds.
Solution:
Forward Rate is calculated using the formula given below
Forward Rate f(t-1, 1) = [(1 + s(t))t / (1 + s(t-1)t-1 ] – 1
- (1+f(3,2))^2 = (1+s(5))^5 / (1+s(3))^3
- f(3,2) =[{(1+s(5))^5/(1+s(3))^3)^(1/2)}] -1
- f(3,2) = 0.1378 = 13.78%p.a
It shows 2-year yields after 3 years from now would be 13.784%p.a
Forward Rate Formula – Example #2
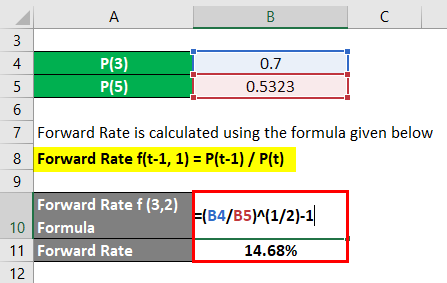
If we take the same as discussed above, the three-year zero-coupon bond price is $0.70 per unit nominal, and the five-year bond cost is $0.5323 per unit nominal.
Solution:
From the Forward rate equation, we can assume (1+s(t))^t = P(t)^-1 and (1+s(t-1))^(t-1) = P(t-1)^-1, where P(t-1) is a unit zero-coupon price with term(t-1) and P(t)is the unit zero-coupon price bond with term t year. So we can write an equation in such a way of these prices as follows:
Forward Rate calculates by using the formula given below
Forward Rate f(t-1, 1) = [(1 + s(t))t / (1 + s(t-1)t-1 ] – 1 = P(t-1) / P(t)
- (1+f(t,1))^1 = [(1 + s(t))t / (1 + s(t-1)t-1 ]
- (1+f(3,2))^2 = P(3) / P(5)
- f (3,2) =[P(3) / P(5)^(1/2)}] -1
- f(3,2) = [(0.07 / 0.5323 )^(1/2)}] -1
- f(3,2) = 0.14676 = 14.68%p.a
Explanation
Let’s elaborate on this concept with the help of an example; an oil trader is expecting a delivery of oil barrels in four months. Due to price fluctuation, its price keep on varying. So the trader has decided to enter into a forward contract to buy oil from the seller. Both parties enter into a contract through this contract and agree to fix an interest rate in advance at a certain time ‘t’.
How to Calculate Forward Interest Rates?
To determine the forward rates, we must satisfy the no-arbitrage condition, where no two investors should earn the arbitrage between interest periods. Suppose an investor is interested in investing his funds for two years. He has two choices:
- Invest directly in a 2-year bond or,
- Invest for a 1-year bond and then at the end of the year again invest for the next year in a one-year bond.
Step1. Determine the spot rate s1 of the on-year, s2 spot rate of the two years and one-year forward rate 1f1 for one year from now.
Step2. If the initial value of an investment for the 2-year bond is $1, then the final outcome after 2 years would be =(1+s2)^2
Step3: To avoid the arbitrage between the two methods of investment, the value of an investment in the second choice for 2 years would be = (1+s1)(1+1f1)
(1+s2)2 = (1+s1) (1+1f1)
Step 4: When we have two spot rates, we can rearrange the above equation and can obtain the one-year forward rate for one year from now.
1f1 = (1+s2)^2/(1+s1) – 1
The standard representation of the formula in a mathematical term as such:
Forward Rate ft-1, 1=(1+st)t ÷ (1+st-1)t-1 -1
where,
- st:t-period Spot Rate
- st-1:t-1-period Spot Rate
- ft-1, 1: forward Rate applicable for the period (t-1,1)
Relevance and Use of Forward Rate Formula
Normally, the forward rates are used by the investors, who believe that they understand market trends from the immediate past to the current market scenario relative to prices of specific item changes concerning time. Merely, it is the belief of the potential investors that the real future rates will always be higher or lower than the present stated market rate. It could be a signal for potential investors and crack the opportunity.
Suppose we try to identify the situation based on an economic indicator. In that case, we can analyze the spot rate and the forward rate changes concerning time, where buyers and sellers use a spot rate, who believe in immediate buy and sale and act as a starting point to any financial transaction. At the same time, a forward rate is merely a market’s expectation for future prices. It is an economic indicator of the market’s expected performance.
To make the best decision- it is more likely to return the highest possible yield on investment. It draws a positive impact on the forward rate. Above that, it is merely an estimate of where interest rates are more likely to be in the next six months from the time of the investor’s initial investment.
Recommended Articles
This is a guide to Forward Rate Formula. Here we discuss how to calculate Forward Rate along with practical examples. We also provide a downloadable Excel template. You may also look at the following articles to learn more –