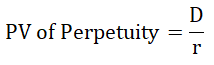Perpetuity Formula (Table of Contents)
Perpetuity Formula
Perpetuity can be termed as a type of annuity which gets an innumerable amount of periodic payment. On the other hand, an annuity typically means a consistent payment against a financial instrument. The primary objective of a perpetuity formula is to fellow the present and future cash flow.
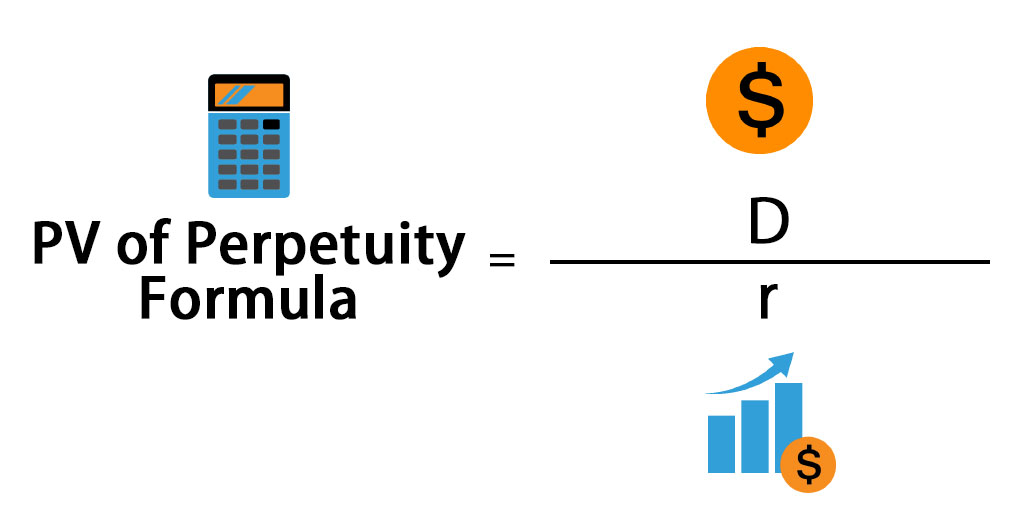
Here’s the Perpetuity formula –
Where,
- PV= present value
- D = dividend or coupon for a period
- r = discount rate
The most common examples of perpetuity formula are when preferred stocks are issued in the UK and in most of the circumstances they received the dividends prior 2 the equity shareholders dividend and the rate of dividend is fixed. Thus the value of preferred stocks can be can be calculated by using the perpetuity formula for an innumerable time frame.
There is another instance when the perpetuity can be changed depending on the same payment but a change in the dividend rate. If the rate of discount is lowered, the denominator also becomes lower and the value will tend to increase.
Example of Perpetuity Formula
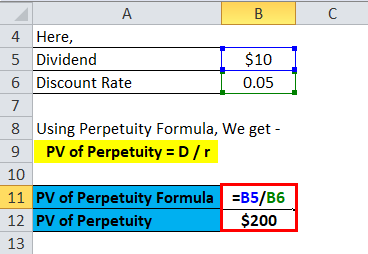
A person has purchased a bond with a coupon payment of $10 per year and it continues for an infinite time frame. Assuming a coupon discount rate of 5%.
Using Perpetuity Formula, We get –
- PV of Perpetuity = D / r
- PV of Perpetuity = $10 / 0.05
- PV of Perpetuity = $200
Therefore the amount which he expected to pay for this perpetuity would be $200
It should be noted that in the above formula the time frame is fixed.
4.9 (3,296 ratings)
View Course
How the present growing formula is derived?
A perpetuity series which is growing in terms of periodic payment and is considered to be indefinite which is growing at a proportionate rate.
Therefore the formula can be summed up as follows:
PV = D/ (1+r) + D (1+g) / (1+r) ^2 + D (1+g) ^2 ….
The perpetuity series is considered to continue for an infinite period. The formula can be again written and presented as the following example:
John has invested into a bond which pays him coupon payment for an infinite period of time. This bond pays John $200 every year. If we assume that the discount rate is 6%, how much John should pay for this bond?
- Dividend = 200
- Discount Rate = 0.06
Using Perpetuity Formula, We get –
- PV of Perpetuity = D / r
- PV of Perpetuity = 200 / 0.06
- PV of Perpetuity = $3333.33
Therefore the coupon rate is $333.33 which has been paid by John during a purchase of the Bond.
Features of Perpetuity Formula
- Perpetuity is called the annuity which is infinite and does not have an end.
- It is related to the cash payment which continues forever.
- A particular date should be mentioned from which the perpetuity starts and tends to continue for infinite future.
PV= A/r
Where,
PV represents the present value of a perpetuity
A represents the amount of periodic payment
Besides, the present value of perpetuity can also be determined by the following steps:
Step 1 To find the annual payment, a rate of interest and growth rate of perpetuity
Step 2 Put the actual number into the formula
* Present value of f\growth perpetuity = P / (i-g)
Where P represents annual payment, ‘i’ the discount rate
and ‘g’ is the growth rate.
Explanation of Perpetuity Formula
It is considered that the perpetuity formula detects the free cash flow in the terminal year of operation. It is expected that a company or more specifically a going concern will likely to do its operation forever. Thus it is assumed from the perpetuity formula that the total amount required when the dividend is paid for an innumerable time frame.
We know the formula of perpetuity is theoretical in nature, it can be understood with the following example.
In case of a real estate deal when one person purchases a property and gives it for rent then the owner is entitled to earning which is infinite in nature or in other words the income from rent is expected to come for an infinite time frame. We suppose that the property would last for an infinite time.
Significance and use of perpetuity Formula
One of the contradictions of perpetuity formula is its value which is infinite in nature.
There might be an argument regarding finite valuation of particular cash flow for an infinite time frame. The answer can be given like this
as the future cash flow keeps on falling because of the inflation rate the present values are high in the early years and the value of the perpetuity continuous to fall with time. Does the real value of payments tend to decrease over time? Thus, the very distant future will have a valuation which will be equivalent to zero but it won’t be the same value of zero. Therefore we make calculate the value of infinite series with the formula of perpetuity.
In corporate finance, the value of a different stream of cash flows differs in course of time. Perpetuity is nothing but a stream of cash flows that never ends. So if we purchase perpetuity it means that its repayment would last till the end of time.
Considering the example of common stock we notice that the dividend received by the stockholders is infinite therefore the equity holder is getting an infinite stream of future dividend against the purchase of equity shares.
The same goes for the students who are given a scholarship. As the scholarship is paid for a fixed number of years but the results of the philanthropic activities are believed to lasts for infinite future.
Perpetuity Calculator
You can use the following Perpetuity Calculator
| D | |
| R | |
| PV of Perpetuity Formula = | |
| PV of Perpetuity Formula = |
|
|
Perpetuity Formula in Excel (With Excel Template)
Here we will do the same example of the Perpetuity formula in Excel. It is very easy and simple. You need to provide the two inputs i.e Dividend and Discount Rate
You can easily calculate the Perpetuity using Formula in the template provided.
Conclusion
The general assumptions which are taken into account in case of Perpetuity are that the time frame is infinite. But in practice, there is a finite value for the perpetuity’s current value which is accrued in nature and is expected to deliver a return which has low value due to the inflation which is taken into account.
However, there might be a situation where the value of the perpetuity can change over a period of time including the same number of payment. This generally happens due to the change in discount or coupon rate. The value of perpetuity increases with a decrease of coupon rate and vice-versa.
Recommended Articles
This has been a guide to a Perpetuity formula. Here we discuss its uses along with practical examples. We also provide you with Perpetuity Calculator with downloadable excel template. You may also look at the following articles to learn more –
