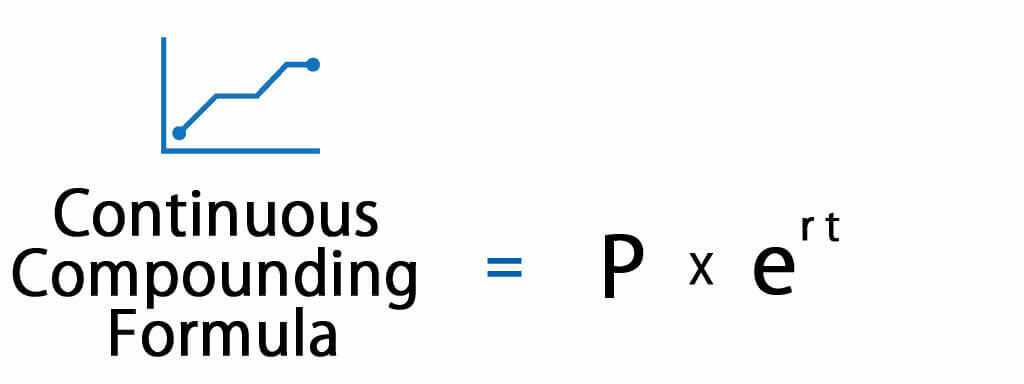Continuous Compounding Formula (Table of Contents)
- Continuous Compounding Formula
- Continuous Compounding Calculator
- Continuous Compounding Formula in Excel (With Excel Template)
Continuous Compounding Formula
Before jumping to continuous compounding concept, let’s understand what is compounding interest first. Compounding interest means the interest investors earn each year is added to his principal, so that the amount doesn’t only grow, it grows at an increasing rate than simple interest rate – is one of the most useful concepts in finance. It is the basis of everything from a long-term investment plan in share market to the personal savings plan. It also takes care of the effects of inflation on the amount, and the importance of paying debtOverhead Ratio Formula | Calculator (Excel template).
For continuously compounding interest rate gets added on every moment. This makes calculation tough. This is not used by any financial institution for interest rate charges as there is little difference in continuously compounding amount and daily compounding amount. Banks use daily compounding interest amount in some of their products.
The formula for continuous compounding is as follow:
The continuous compounding formula calculates the interest earned which is continuously compounded for an infinite time period.
where,
P = Principal amount (Present Value of the amount)
t = Time (Time is years)
r = Rate of Interest.
The above calculation assumes constant compounding interest over an infinite time period. As the time period mentioned is infinite, the exponent function (e) helps in a multiplication of the current investment amount. This is multiplied by the current interest rate and time period. In spite of a large number of investments amount, a difference between total interest earned through continuous compounding in excel is the same as compared with traditional compounding interest.
Examples & Explanation of Continuous Compounding Formula
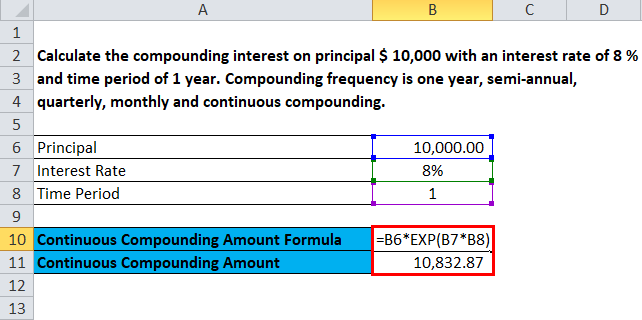
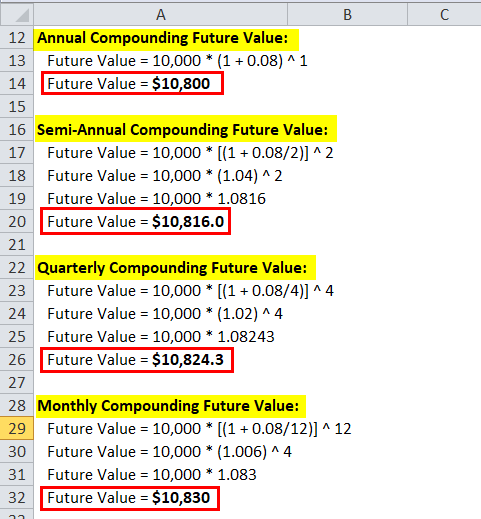
Calculate the compounding interest on principal $ 10,000 with an interest rate of 8 % and time period of 1 year. Compounding frequency is one year, semi-annual, quarterly, monthly and continuous compounding.
Annual Compounding Future Value:
- Future Value = 10,000 * (1 + 0.08) ^ 1
- Future Value = $10,800
Semi-Annual Compounding Future Value:
- Future Value = 10,000 * [(1 + 0.08/2)] ^ 2
- Future Value = 10,000 * (1.04) ^ 2
- Future Value = 10,000 * 1.0816
- Future Value = $10,816.0
Quarterly Compounding Future Value:
- Future Value = 10,000 * [(1 + 0.08/4)] ^ 4
- Future Value = 10,000 * (1.02) ^ 4
- Future Value = 10,000 * 1.08243
- Future Value = $10,824.3
Monthly Compounding Future Value:
- Future Value = 10,000 * [(1 + 0.08/12)] ^ 12
- Future Value = 10,000 * (1.006) ^ 4
- Future Value = 10,000 * 1.083
- Future Value = $10,830
Continuous Compounding Future Value:
- Future Value = 10,000 * e 0.08
- Future Value = 10,000 * 1.08328
- Future Value = $10,832.87
As it can be seen from the above example of calculations of compounding with different frequencies, the interest calculated from continuous compounding is $832.9 which is only $2.9 more than monthly compounding. So it makes case of using monthly or daily compounding interest rate in practical life than continuous compounding interest rate.
4.8 (956 ratings)
View Course
Significance and Use of Continuous Compounding Formula
The importance of continuous compounding formula is:
- Instead of continuous compounding of interest on an annual basis, quarterly basis or monthly basis, continuous compounding excel will efficiently reinvest gains over perpetually.
- The continuous compounding effect allows the continuous compounding of interest amount to be reinvested at same interest rate thereby give an opportunity to an investor to earn returns at an exponential rate.
- Continuous compounding determines that it is not only the principal amount which will earn money but also the continuous compounding of interest amount will also keep on multiplying the amount.
Compounding can be done on annual basis, semi-annual basis, quarterly basis, daily basis or continuous basis. Difference between these time periods is, after finishing the time period whatever interest is earned is treated as new principal. For example, if compounding frequency is semi-annual then, interest will be added to principal after six months, this cycle continues till the maturity. Same is the case with another time frame, for annual interest gets added after a year, for quarter interest gets added after three months, for daily interest gets added on next day.
Continuous Compounding Calculator
You can use the following Continuous Compounding Calculator
| P | |
| r | |
| t | |
| Continuous Compounding Formula = | |
| Continuous Compounding Formula = | P x e(r x t) |
| = | 0 x e(0 x 0) = 0 |
Continuous Compounding Formula in Excel (With Excel Template)
Here we will do the same example of the Continuous Compounding formula in Excel. It is very easy and simple. You need to provide the three inputs i.e Principal amount, Rate of Interest and Time.
You can easily calculate the Continuous Compounding using Formula in the template provided.
First, we need to calculate Continuous Compounding amount using Formula
then, we need to compute the effects of the same on regular compounding:
Recommended Articles
This has been a guide to a Continuous Compounding formula. Here we discuss its uses along with practical examples. We also provide you with Continuous Compounding Calculator with downloadable excel template. You may also look at the following articles to learn more –
