Updated July 21, 2023
What is Modified Duration?
Modified Duration conveys the impact of change in interest rate on the change in the price of the security, therefore, it simply tries to calculate the percentage change in the price of the security that is caused by a percentage change in the interest rates of that security, and so, we can conclude that it is a slope variable or the first differential of the price with respect to interest rate.
Formula to Calculate Modified Duration
As explained above, the duration is the slope of the price to yield curve which shows the price of the bond as a function of the yield. So under this circumstance, the formula for the modified duration is as follows:
Where,
- P: Price of the Bond or the Value of a Portfolio of Bonds
- dP: Percentage Change in Price
- dr: Percentage in Yield
The above formula is applicable when the yield is continuously compounded. However, in actual practice, the yield is mostly semi-annually compounded, and therefore we need to adjust the above formula as per the following steps:
1. Find the price of the bond:dP
- Price of the Bond is the sum of the discounted coupons and the discounted par value to be received at the time of maturity.
- The formula for the computation of price as described in point a is as follows:
- Price = ((Coupon Rate/2 * Par value) / (1+Yeild/2)2*0.5) + ((Coupon Rate/2 * Par value) / (1+Yeild/2)2*1) + … + ((Coupon Rate/2 * Par value) / (1+Yeild/2)2*n) + Par value/ (1+Yeild/2)2*n)
- Here n: maturity
2. Apply the Modified duration formula on the price arrived above:
- Modified Duration = – (1/P) * (dP/dr)
- Using the rules of algebra,
- Modified Duration = (1 /(1+Yield/2)) * weighted average of the cash flow maturities
- Weighted average of cash flow maturities = Macaulay duration
3. Reducing the Modified duration formula to a function of Macaulay duration:
- Modified Duration = Macaulay Duration / (1+ (yeild/2))
- Macaulay Duration = Sum of the PV of CF of bond * T / Market Price of Bond
- T = Time to Maturity at the time of each cash flow
4. These calculations are not limited to only semi-annual compounding but also any other form of discrete compounding such as quarterly or monthly and so one.
Explanation
- We know that the interest rate and price of a bond are inversely related and if we draw a price to yield curve, the line that is tangent to the curve implies the duration of the security.
- So from the duration number, we are able to understand how much change will a 1% change in the interest rate or the yield bring in the price of the security.
- If yield increases, the price of the bond will decrease and vice versa and the magnitude of this decrease is known as modified duration or simply duration.
Example of Modified Duration(With Excel Template)
Let’s take an example to understand the calculation in a better manner.
Example #1
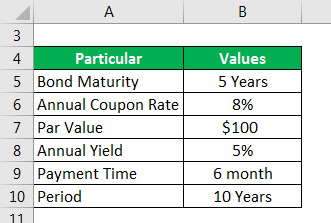
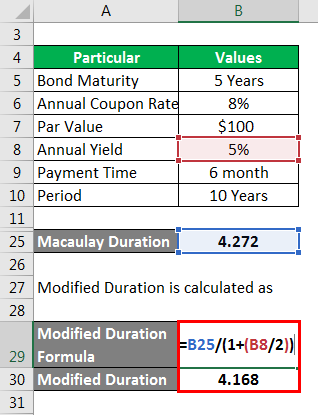
Applying the concept and formula discussed above to an example would lead to a better understanding of the concept. Suppose we are given the following information:
- Period = number of coupon periods, as there are semi-annual coupons so, in 5 years, there will be 5 x 2 = 10 coupon periods
- Payment time is every 6 months
Solution:
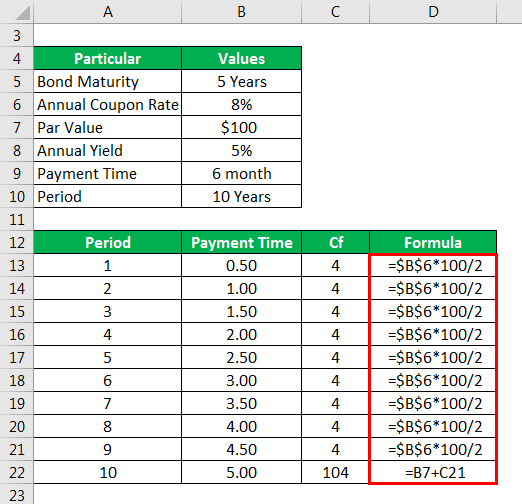
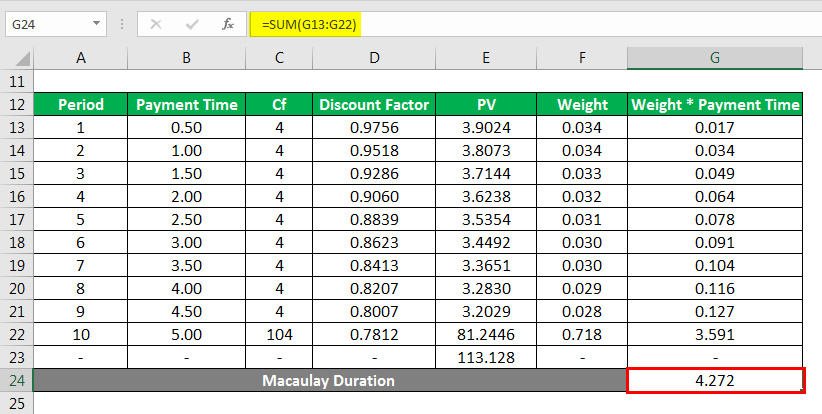
Cf is calculated as
- Cf = Annual Coupon Rate x Par Value/2
- Cf = 0.08 x 100/2
- Cf = 4
- In the 5th year the last CF = coupon + par value and therefore equals 100+4 = 104
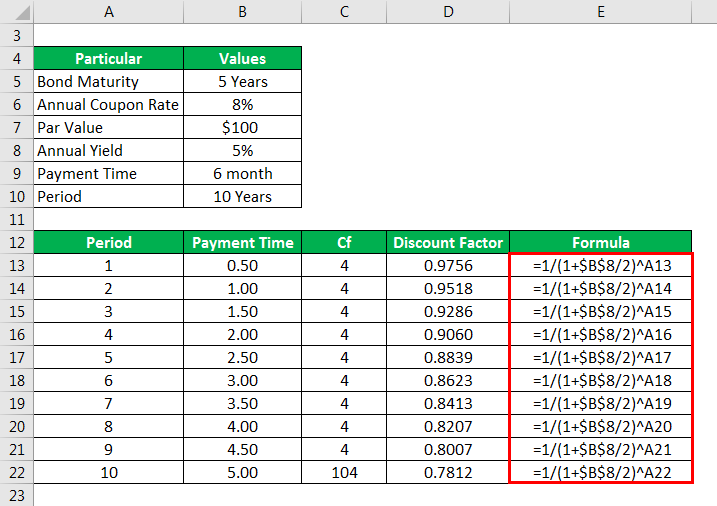
Discount Factor is calculated as
- Discount Factor = 1/(1+(Yield/2))Period
- Discount Factor for period 1 or payment time 0.5 = 1/(1+5%/2)Period = 0.9756
- All other discount factors are calculated by substituting the corresponding period in the above formula
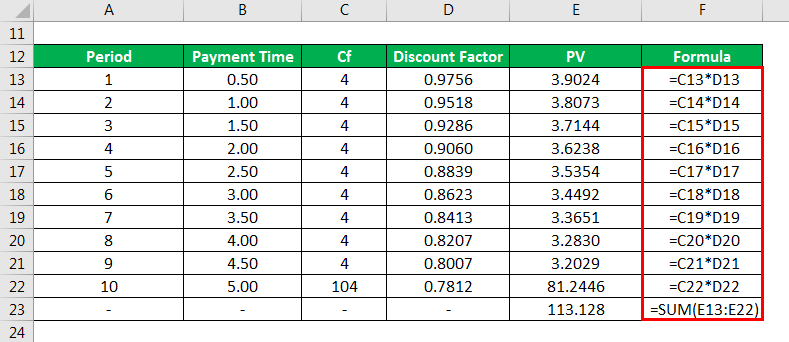
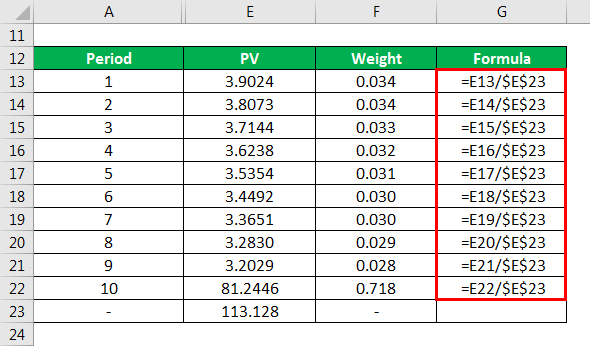
PV is calculated as
- PV= CF x Discount factor
- PV= 4 x 0.976 = 3.902
- All other PV values are computed by multiplying the Cf with their corresponding discount factor.
Price = Sum of all PV = 113.128
Weight is calculated as
- Weight = PV/Price
- Weight of CF at period 1 or payment time 0.5 = 3.902/113.128 = 0.034
- Similarly, all other weights are calculated
Macaulay Duration is calculated as
- Macaulay Duration = sum of all the weigh x time values
- Macaulay Duration = 4.272
Modified Duration is calculated as
- Modified Duration = 4.272/(1+0.05/2)
- Modified Duration = 4.168
This implies that if there is a 1% change in the yield, there will be a 4.168% change in the price
Modified Duration vs Macaulay Duration
- As shown in the above example, the Macaulay duration is the weighted average of cash flow maturities while the modifies duration requires further adjustments to Macaulay duration
- Macaulay duration is used to understand that for how long an investor needs to hold a bond for the present value of the CFs to equal the price paid for the bond. Therefore it is a measure of by when will the investment in the bond be recovered. In contrast, the modified duration shows how will a bond’s price change to a change in the yield for the bond.
- Macaulay duration is useful to portfolio managers in understanding till when the portfolio remains invested in a bond, while the modified duration helps them in understanding how will a bond portfolio react to an upcoming movement in the interest rates and thus adjust the proportion of bond investments accordingly.
Advantages and Disadvantages
Below we will learn about Modified Duration:
Advantages
- Determinant of Interest Rate Risk: Investors can use Duration as a metric to see what level of interest rate risk they want to bear. This can help them in selecting the most appropriate bond from a large pool of available bonds
- Planning: Investors also use duration to plan their timing in and out of the investment. If they foresee that the interest rate risk is becoming too high, they would want to get out of the investment. Therefore duration helps them in planning and timing their portfolios
Disadvantages
- Approximate Measure: As we have explained that the duration is the first-order differential of the Price-yield curve and therefore the tangent line to the same, however, the price to yield curve is convex to the origin and therefore duration only captures the impact of change in interest rates on price approximately. Convexity captures the same in a much better manner
- Complex Bonds: Duration is not a highly effective measure for complex bonds such option embedded ones, therefore the pool of bonds that can be analyzed using duration is limited
Conclusion
Duration measures the sensitivity of a security to the movement in the interest rates and can be used in planning the investments of a portfolio of securities. Duration has several variants such as Macaulay duration, modified duration and Effective duration, each having its own usefulness. Modified duration is a popular metric among portfolio managers. In spite of it being a popular metric, it is flawed as it doesn’t incorporate the convexity of the relationship of price and yield and therefore is only an approximate measure.
Recommended Articles
This is a guide to Modified Duration. Here we discuss how to calculate the along with practical examples along with downloadable excel template. You may also look at the following articles to learn more –