Updated July 26, 2023
Effective Annual Rate Formula (Table of Contents)
What is the Effective Annual Rate Formula?
Effective Annual Rate is the actual interest rate that is earned or paid out on an investment, loan, or any similar financial product, and it is otherwise different from “nominal Interest Rate” because of the payout period of interest, compounding of interest rate, total time period of the loan or investment, etc.
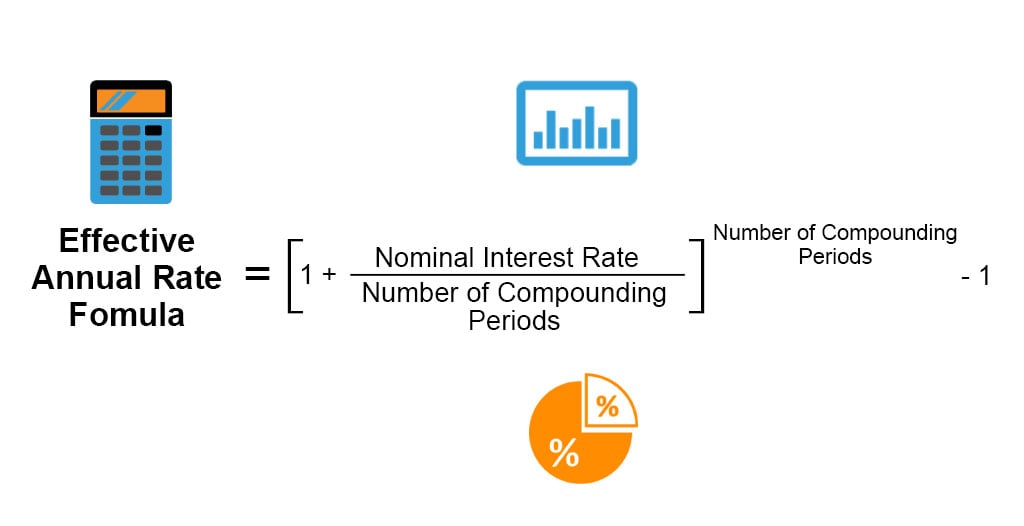
The following formula calculates the effective Annual Rate;
Examples of Effective Annual Rate Formula (With Excel Template)
Let’s take an example to understand the calculation of the Effective Annual Rate in a better manner.
Example #1
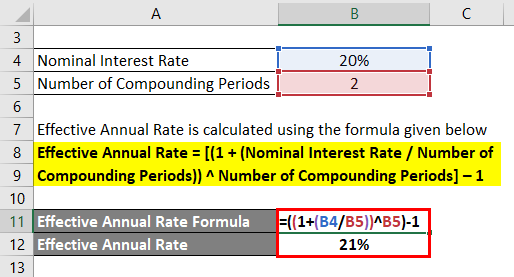
Suppose Mr. X takes out a personal loan from a bank with an interest rate of 20%, compounded semi-annually. Calculate the Effective Annual Rate using the information.
Solution:
The formula to calculate the Effective Annual Rate is as below:
Effective Annual Rate = [(1 + (Nominal Interest Rate / Number of Compounding Periods)) ^ Number of Compounding Periods] – 1
- Effective Annual Rate = [(1 + (20% / 2)) ^ 2] – 1
- Effective Annual Rate = 21%
Example #2
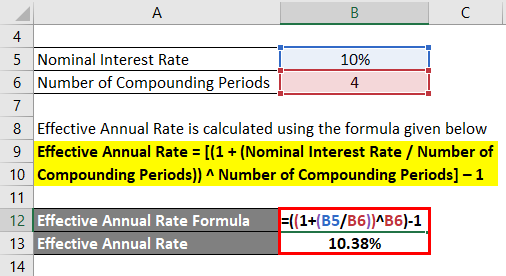
Suppose Mr. A invested $100 in a certificate of deposit that pays out a nominal annual interest rate of 10% compounded on a quarterly basis. Calculate the Effective Annual Rate.
Solution:
The formula to calculate the Effective Annual Rate is as below:
Effective Annual Rate = [(1 + (Nominal Interest Rate / Number of Compounding Periods)) ^ Number of Compounding Periods] – 1
- Effective Annual Rate = [(1 + (10% / 4)) ^ 4] – 1
- Effective Annual Rate = 10.38%
Example #3
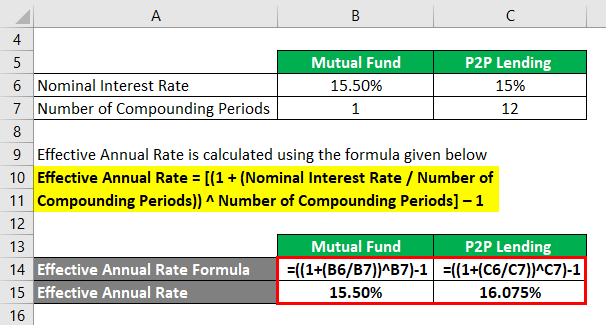
Let us assume that mutual fund investment fetches a 15.50% annual interest rate as earnings, while P2P Lending earns a 15% annual nominal interest rate, compounded monthly. To calculate the effective annual rate for both cases.
Solution:
The formula to calculate Effective Annual Rate is as below:
Effective Annual Rate = [(1 + (Nominal Interest Rate / Number of Compounding Periods)) ^ Number of Compounding Periods] – 1
For Mutual Fund
- Effective Annual Rate = [(1 + (15.50% / 1)) ^ 1] – 1
- Effective Annual Rate = 15.50%
For P2P Lending
- Effective Annual Rate = [(1 + (15% / 12)) ^ 12] – 1
- Effective Annual Rate = 16.075%
Explanation
The nominal interest rate is the stated rate on the financial product. In Example 3, the nominal rate displayed on the products makes the Mutual Fund look like the preferred investment choice for investors because of the 0.50% higher annual nominal rate of interest earned.
However, the effective annual rate is calculated by taking the nominal annual rate of interest and compounding it for the number of specified periods (12 if compounding is monthly; 6 if compounding is bi-monthly; 4 if it is quarterly; and 2 if it is semi-annual) applicable in a time span of one year. In the case of the mutual fund, the number of compounding periods per year is 1, while in the case of P2P lending, it is monthly compounding. Hence there are 12 compounding periods.
Based on the formula,
Mutual Fund Effective Annual Return = [(1 + (15.50% / 1)) ^ 1] – 1 = 15.50%
P2P Lending Effective Annual Return = [(1 + (15.00% / 12)) ^ 12] – 1 = 16.075%
Relevance and Uses of Effective Annual Rate Formula
The effective annual rate formula distinguishes the actual IRR (Internal Rate of Return) or annualized yield for an interest rate that may or may not compound multiple times over a given period. This could be very well used in comparing different kinds of investment opportunities or loan facilities taken under different structures.
Let us assume that there are 2 investment opportunities, Post Office Term Deposits and Bank Fixed Deposits, that an investor has narrowed down to, considering his/her risk appetite and suitability. The investor’s ultimate goal is to make the most of these deposits and earn a higher return. However, both instruments offer slightly different interest rates, while the Post Office Term Deposit offers quarterly compounding for the term under consideration.
- Investment Amount: Rs. 10 lakhs
- Period of Investment: 5 years
- Bank Fixed Deposit: 7.5% Annual Interest
- Post Office Term Deposit: 7.4% Annual Interest, compounded quarterly
The Bank Fixed Deposit seems to be the better option by looking at the annual interest rates offered. However, if the investor calculates the quarterly compounding factor of the Post Office Term Deposit, it results in an effective annual rate/return of 7.61%.
Due to this small change from 7.4% to 7.61% in effective rate, the investor would earn a total of Rs. 4,42,848.28 from this particular instrument, whereas he/she would have earned Rs. 3,35,469.14 from the Bank Fixed Deposit instrument.
If the investor misses calculating this effective annual rate, he/she will have lost the opportunity to gain approximately more than Rs. 1 lakh from his investment.
Effective Annual Rate Formula Calculator
You can use the following Effective Annual Rate Calculator
| Nominal Interest Rate | |
| Number of Compounding Periods | |
| Effective Annual Rate | |
| Effective Annual Rate = | [(1 + (Nominal Interest Rate / Number of Compounding Periods))Number of Compounding Periods] - 1 | |
| [(1 + (0 / 0))0] - 1 = | 0 |
Recommended Articles
This is a guide to Effective Annual Rate Formula. Here we discuss How to Calculate Effective Annual Rates and practical examples. We also provide an Effective Annual Rate Calculator with a downloadable Excel template. You may also look at the following articles to learn more –