Updated July 24, 2023
Modified Duration Formula (Table of Contents)
What is the Modified Duration Formula?
The term “Modified Duration” refers to a metric that helps in assessing the expected change in the value of security due to a change in the prevailing interest rates. In other words, modified duration measures a bond’s sensitivity to changes in interest rate.
The formula for the modified duration is expressed as Macaulay duration (a.k.a. just “duration”) divided by one plus effective yield to maturity (YTM). The mathematical representation of the formula is as below:
Where
- n: Number of Coupon Periods per Year
Please note that Macaulay duration can be computed using the following formula,
Where,
- C: Coupon Payment per Period
- M: Par Value
- t: Number of Periods until Maturity
Example of Modified Duration Formula (With Excel Template)
Let’s take an example to understand the calculation of Modified Duration in a better manner.
Modified Duration Formula – Example #1
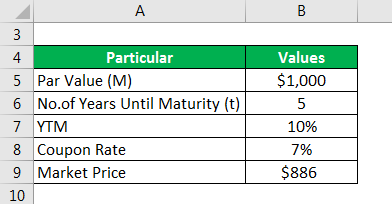
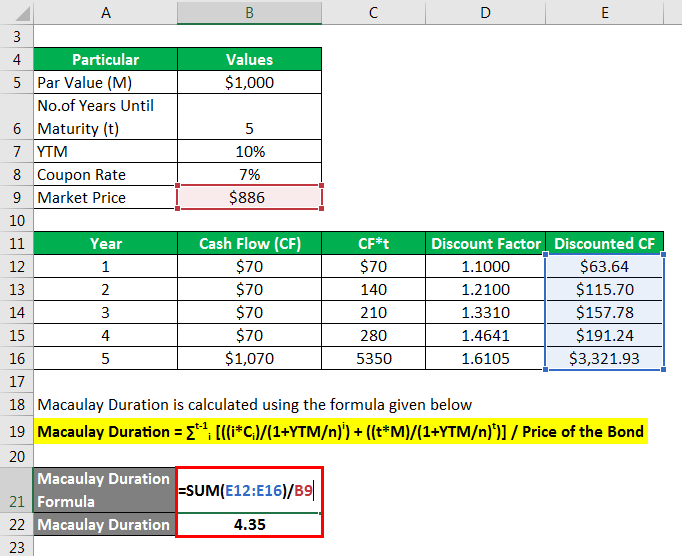
Let us take the example of a security that pays an annual coupon of 7%. The par value of the 5-year security is $1,000, and its current market price is $886. Calculate the modified duration of the security if the YTM is 10%.
Solution:
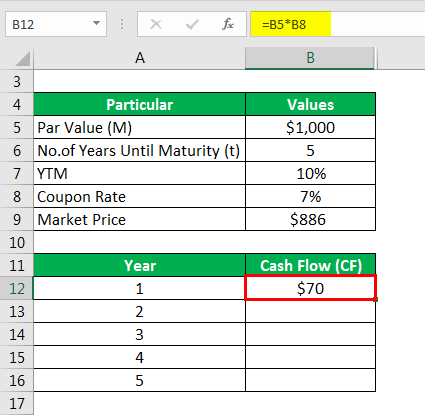
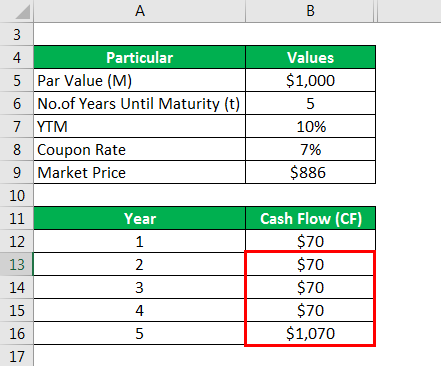
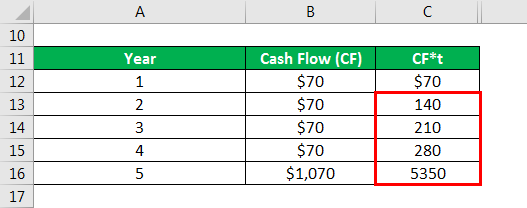
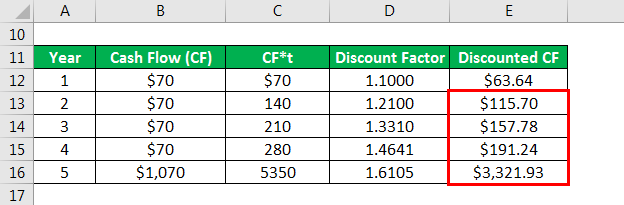
Calculate cash flow as
Similarly, calculated as below
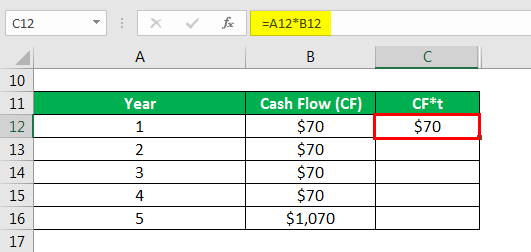
Calculate cf*t as
Similarly, calculated as below
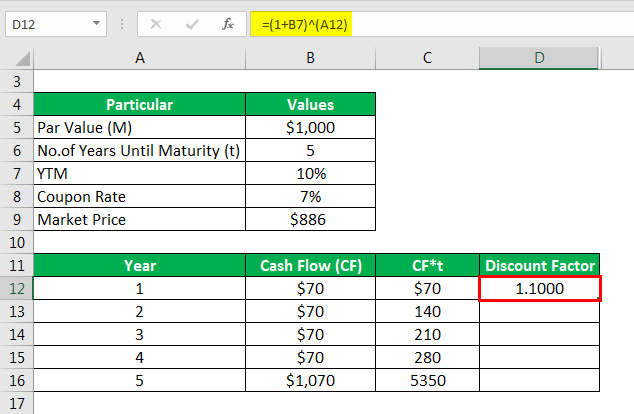
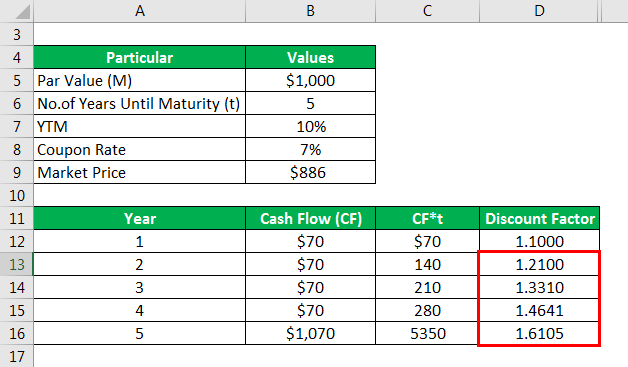
Calculate Discount Factor as
Similarly, calculated as below
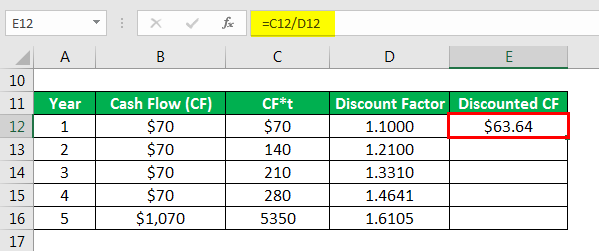
Calculates discounted CF as
Similarly, calculated as below
The formula to calculate Macaulay Duration is as below:
Macaulay Duration = ∑t-1i [((i*Ci)/(1+YTM/n)i) + ((t*M)/(1+YTM/n)t)] / Price of the Bond
- Macaulay Duration= [ 70*1/(1+10%)1+ 70*2/(1+10%)2 +70*3/(1+10%)3 + 70*4/(1+10%)4 +1070*5/(1+10%)5] / 886
- Macaulay Duration = 4.35
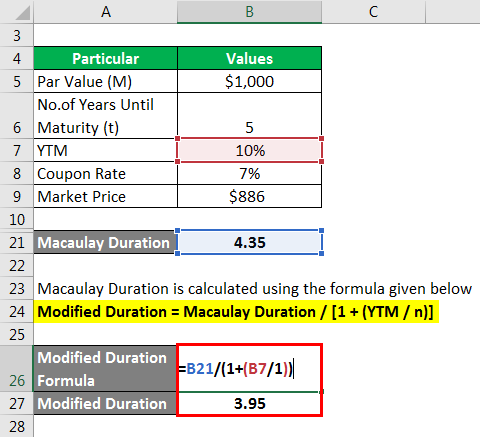
The formula to calculate Macaulay Duration is as below:
Modified Duration = Macaulay Duration / [1 + (YTM / n)]
- Macaulay Duration = 4.34 / [1 + 10%]
- Macaulay Duration = 3.95
Therefore, for every 1% change in interest rate, the price of the security would inversely move by 3.95%.
Modified Duration Formula – Example #2
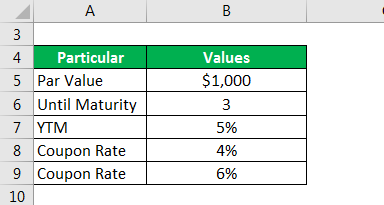
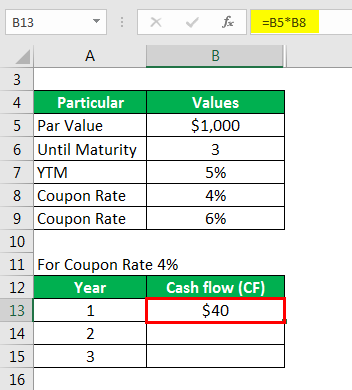
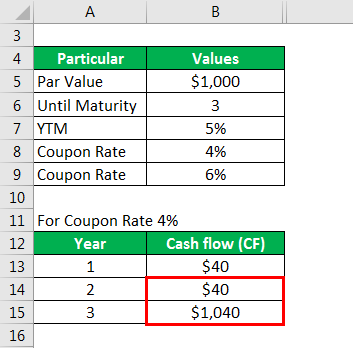
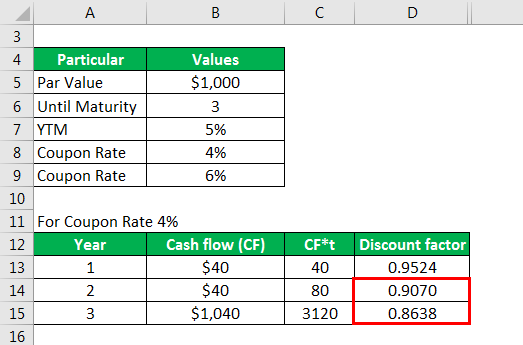
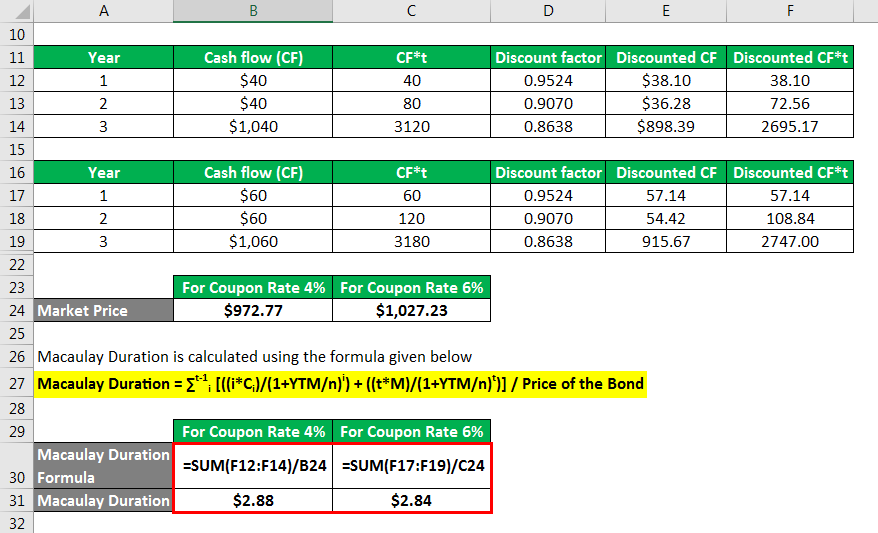
Let us take the example of a 3-year coupon paying bond with a par value of $1,000. If the YTM for the bond is 5%, then calculate the bond’s modified duration for the following annual coupon rate: 4% and 6%.
Solution:
Calculate cash flow as
Similarly, calculated as below
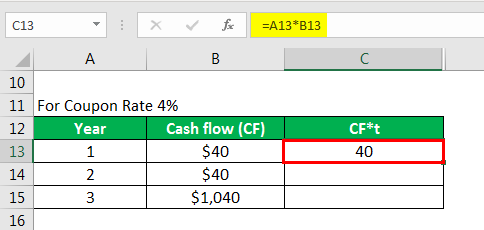
Calculate cf*t as
Similarly, calculated as below
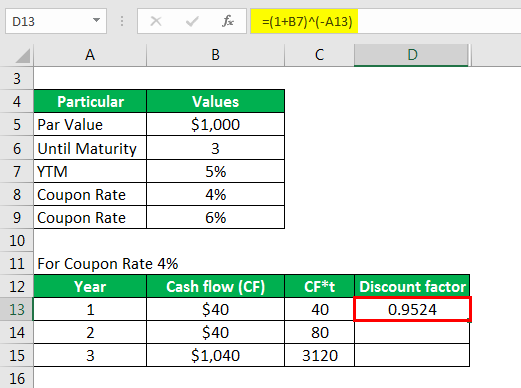
Calculate Discount Factor as
Similarly, calculated as below
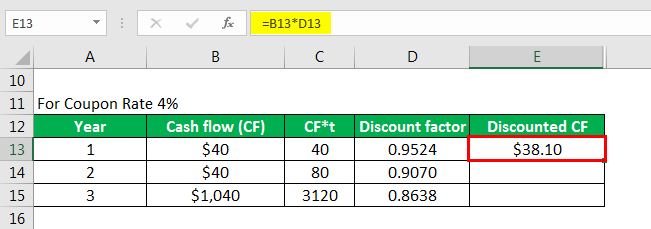
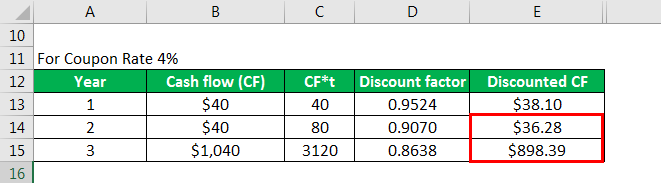
Calculates discounted CF as
Similarly, calculated as below
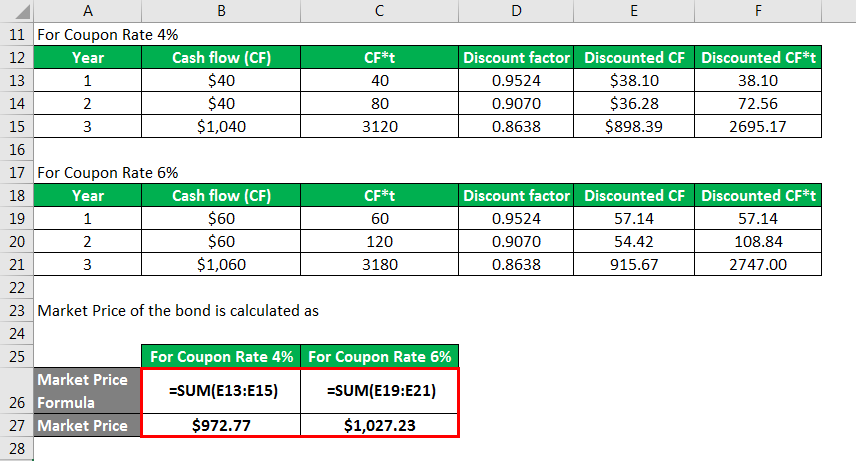
Similarly done for For Coupon Rate 6%.
Market Price of the bond calculation:
For Coupon Rate 4%
- Market Price = $40/(1+5%)1 + $40/(1+5%)2 + $1,040/(1+5%)3
- Market Price = $972.77
For Coupon Rate 6%
- Market Price = $60/(1+5%)1+ $60/(1+5%)2 + 1060/(1+5%)3
- Market Price = $1,027.23
The formula to calculate Macaulay Duration is as below:
Macaulay Duration = ∑t-1i [((i*Ci)/(1+YTM/n)i) + ((t*M)/(1+YTM/n)t)] / Price of the Bond
For Coupon Rate 4%
- Macaulay Duration = [ 40*1/(1+5%)1+40*2/(1+5%)2 +1040*3/(1+5%)3 ] / 972.77
- Macaulay Duration = 2.88
For Coupon Rate 6%
- Macaulay Duration = [ 60*1/(1+5%)1+ 60*2/(1+5%)2 + 1060*3(1+5%)3 ] / 1,027.23
- Macaulay Duration = 2.84
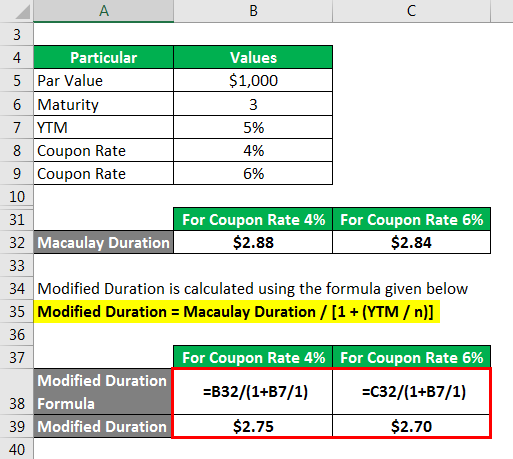
The formula to calculate Modified Duration is as below:
Modified Duration = Macaulay Duration / [1 + (YTM / n)]
For Coupon Rate 4%
- Modified Duration = 2.88 / [1 + 5%]
- Modified Duration = 2.75
For Coupon Rate 6%
- Modified Duration = 2.84 / [1 + 5%]
- Modified Duration = 2.70
Therefore, it can be seen that the modified duration of a bond decreases with the increase in the coupon rate.
Explanation
The formula for Modified Duration can be calculated by using the following steps:
Step 1: Firstly, determine the YTM of the security based on its current market price
Step 2: Next, determine the number of compounding per year or coupon periods per year, denoted by n.
Step 3: Next, compute the Macaulay security duration based on its par value on maturity, current market price, coupon payment per period, YTM, number of coupon periods per year, and periods until maturity.
Step 4: Finally, the formula for the modified duration of the security can be derived by dividing its Macaulay duration (step 3) by one plus YTM (step 1) divided by the number of coupon periods per year (step 2), as shown below,
Modified Duration = Macaulay Duration / [1 + (YTM / n)]
Relevance and Use of Modified Duration Formula
It is important to understand the concept of modified duration because it is useful to assess the sensitivity of the security to the change in the interest rate in the market. As such, bond investors closely check this metric whenever the interesting scenario is volatile. This metric is based on the basic principle that interest rates and bond prices move in opposite directions. So, it essentially shows that if the interest rate in the market moves by 1%, then the bond price would move by the value of modified duration in the opposite direction. For example 1, if the interest rate increases by 1%, then the security value would decrease by 3.95%.
Modified Duration Formula Calculator
You can use the following Modified Duration Formula Calculator
| Macaulay Duration | |
| YTM | |
| n | |
| Modified Duration | |
| Modified Duration = | Macaulay Duration / [1 + (YTM / n)] |
| = | 0 / [1 + (0 / 0)] = 0 |
Recommended Articles
This is a guide to Modified Duration Formula. Here we discuss how to calculate the Modified Duration along with practical examples. We also provide a Modified Duration calculator with a downloadable Excel template. You may also look at the following articles to learn more –