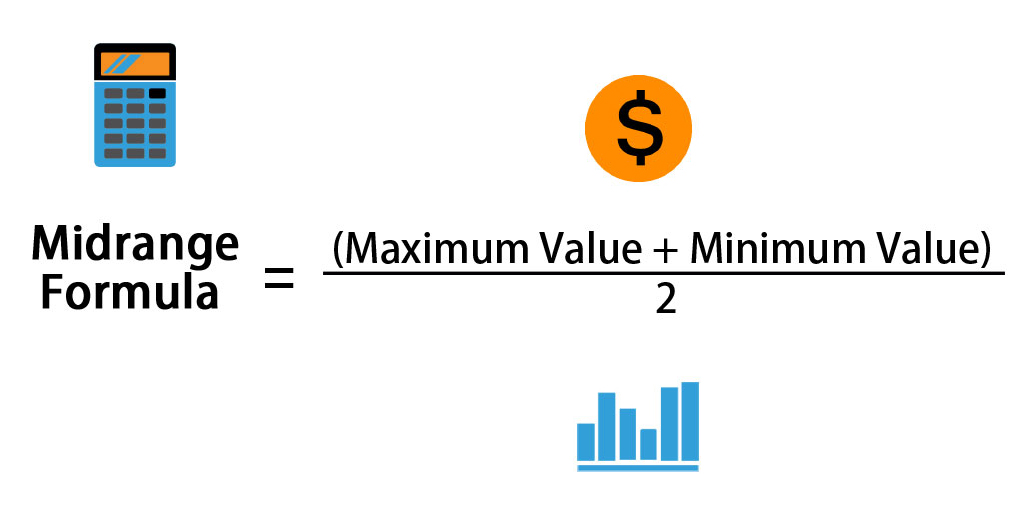Updated July 29, 2023
Midrange Formula (Table of Contents)
Midrange Formula
Midrange in layman terms is the middle of any data set or the simply the average, mean of the data. A midrange is a statistical tool which is also known as the measure of center in statistics.
Along with the existence of the midrange formula means, medium, average, mode, and range are also known as the measure of central tendency. The midrange of the data set is simply the value between the biggest value and the lowest value. In order to find the midrange of the data set the value is then divided by 2 after summing the lowest value present in the data set with the highest value present in the data set.
Today, In this article we will try and understand the working and the logic behind the working of the Midrange formula. And the relevance and the use of it. However, it is recommended by some statistician that in order to find the midrange of the data set we need to present the data in ascending and descending order. Since we are finding the midrange of the data set and we are picking the lowest and the highest value of the data so it is not necessary to arrange the present data in ascending and the descending order.
A formula for Midrange is given by:
Examples of Midrange Formula (With Excel Template)
Let’s take an example to understand the calculation of Midrange formula in a better manner.
Midrange Formula – Example #1
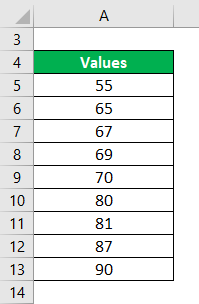
The daily temperature recorded in the city of Colombia Bogata is 55, 65, 67, 69, 70, 80, 81, 87, 90. We need to calculate the mid-temperature in Bogata during this period.
Solution:
Now we need to find the Midrange of the given function and how spread the data set is.
A Midrange of a given function can be calculated with the help of the following steps:-
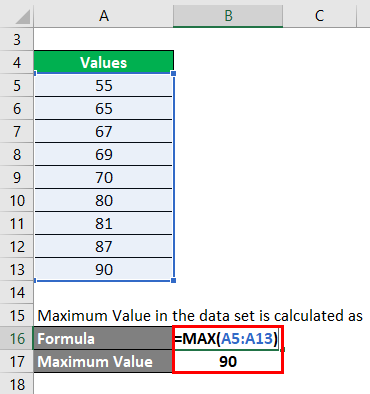
Step 1: First, we need to find what is the maximum value in the data set. Maximum Value in the data set is calculated as
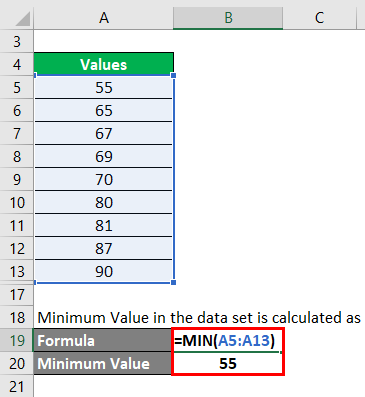
Step 2: Then we need to find what is the minimum value in the data set. Minimum Value in the data set is calculated as
Step 3: Midrange is calculated using the formula given below
Midrange = (Maximum Value + Minimum Value) / 2
- Midrange = (90 + 55) / 2
- Midrange = 145 / 2
- Midrange = 72.5
Midrange Formula – Example #2
The test scores of Mr. Nadal recorded in the state government entrance exam of Uttar Pradesh are 28, 33, 34, 35, 42, 40, 41, 44, 45. We need to calculate the midrange value.
Solution:
Now we need to find the Midrange of the given function and how spread the data set is.
A Midrange of a given function can be calculated with the help of the following steps:-
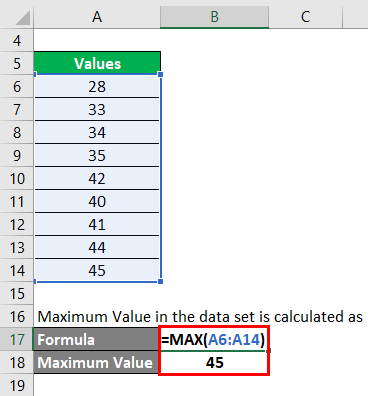
Step 1: First, we need to find what is the maximum value in the data set. Maximum Value in the data set is calculated as
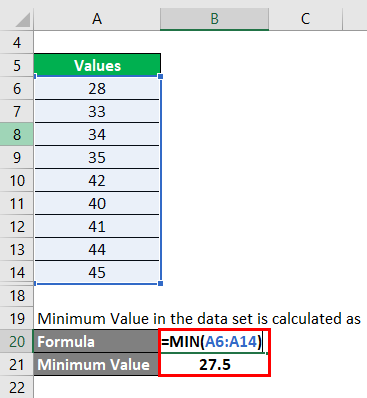
Step 2: Then we need to find what is the minimum value in the data set. Minimum Value in the data set is calculated as
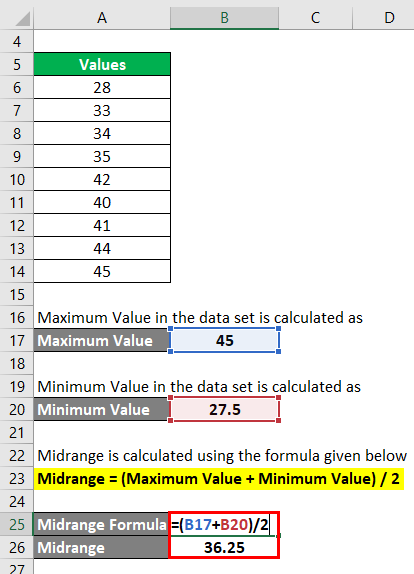
Step 3: Midrange is calculated using the formula given below
Midrange = (Maximum Value + Minimum Value) / 2
- Midrange = (45 + 27.5) / 2
- Midrange = 72.5
- Midrange = 36.25
Midrange Formula – Example #3
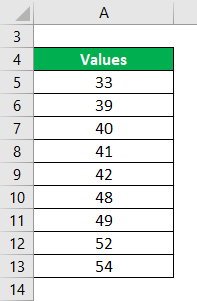
Here is the data set with numbers 33, 39, 40, 41, 42, 48, 49, 52, 54. We need to calculate the midrange.
Solution:
Now we need to find the Midrange of the given function and how spread the data set is.
A Midrange of a given function can be calculated with the help of the following steps:-
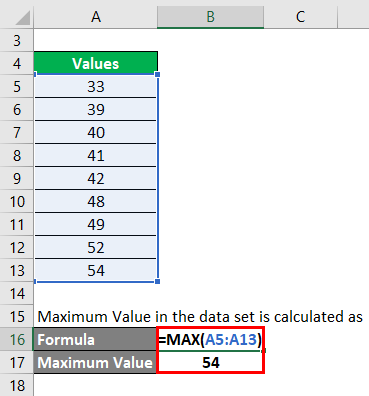
Step 1: First, we need to find what is the maximum value in the data set. Maximum Value in the data set is calculated as
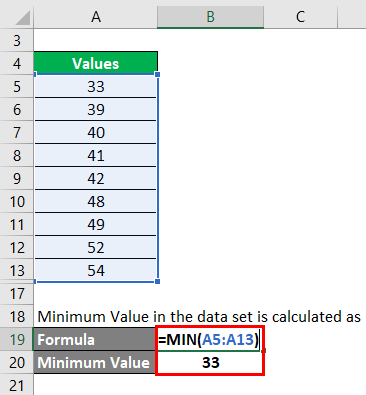
Step 2: Then we need to find what is the minimum value in the data set. Minimum Value in the data set is calculated as
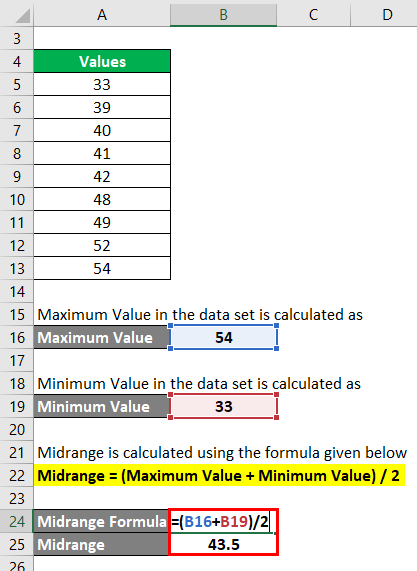
Step 3: Midrange is calculated using the formula given below
Midrange = (Maximum Value + Minimum Value) / 2
- Midrange = (54 + 33) / 2
- Midrange = 87 / 2
- Midrange = 43.5
Explanation
The formula for Midrange basically the average of the data set. The Midrange is being computed as the average of the maximum and the minimum values present in the data sample corresponds to the measure of central tendency.
The midrange Formula can be computed as –
Relevance and Uses of Midrange Formula
- The midrange formula of statistics is of great help when the user needs to find the midpoint of a large data set and it also provides as an alternative calculation for the measure of central tendency.
- It also tells us about the maximum and the minimum range of the data set and where most of the data lie in a particular array. It is also useful it finding averages of various data sets. However, Mean is the most popular statistical formula which is used most in the industry.
- The mid-range also lacks robustness, as outliers change it significantly. Indeed, it is one of the least efficient and least robust statistics.
Midrange Formula Calculator
You can use the following Midrange Calculator
| Maximum Value | |
| Minimum Value | |
| Midrange Formula = | |
| Midrange Formula = |
|
|
Recommended Articles
This has been a guide to Midrange Formula. Here we discuss how to calculate Midrange along with practical examples. We also provide Midrange calculator with downloadable excel template. You may also look at the following articles to learn more –