Updated July 29, 2023
Normal Distribution Formula (Table of Contents)
What is the Normal Distribution Formula?
The concept of the normal distribution is used in statistics, and we come across various kinds of distributions in statistics. One such distribution and the most often used distribution is the Normal Distribution which has the following characteristics:
- The mean, median, and the mode of the normal distribution are always equal.
- A normal curve is symmetric in nature.
- Half of the value lies on either side of the curve in a normal distribution, which is why it is called the bell-shaped curve.
A formula for Normal Distribution is given by:
- X = Value that is being standardized
- µ = Mean of the distribution
- ∞ = Standard deviation of the distribution
Examples of Normal Distribution Formula (With Excel Template)
Let’s take an example to understand the calculation of Normal Distribution in a better manner.
Normal Distribution Formula – Example #1
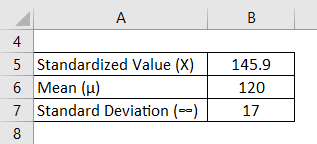
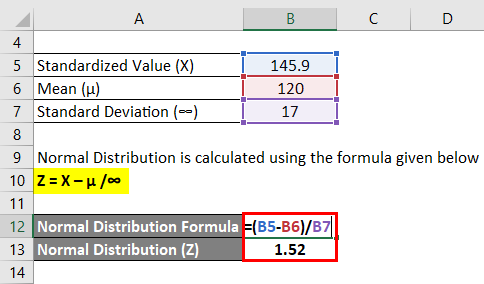
The X of an exam is given to be 145.9, and 30% of the students failed to pass the exam. The mean score of the test is 120, and the standard deviation is 17. What was the passing score of the test?
Solution:
Normal Distribution is calculated using the formula given below
Z = (X – µ) /∞
- Normal Distribution (Z) = (145.9 – 120) / 17
- Normal Distribution (Z) = 25.9 / 17
- Normal Distribution (Z) = 1.52
Normal Distribution Formula – Example #2
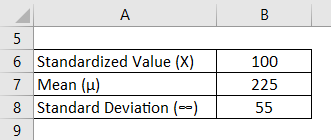
The monthly bill of water in the village of Hyderabad are normally distributed, and it has a mean of Rs. 225 and a standard deviation of Rs. 55. Those people spend a lot of their time in the fields watering the plant. In a group of 500 customers, how many customers can be expected to have a bill of Rs. 100 or less?
Solution:
Normal Distribution is calculated using the formula given below
Z = (X – µ) /∞
- Normal Distribution (Z) = (100 – 225) / 55
- Normal Distribution (Z) = -125 / 55
- Normal Distribution (Z) = -2.27
Normal Distribution Formula – Example #3
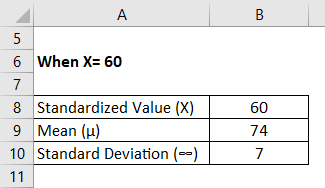
In an English test conducted in a classroom of 100 students, the score obtained by the students is normally distributed in the data set. However, the mean score of the test came out to be 74, and the standard deviation of 7. What proportion of the class is expected to have a score between 60 and 80?
Solution:
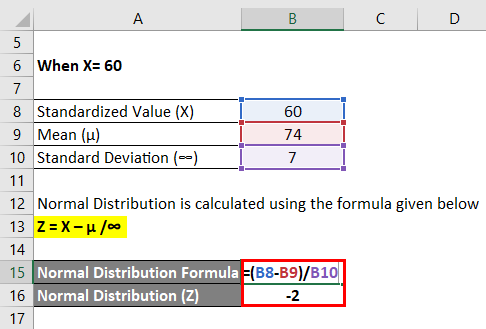
For X=60
Normal Distribution is calculated using the formula given below
Z = (X – µ) /∞
- Normal Distribution (Z) = (60 – 74) / 7
- Normal Distribution (Z) = -14 / 7
- Normal Distribution (Z) = -2
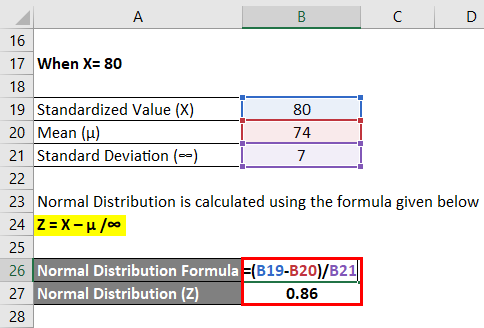
For X=80
Normal Distribution is calculated using the formula given below
Z = (X – µ) /∞
- Normal Distribution (Z) = (80 – 74) / 7
- Normal Distribution (Z) = 6 / 7
- Normal Distribution (Z) = 0.86
Explanation of Normal Distribution
Going to the formula in detail, a random variable that is being standardized is subtracted from the mean of the distribution and is then divided by the Standard deviation of the distribution. Once these terms are determined, we can simply compute the Z score, which is also known as the normal standard distribution.
Relevance and Uses of Normal Distribution Formula
- A normal distribution is used in statistics and in the natural sciences industry for the representation of the real-valued random variables.
- Normal distribution theory is also widely used in advanced sciences like astronomy, photonics, and quantum mechanics. Basically, it is a measure of the spread of the normal probability distribution.
- The theory of normal distribution is also widely used in the world of finance, where it is applied to the asset prices, and the deviation of the asset price from the mean or the median is judged, and the reason for such deviation is studied in detail.
- The normal distribution formula is also being used in the study of determining the skewness and the kurtosis of the probability distribution in a given form or nature. Although in reality, it is highly unlikely that most of the pricing distributions are normal in nature.
Normal Distribution Calculator
You can use the following Normal Distribution Calculator
| X | |
| µ | |
| ∞ | |
| Z | |
| Z = |
|
|
Recommended Articles
This has been a guide to the Normal Distribution Formula. Here we discuss how to calculate Normal Distribution along with practical examples. We also provide a Normal Distribution calculator with a downloadable excel template. You may also look at the following articles to learn more –