Updated July 27, 2023
Definition of Mean Example
Mean in statistical parlance refers to the mathematical arithmetic or geometric average, which can be calculated for a set of 2 or more timely returns.
However, as mentioned in the definition, there is more than a single way to calculate the average or the mean for a certain given set of data or given a set of numbers that shall include the methods of the geometric mean, and the arithmetic mean.
The equation or the formula for a mean or average of returns based on the arithmetic mean can be calculated by summing up all the available periodic returns or all the given observations and dividing that result by the number of observations or periods.
Examples of Mean
Below are examples of the mean:
Mean Example – #1
XYZ stock has been performing quite well for a couple of years. Still, the investors are a little skeptical about whether the stock will perform the same in the future as in recent weeks. Moreover, it has remained volatile as one of the company’s key personnel has resigned, and the market has started doubting its future.
Axel wants to invest in XYZ stock and has approached a financial advisor to advise on XYZ stock. Before deciding, the advisor calculates the mean of the weekly returns.
Solution:
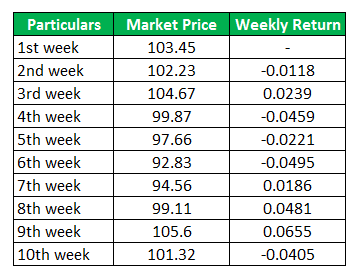
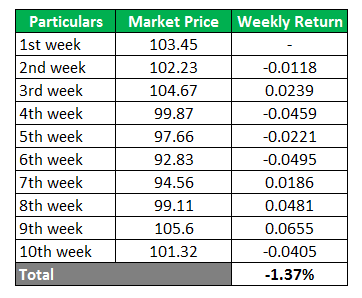
We are given weekly returns of the XYZ stock, and now we need to calculate the average of this weekly data for 9 weeks.
Here, the formula for computing the average or mean return is the sum of all data and dividing the same by several observations, and the Number of Observations is 9
Mean = Total / Number of Observations
Mean = -1.37% / 9
Mean = -0.15%
Hence, the mean weekly return would be -1.37%. Dividing the same by 9 will yield a -0.15% average return for XYZ stock.
Mean Example -2
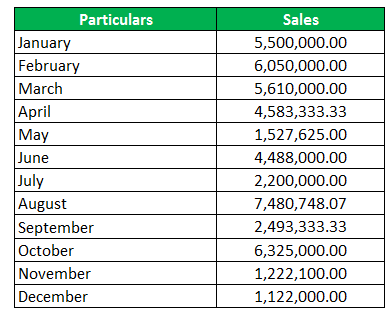
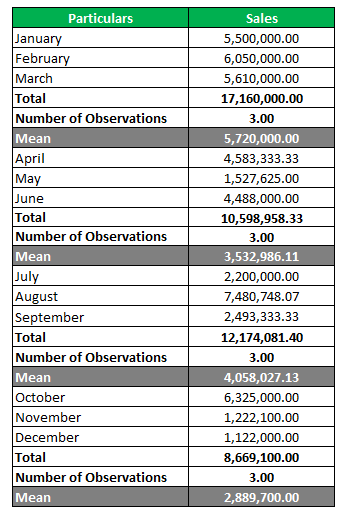
Suhas is the MD of Vatsal Enterprises, and he sees that his sales are variable every month. He wants to know the average quarterly sales and also identify the quarter in which the sales are the most.
Below are the monthly sales data extracted from accounting software. Now, you are required to compute the quarterly arithmetic average.
Solution:
We are given monthly sales, and therefore we will take the sum of 3 months starting from January, and then for each total, we will divide it by 3, which shall give us the quarterly average sales figure.
Mean = Total / Number of Observations
The highest average is for the 1st quarter; hence, that quarter is the best performing for the company.
Mean Example – #3
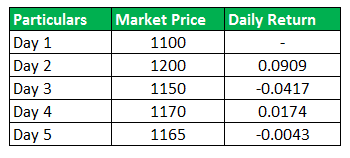
Jack Hemsley has recently graduated, and his field of interest lies in the stock market. He has been observing Alpha stock for quite some time and wants to calculate the average daily return as he feels he can now trade into the same and make some money. Likewise, Jill, his friend, advises him first to know what return he can expect when he starts trading; therefore, he suggests computing the average this stock has given. Jack decides to use a geometric average of over arithmetic average. Now, you have to compute the geometric mean on the below data for the last 5 days.
Solution:
To compute geometric return, we need to take the product of the return and then take the 4th root of the result and subtract the same from 1 will yield us the geometric return.
- Geometric mean = [ (1+0.0909) * (1-0.0417) * (1+0.0174) * (1-0.0043) ]1/4 – 1
- Geometric mean = 1.45%
Mean Example – #4
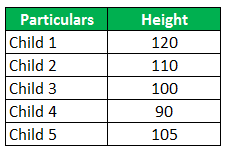
Consider the below height data of 5 children aged 10 years old. You have to compute both the arithmetic mean and geometric mean and compare both, and comment upon the same.
Solution:
To compute geometric return, we need to take the product of the observations and then take the 5th root of the result and subtract the same from 1 will yield us the geometric return.
- Geometric mean = [ (1+120) * (1+110) * (1+100) * (1+90) * (1+105) ]1/5 – 1
- Geometric mean = 104.52
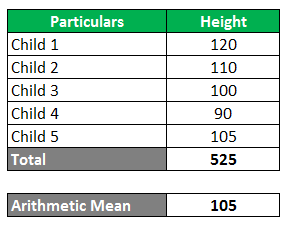
The formula for computing the average or mean return is the sum of all data and dividing the same by the number of observations, and the number of observations is 5.
Arithmetic Mean = Total / Number of Observations
- Arithmetic Mean = 525/5
- Arithmetic Mean= 105
The geometric mean is less than the arithmetic means and is generally the case, and it cannot be more than the arithmetic mean.
Conclusion
Average or mean is useful almost daily and for many reasons, especially in the capital market, science, statistics, etc. Using the appropriate average is the key. This matter is based upon an understanding of the data. The geometric average considers compounding, whereas the arithmetic average considers simple summation. Hence, Geometric is best where growth is known. An arithmetic average can be used when values are not much volatile and not much spread.
Recommended Articles
This article has been a guide to the Mean Example. Here we have discussed the Definition and various examples of Mean with Geometric and Arithmetic Mean. You may also have a look at the following articles to learn more –