Updated July 24, 2023
Marginal Utility Formula (Table of Contents)
What is the Marginal Utility Formula?
The term “Marginal Utility” refers to the satisfaction gained by a consumer on consuming an additional unit of a good or service. Basically, a consumer’s perceived total satisfaction or benefit changes for every additional unit of a good, i.e. it may increase until a certain point in time, and then the trend reverses.
The concept of marginal utility helps us in assessing this change in consumer perception in terms of different levels of satisfaction in a more scientific way (law of diminishing marginal utility).
The formula for marginal utility is expressed as a change in total utility (ΔTU) divided by the change in the number of units of the good or service consumed (ΔQ). Mathematically, it is represented as,
The above formula for marginal utility can also be expressed as,
Where,
- TUi: Total Utility at Qi Units
- TUf: Total Utility at Qf Units
- Qi: No. of Units Consumed Initially
- Qf: No. of Units Consumed Finally
Example of Marginal Utility Formula (With Excel Template)
Let’s take an example to understand the calculation of Marginal Utility in a better manner.
Marginal Utility Formula – Example #1
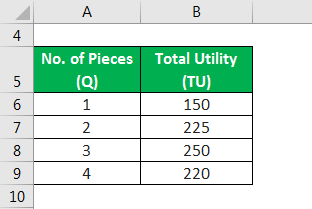
Let us take the example of John, who purchased a chocolate cake with 4 pieces. Now, the following information is available regarding his perceived utility after consumption of each piece of the cake. Calculate the marginal utility of each piece of the chocolate cake.
Solution:
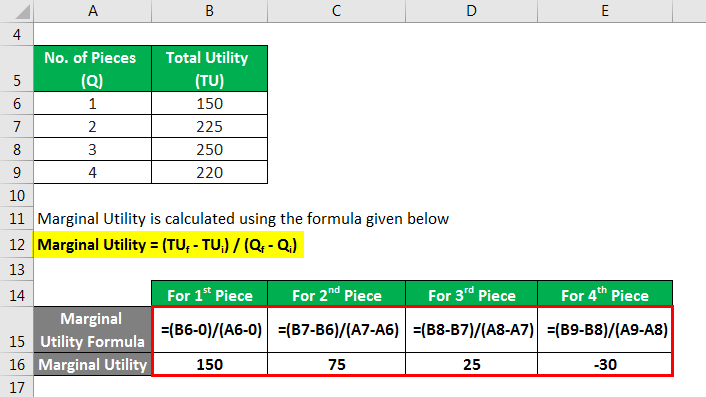
Marginal Utility is calculated using the formula given below
Marginal Utility = (TUf – TUi) / (Qf – Qi)
For 1st Piece of the Cake
- Marginal Utility1 = (150 – 0) / (1 – 0)
- Marginal Utility1 = 150
For 2nd Piece of the Cake
- Marginal Utility2 = (225 – 150) / (2 – 1)
- Marginal Utility2 = 75
For 3rd Piece of the Cake
- Marginal Utility3 = (250 – 225) / (3 – 2)
- Marginal Utility3 = 25
For 4th Piece of the Cake
- Marginal Utility4 = (220 – 250) / (4 – 3)
- Marginal Utility4 = -30
Therefore, here we can see how the marginal utility of a piece of cake declines after the consumption of the previous one. Here, the highest utility is reached at the consumption of the 3rd piece, beyond which the total declined. This is a classic example of diminishing marginal utility.
Marginal Utility Formula – Example #2
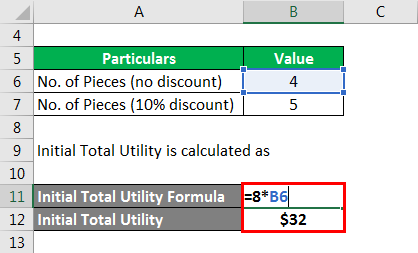
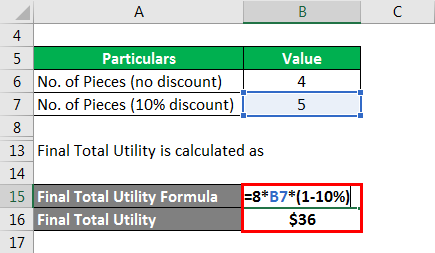
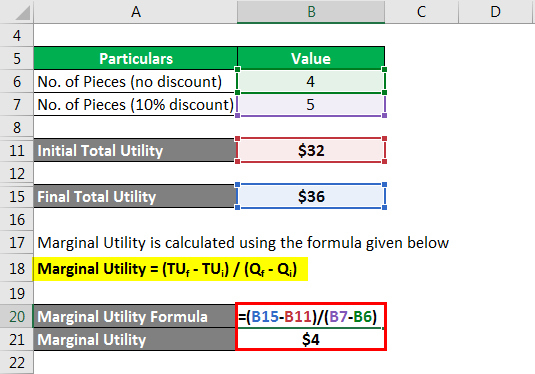
Let us take the example of David, who purchased four pastries for $8 each. Now, the bakery offers him a deal that he would be given 10% on the entire purchase if he purchases one more pastries. If David agreed to buy the additional unit, then calculate the marginal utility of the 5th piece for him.
Solution:
Initial Total Utility is calculated as
Final Total Utility is calculated as
Marginal Utility is calculated using the formula given below
Marginal Utility = (TUf – TUi) / (Qf – Qi)
- Marginal Utility = ($36 – $32) / (5 – 4)
- Marginal Utility = $4
Therefore, each piece of pastry’s marginal utility declined from $8 until the 4th piece to $4 for the 5th piece.
Explanation
The formula for Marginal Utility can be calculated by using the following steps:
Step 1: Firstly, ascertain the number of units of the good or service consumed initially and the total satisfaction (utility) gained by the consumer with that. The consumer’s willingness to pay is an indicator of the perceived value and hence can be used as a proxy for total utility. The number of units consumed initially and the total utility at that level are denoted by Qi and TUi, respectively.
Step 2: Next, ascertain the number of units consumed finally and the total utility at that level, which are denoted by Qf and TUf respectively.
Step 3: Next, determine the change in total utility by deducting the initial total utility(step 1) from the final total utility (step 2).
Change in Total Utility, ΔTU = TUf – TUi
Step 4: Next, determine the change in the number of units consumed by deducting the initial number of units consumed (step 1) from the final number of units consumed (step 2).
Change in No. of Units Consumed, ΔQ = Qf – Qi
Step 5: Finally, the formula for marginal utility can be derived by dividing the change in total utility (step 3) by the change in the number of units consumed (step 4), as shown below.
Marginal Utility = Change in Total Utility (ΔTU) / Change in No. of Units Consumed (ΔQ)
Marginal Utility = (TUf – TUi) / (Qf – Qi)
Relevance and Use of Marginal Utility Formula
Marginal utility is an important economic concept that is based on the law of diminishing marginal returns. This theory states that perceived satisfaction gained by a consumer increases with the consumption of each additional unit until a certain level, and then it starts to decrease, which indicates that the consumer is losing interest in the good or service. Now, this concept is used by sellers to understand consumer behavior and determine the price point and different levels of consumption. One of the best examples of the seller using marginal utility theory to lure consumers is at shopping malls where we come across offers on larger packs rather than the smaller ones.
Marginal Utility Formula Calculator
You can use the following Marginal Utility Formula Calculator
| Change in Total Utility (ΔTU) | |
| Change in No. of Units Consumed (ΔQ) | |
| Marginal Utility | |
| Marginal Utility | = |
|
|
Recommended Articles
This is a guide to the Marginal Utility Formula. Here we discuss how to calculate the Marginal Utility Formula along with practical examples. We also provide a Marginal Utility calculator with a downloadable excel template. You may also look at the following articles to learn more –