Updated July 25, 2023
Marginal Product Formula (Table of Contents)
What is the Marginal Product Formula?
In economics, the term “marginal product” refers to the increase in production output due to an increase in the variable input by a unit. In other words, the marginal product measures the productivity of the additional unit of the variable input.
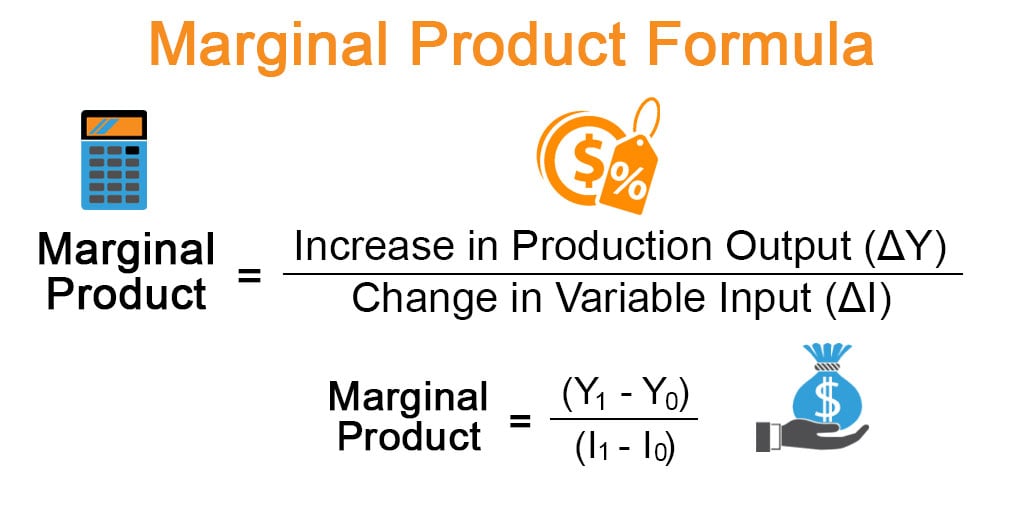
Examples of variable input can be labor, capital, etc. The formula for a marginal product can be derived by dividing the increase in production output (ΔY) by the increase in variable input (ΔI). The Mathematical representation of the formula is as below:
Further, the formula for a marginal product can be elaborated into
where,
- Y0= Initial Production Output
- Y1 = Final Production Output,
- I0 = Initial Variable Input
- I1 = Final Variable Input
Examples of Marginal Product Formula (With Excel Template)
Let’s take an example to understand the calculation of Marginal Product in a better manner.
Marginal Product Formula – Example #1
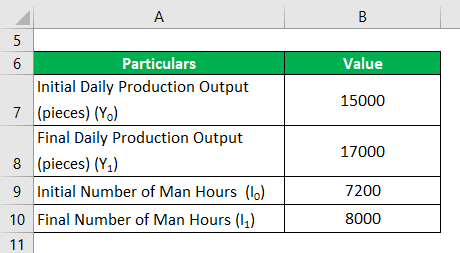
Let us take the example of a company, ERT Ltd., which is an automotive parts manufacturing company. The company’s senior management wants to study the impact of the increase in man hours on the overall production output. During a recent experiment, the daily man hours was increased from 7,200 to 8,000, increasing daily production output from 15,000 pieces to 17,000 pieces. Calculator the marginal product of one man-hour based on the given information.
Solution:
The formula to calculate Marginal Product is as below:
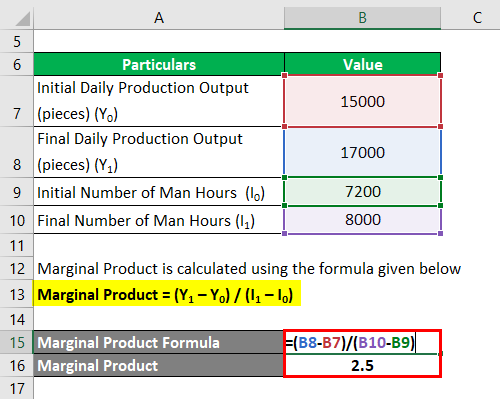
Marginal Product = (Y1 – Y0) / (I1 – I0)
- Marginal Product = (17,000 – 15,000) / (8,000 – 7,200)
- Marginal Product = 2.5 pieces per man hour
Therefore, ERT Ltd.’s marginal product is 2.5 pieces per man hour, which means adding each unit of man hour will increase the daily production output by 2.5 pieces.
Marginal Product Formula – Example #2
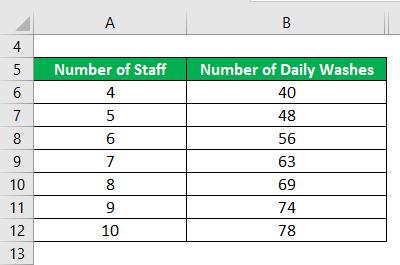
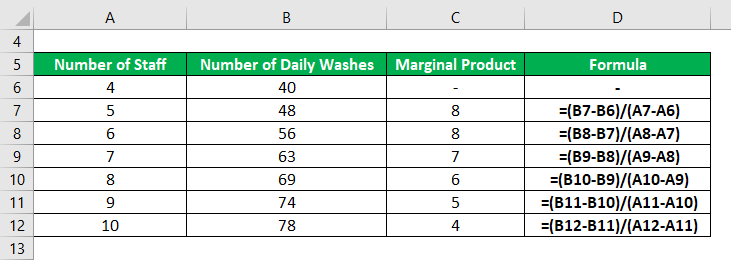
Let us take the example of a company planning to hire new staff to increase its vehicle cleaning capacity. However, the management has decided to track how each recruit adds to the daily washes performed in the company. The following shows the change in the total number of washes in a day vis-à-vis the number of employees,
Solution:
For 5th Staff Member
- Marginal Product 5th = (48 – 40) / (5 – 4)
- Marginal Product 5th = 8 daily washes
For 6th Staff Member
- Marginal Product 6th = (56 – 48) / (6 – 5)
- Marginal Product 6th = 8 daily washes
For 7th Staff Member
- Marginal Product 7th = (63 – 56) / (7 – 6)
- Marginal Product 7th = 7 daily washes
For 8th Staff Member
- Marginal Product 8th = (69 – 63) / (8 – 7)
- Marginal Product 8th = 6 daily washes
For 9th Staff Member
- Marginal Product 9th = (74 – 69) / (9 – 8)
- Marginal Product 9th = 5 daily washes
For 10th Staff Member
- Marginal Product 10th = (78 – 74) / (10 – 9)
- Marginal Product 10th = 4 daily washes
Explanation
The formula for a marginal product can be computed by using the following steps:
Step 1: Firstly, determine the production output and the variable input at the start of the period, denoted by Y0 and I0, respectively.
Step 2: Next, determine the production output and the variable input at the end of the period, denoted by Y1 and I1, respectively.
Step 3: Next, compute the increase in production output, which is the final production output (step 2) minus the initial production output (step 1).
Increase in Production Output, ΔY = Y1 – Y0
Step 4: Next, compute the increase in a variable input, the final variable input (step 2) minus the initial variable input (step 1).
Increase in Variable Input, ΔI = I1 – I0
Step 5: Finally, the formula for a marginal product can be derived by dividing the increase in production output (step 3) by the increase in variable input (step 4) as shown below.
Marginal Product = Increase in Production Output (ΔY) / Change in Variable Input (ΔI)
Marginal Product = (Y1 – Y0) / (I1 – I0)
Relevance and Use of Marginal Product Formula
It is important to understand the concept of marginal product because it is used as one of the driving factors of the level of production. The underlying theory of marginal product is the law of diminishing marginal returns, which states that marginal productivity will eventually decrease beyond a certain point owing to several operational limitations. In fact, there are cases where marginal productivity can become detrimental enough to reduce the overall production level by adding a new variable unit. In such cases, it is advisable to stop increasing that variable input.
Marginal Product Formula Calculator
You can use the following Marginal Product Formula Calculator
| Y1 | |
| Y0 | |
| I1 | |
| I0 | |
| Marginal Product | |
| Marginal Product = |
|
|
Recommended Articles
This is a guide to the Marginal Product Formula. Here we discuss how to calculate Marginal products along with practical examples. We also provide a Marginal Product calculator with a downloadable Excel template. You may also look at the following articles to learn more –