Updated March 23, 2023
Introduction to Machine Learning (ML) Lifecycle
Machine Learning Life Cycle is defined as a cyclical process which involves three-phase process (Pipeline development, Training phase, and Inference phase) acquired by the data scientist and the data engineers to develop, train and serve the models using the huge amount of data that are involved in various applications so that the organization can take advantage of artificial intelligence and machine learning algorithms to derive a practical business value.
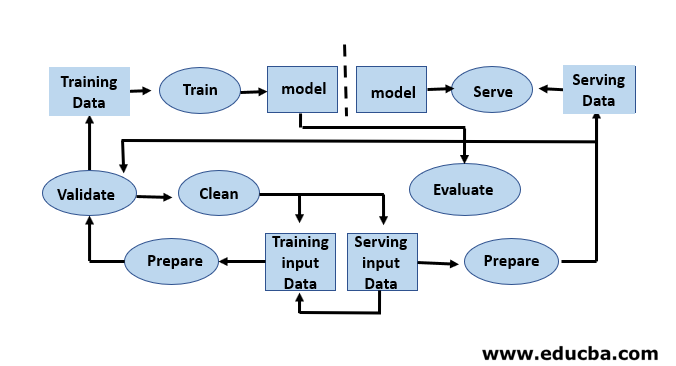
The first step in the machine learning lifecycle consists of transforming raw data into a cleaned dataset, that dataset is often shared and reused. If an analyst or a data scientist who encounter issues in the received data, they need to access the original data and transformation scripts. There are a variety of reasons that we may want to return to earlier versions of our models and data. For example, finding the earlier best version may require searching through many alternative versions as models unavoidably degrade in their predictive power. There are many reasons for this degradation, like a shift in the distribution of data that can result in a rapid decline in predictive power as compensation for errors. Diagnosing this decline may require comparing training data with live data, retraining the model, revisiting earlier design decisions or even redesigning the model.
Learning From Mistakes
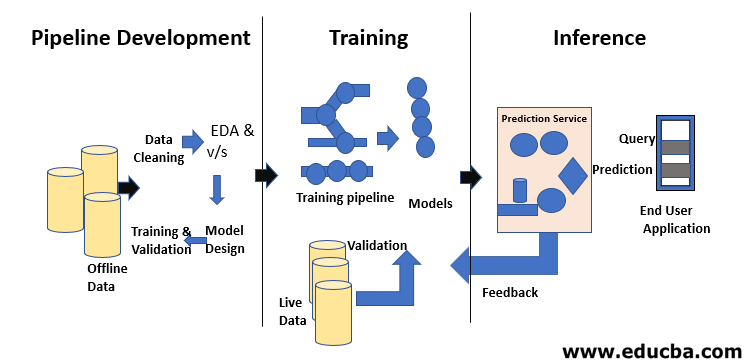
The development of models requires separate training and testing datasets. Overuse of testing data during training can lead to poor generalization and performance, as they may lead to over-fitting. Context plays a vital role here, hence it is necessary to understand which data were used to train the intended models and with which configurations. The machine learning lifecycle is data-driven because the model and the output of training is linked to the data on which it was trained. An overview of an end to end machine learning pipeline with a data point of view is shown in the figure given below:
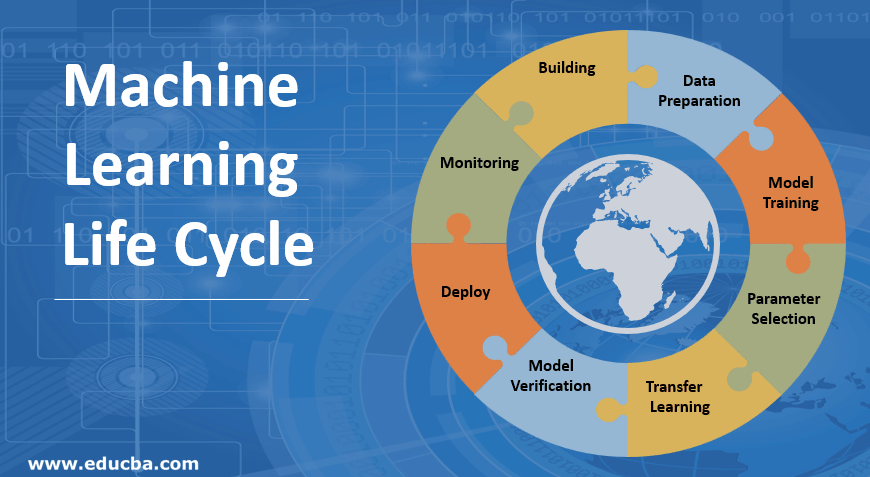
Steps Involved In Machine Learning Lifecycle
Machine Learning developer constantly performs experimentation with new datasets, models, software libraries, tuning parameters in order to optimize and enhance the model accuracy. Since the model performance depends completely on the input data and the training process.
1. Building the machine learning model
This step decides the type of the model based on the application. It also finds that the application of the model in the model learning stage so that they can be designed properly according to the need of an intended application. A variety of machine learning models are available, such as the Supervised model, Unsupervised model, classification models, regression models, clustering models, and reinforcement learning models. A close insight is depicted in the figure given below:
2. Data Preparation
A variety of data can be used as input for machine learning purposes. This data can come from a number of sources, such as a business, pharmaceutical companies, IoT devices, enterprises, banks, hospitals e.t.c. Large volumes of data are provided at the learning stage of the machine since as the number of data increases it aligns towards yielding desired results. This output data can be used for analysis or fed as input into other machine learning applications or systems for which it will act as a seed.
3. Model Training
This stage is concerned with creating a model from the data given to it. At this stage, a part of the training data is used to find model parameters such as the coefficients of a polynomial or weights of in machine learning which helps to minimize the error for the given data set. The remaining data are then used to test the model. These two steps are generally repeated a number of times in order to improve the performance of the model.
4. Parameter Selection
It involves the selection of the parameters associated with the training which are also called the hyperparameters. These parameters control the effectiveness of the training process and hence, ultimately the performance of the model depends on this. They are very much crucial for the successful production of the machine learning model.
5. Transfer Learning
Since there are a lot of benefits in reusing machine learning models across various domains. Thus, in spite of the fact that a model cannot be transferred between different domains directly, hence it is used for providing a starting material for beginning the training of a next stage model. Thus it significantly reduces the training time.
6. Model Verification
The input of this stage is the trained model produced by the model learning stage and the output is a verified model that provides sufficient information to allow users to determine whether the model is suitable for its intended application. Thus, this stage of the machine learning lifecycle is concerned with the fact that a model is working properly when treated with inputs that are unseen.
7. Deploy the machine learning model
In this stage of the Machine learning lifecycle, we apply to integrate machine learning models into processes and applications. The ultimate aim of this stage is the proper functionality of the model after deployment. The models should be deployed in such a way that they can be used for inference as well as they should be updated regularly.
8. Monitoring
It involves the inclusion of safety measures for the assurance of proper operation of the model during its life span. In order to make this happen proper management and updating are required.
Advantage of Machine Learning Life Cycle
Machine learning provides the benefits of power, speed, efficiency, and intelligence through learning without explicitly programming these into an application. It provides opportunities for improved performance, productivity, and robustness.
Conclusion
Machine learning systems are becoming more important day by day as the amount of data involved in various applications is increasing rapidly. Machine learning technology is the heart of smart devices, household appliances, and online services. The success of machine learning can be further extended to safety-critical systems, data management, High-performance computing, which holds great potential for application domains.
Recommended Articles
This is a guide to Machine Learning Life Cycle. Here we discuss the introduction, Learning From Mistakes, Steps Involved In Machine Learning Lifecycle with advantages. You can also go through our other suggested articles to learn more–