Updated July 24, 2023

Macaulay Duration Formula (Table of Contents)
What is the Macaulay Duration Formula?
Named after Frederick Macaulay, Macaulay’s Duration is the measure of the bond’s sensitivity to changes in interest rates. It is the weighted average number of days for which the investor has to hold the bond to make the present value of all the cash flows equal to the amount paid for the bond.
Macaulay duration is an important factor that investors consider before investing in any kind of debt instrument. Using the duration of the coupon payments and the inverse relationship between the interest rate and price of the bonds, investors get a sense of which bond to buy.
Mathematically, it is represented as,
Formula,
And
Where –
- T: Total Time Period
- C: Coupon Payment
- Y: Yield
- N: Total Number of Periods
- M: Maturity
- Price: Present Value of All the Cash Flows
Example of Macaulay Duration Formula (With Excel Template)
Let’s take an example to understand the calculation of the Macaulay Duration Formula in a better manner.
Macaulay Duration Formula – Example #1
Let us take the example of two bonds, A and B, with a similar face value of $100 and a frequency of 2. Bond A has a Coupon of 7%, and a Yield of 6%; on the other hand, Bond B has a Coupon of 9% and a Yield similar to the coupon at 9%. The maturity of Bond A is in 4 years, while Bond B is in 5 years. When Yield is equal to the coupon rate, face value is equal to price, like in the case of bond B, and when the coupon is greater than Yield, the price of the bond is higher than face value. In this example, we will calculate Macaulay duration using Modified Duration; this is the simplest way to calculate Macaulay duration.
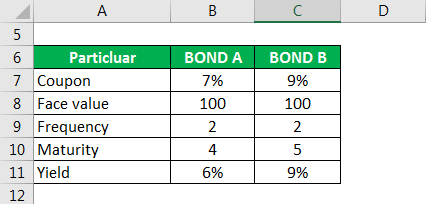
Solution:
Price is calculated as
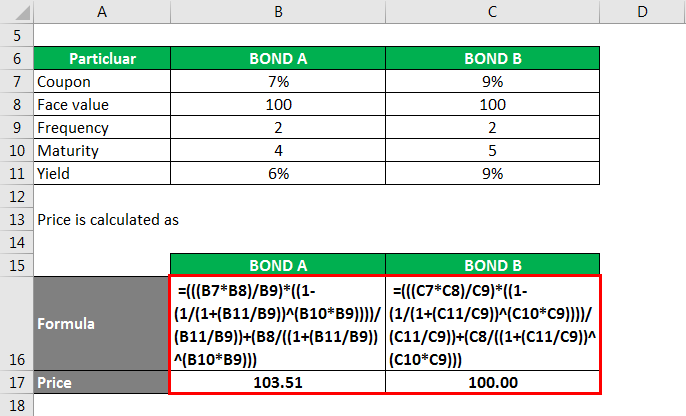
Modified Duration is calculated as
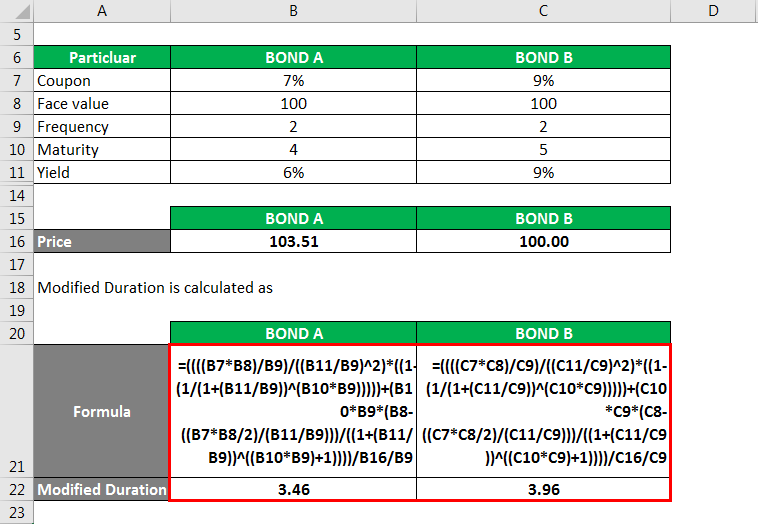
Macaulay Duration is calculated using the formula given below
Macaulay Duration = Modified Duration * (1 + (Yield/ Frequency))
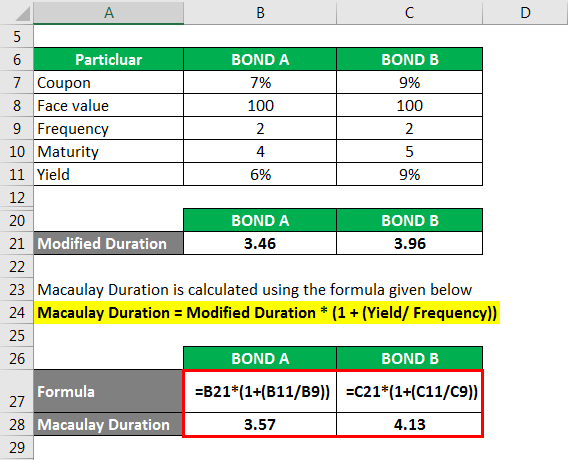
Using the above formula, Macaulay Duration of Bond A is at 3.57 while Macaulay Duration of Bond B is at 4.13.
Macaulay Duration Formula – Example #2
Let us take another example and calculate Macaulay Duration using the longer method. Let us take a Bond A $100 value bond that pays a 6% coupon rate and matures in four years. The coupon rate is 8% p.a with semi-annual payment. We can expect the following cash flows to occur: 6 months: $3, 1 year: $3, 5 years: $3, 2 years: $3, 5 years: $3, 3 years: $3, 5 years: $3, 4 years: $103. Let us now calculate Macaulay Duration using these cash flows.
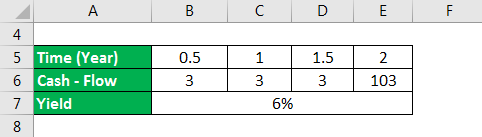
Solution:
We will first calculate the discount factors for all the periods using the formula 1 / (1+ r) n, where r is the coupon rate and n is the total number of periods for which it has to be compounded. After calculating the discount factor, we will multiply it with the cash flows to get the present value.
After calculating the discount factor, we will multiply it with the respective cash flow to get the present value and sum all the cash flows to get the bond’s Macaulay Duration.
Discount Factor is calculated as
Discount Factor for 6 months = 1 / (1 + 6%/2)
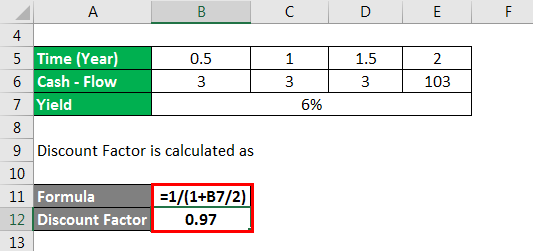
Discount factor = 0.97
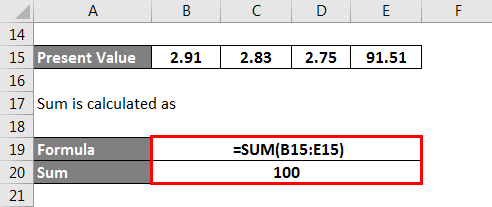
The Present Value of Cash flow is calculated as

The sum is calculated as
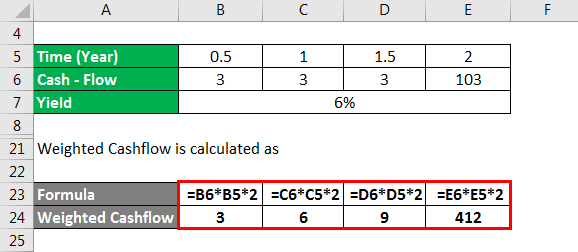
Weighted Cashflow is calculated as
Present Value of Weighted Cashflow is calculated as
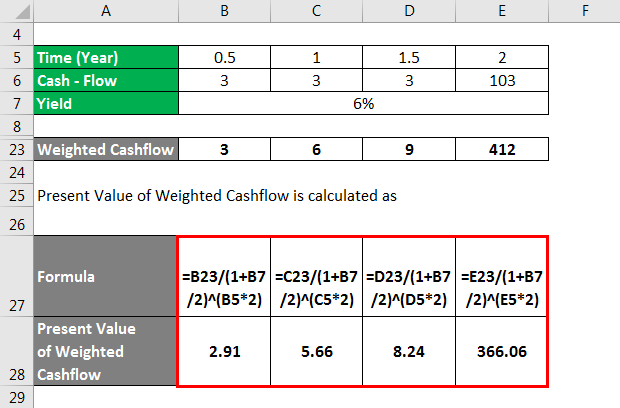
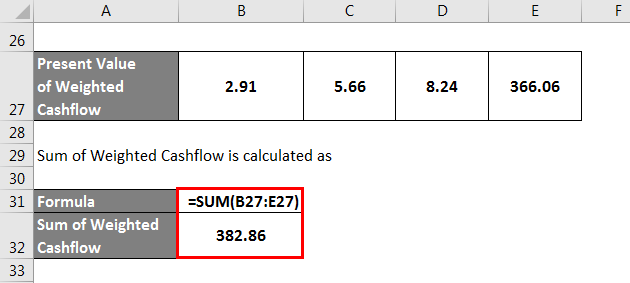
The Sum of Weighted Cashflow is calculated as
Semiannual Duration is calculated as

Macaulay Duration is calculated as

- Macaulay Duration Formula – Example #3Current Bond Price = PV of all the cash flows 382.861
- Semiannual Macaulay Duration = $ 382.861/ $100 = 3.82
- To get an annual duration simply divide the duration with two = 1.914
Macaulay Duration Formula – Example #3
One more way of calculating duration is by using an excel spreadsheet by using an inbuilt formula. The excel DURATION function calculates Macaulay Duration for a par value of $100.
Syntax: DURATION (settlement, maturity, coupon, yield, frequency, [basis] )
Where
- Settlement = Date of the Settlement of The Security
- Maturity = Maturity Date
- Coupon = Coupon Rate
- Yld = Annual Yield
- Basis = Financial Day Count Basis
- Frequency = Number of Coupon Payments Paid in A Year:
- 1: Annually
- 2: Semi-Annually
- 4: Quarterly
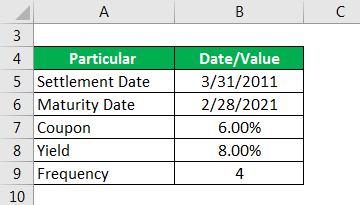
Solution:
Let us consider a $100 par bond with a Settlement date as 1st April 2015, a Maturity date as 31st March 2025, coupon rate of 6% paid quarterly with a yield of 8%
Macaulay Duration is calculated as
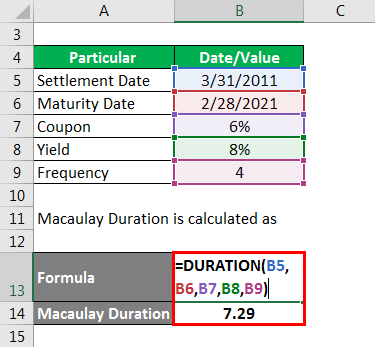
In the above calculation basis argument has been omitted in this case; the default value of 30/360-day count basis is used.
Possible Errors and their meanings in excel:
#NUM:
- It occurs if the settlement date is greater than or equal to the maturity date
- If the numbers are invalid for either Coupon, yield, and frequency
#VALUE:L
- Any values are not numeric.
- Or any one of the dates or both are not excel valid dates
Explanation
The Macaulay Duration Formula can be calculated by using the below explanation:
Macaulay Duration considers the time, coupon payment, the current yield, par value of the bond and the price to arrive at a number. All this information can be accessed easily, and using the above formula; Duration can be calculated.
Relevance and Use of Macaulay Duration Formula
Understanding duration helps an investor in determining the correct pick of fixed income security. Just as mean, standard deviation, beta act as a measure for equities, Macaulay Duration is for fixed income securities. One important point to consider is that Duration is a good approximation for an option free bond with small changes in interest rates. When rates increase and become larger, it becomes increasingly important to understand the bond yield relationship; however, using a linear approximation like duration will contain a lot of errors.
Recommended Articles
This is a guide to the Macaulay Duration Formula. Here we discuss how to calculate the Macaulay Duration Formula along with practical examples. We also provide a downloadable excel template. You may also look at the following articles to learn more –

