Introduction to Jump Search Algorithm
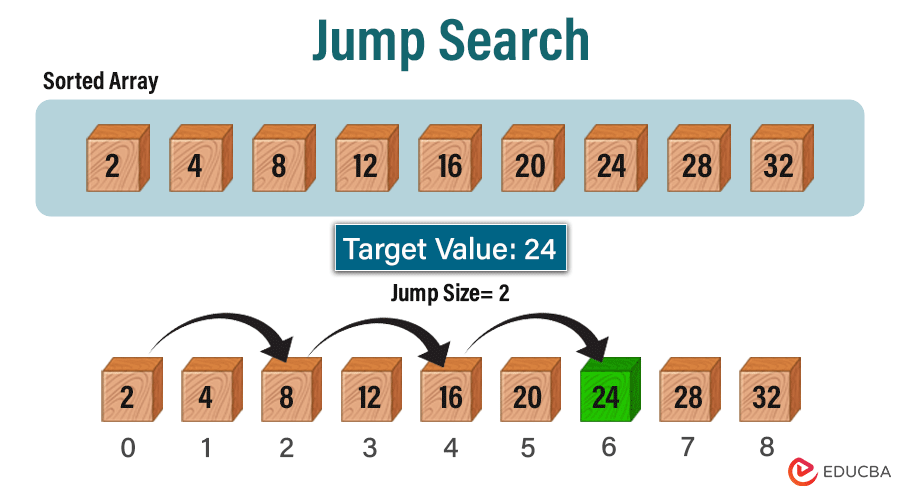
Jump Search, an algorithm designed to locate a target value within a sorted array, represents a significant improvement over linear search, particularly for large datasets. Instead of sequentially traversing the entire array, Jump Search jumps ahead by fixed intervals. It divides the array into smaller blocks or subarrays and systematically jumps from one block to another, significantly reducing the number of comparisons required. For Jump Search, sorting the array is a crucial prerequisite. Once it identifies a potential block containing the target value, the algorithm performs a linear search to pinpoint the target’s position precisely. Although Jump Search doesn’t promise the logarithmic time complexity of binary search, its balanced approach between simplicity and efficiency often outperforms linear search, especially for sizable datasets. This algorithm’s strategic jumping mechanism makes it well-suited for efficiently handling large datasets by minimizing the number of comparisons necessary.
Table of Contents
How Jump Search Works
It functions by segmenting the sorted array into blocks or subarrays of consistent size and then employing a blend of jumping and linear search methods to locate the desired value. Here’s a detailed breakdown of its operation:
- Determining Jump Size: Initially, the algorithm calculates the jump size, often based on the square root of the array’s length or other criteria geared towards optimizing search efficiency.
- Navigating Through Blocks: Jump Search proceeds by leaping forward in fixed intervals within the array, comparing the target value with the elements at these predetermined jump points.
- Locating the Relevant Block: Once a leap surpasses the target value, the algorithm, guided by the comparison outcomes, identifies the block where the target value is likely situated.
- Conducting Linear Search Within the Block: Inside the identified block, Jump Search executes a linear search to pinpoint the target value’s location precisely.
- Returning the Outcome: Should the target value be discovered during the linear search within the block, Jump Search returns the index of the target element. Otherwise, it signifies that the target value is absent from the array.
Implementation
Consider an array of integers stored in sorted order.
We want to find the index of the target value 23 using Jump Search.
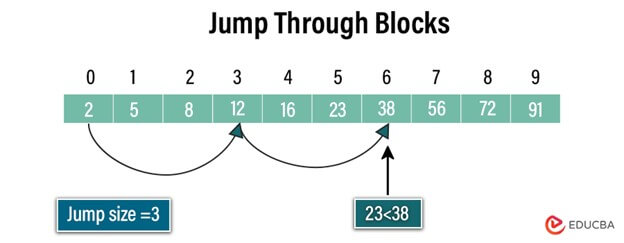
Step 1: Determine Jump Size
Let’s consider using the square root of the array’s length to determine the jump size. For instance, with an array length of 10, the jump size would be approximately 3, rounded to the nearest integer.
Step 2: Jump Through Blocks
Begin traversing the array by jumping at intervals determined by the jump size. Compare the target value with the element at the current index until either the value at the current index exceeds the target value or the end of the array is reached.
Step 3: Identify the Block Containing the Target
Once the value at the current index exceeds the target value, identify the block where the target value is likely to be present based on the previous jump.
Step 4: Perform the Linear Search Within the Block
Perform a linear search within the identified block to locate the target value precisely. Return the target value index if the block’s linear search finds it. Otherwise, indicate that the target value is not present in the array.
Pseudocode
function jumpSearch(array, target):
n = length of array
jump_size = floor(sqrt(n))
prev = 0
current = jump_size
// Jump through blocks until the target value is exceeded
while array[min(current, n) - 1] < target: prev = current current += jump_size if prev >= n:
return -1 // Target is not present in the array
// Perform linear search within the identified block
for i from prev to min(current, n):
if array[i] == target:
return i // Target found at index i
return -1 // Target is not present in the arrayExplanation:
- Function Declaration: Defines a function named jumpSearch that accepts an array and a target value as arguments, returning the index of the target value if found or -1 if not present.
- Initialization: Initializes variables n to the length of the array, jump_size to the square root of n, prev to 0, and current to jump_size.
- Jump Through Blocks: Using a while loop, it jumps through blocks until the target value is exceeded or the end of the array is reached.
- Linear Search Within Block: Within a for loop, it performs a linear search within the identified block.
- Return Outcome: Returns the index of the target value if found or -1 if not present.
Complexity Analysis
Jump Search has a time complexity of O(√n), where ‘n’ stands for the number of elements present in the array. This complexity stems from jumping through the array in fixed-size blocks and conducting a linear search within the identified block. Regarding space complexity, Jump Search requires O(1) space since it utilizes only a constant amount of additional memory for variables.
Examples
Example 1: Lower Time Complexity
Code
import math
def jump_search(arr, target):
n = len(arr)
jump_size = int(math.sqrt(n))
prev = 0
current = jump_size
# Jump through blocks until the target value is exceeded
while arr[min(current, n) - 1] < target: prev = current current += jump_size if prev >= n:
return -1 # Target is not present in the array
# Perform linear search within the identified block
for i in range(prev, min(current, n)):
if arr[i] == target:
return i # Target found at index i
return -1 # Target is not present in the array
# Lower Time Complexity
arr1 = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
target1 = 13
result1 = jump_search(arr1, target1)
print("Example 1: Lower Time Complexity")
if result1 != -1:
print(f"Target {target1} found at index {result1}")
else:
print(f"Target {target1} not found in the array")Output:
Example 2: Higher Time Complexity
Code:
import math
def jump_search(arr, target):
n = len(arr)
jump_size = int(math.sqrt(n))
prev = 0
current = jump_size
# Jump through blocks until the target value is exceeded
while arr[min(current, n) - 1] < target: prev = current current += jump_size if prev >= n:
return -1 # Target is not present in the array
# Perform linear search within the identified block
for i in range(prev, min(current, n)):
if arr[i] == target:
return i # Target found at index i
return -1 # Target is not present in the array
# Higher Time Complexity
arr2 = [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
target2 = 25
result2 = jump_search(arr2, target2)
print("\nExample 2: Higher Time Complexity")
if result2 != -1:
print(f"Target {target2} found at index {result2}")
else:
print(f"Target {target2} not found in the array")Output:
Pros and Cons of Jump Search
Advantages:
- Efficiency for Large Datasets: It is particularly efficient for searching large datasets. Dividing the array into smaller blocks and jumping through them significantly reduces the number of comparisons required compared to linear search, resulting in faster search times.
- Balanced Approach: It strikes a balance between simplicity and efficiency. While it may not offer the logarithmic time complexity of binary search, it often outperforms linear search, especially for moderately sized datasets, making it a practical choice in various scenarios.
- Ease of Implementation: It is relatively easy to implement. Unlike binary search, which requires sorting the array and involves complex partitioning steps, Jump Search only necessitates sorting the array, and its straightforward jumping mechanism makes it accessible to implement.
- Suitable for Linked Lists: It can be adapted for linked lists with minor modifications. While binary search is unsuitable for linked lists due to the lack of random access, Jump Search’s block-based approach allows it to navigate linked lists efficiently.
Disadvantages:
- Sorted Array Prerequisite: It mandates arranging the array in ascending order. This prerequisite ensures the algorithm’s accuracy, albeit it might pose a challenge if the variety isn’t pre-sorted or sorting it isn’t feasible due to time or space constraints.
- Not Universally Optimal: Despite Jump Search’s efficiency advantages over linear search, it might not always be the optimal solution. More advanced search techniques like binary or interpolation search could yield superior performance, particularly for expansive datasets with irregular distributions.
- Moderate Efficiency Enhancements: Unlike binary search, which boasts logarithmic time complexity, Jump Search operates at O(√n) time complexity, where n represents the array’s size. Although it outperforms linear search, its efficiency might not match that of binary search for massive datasets.
Real-World Applications
- Database Management Systems: It is valuable for efficiently navigating sorted datasets in database management systems. Its application facilitates the swift retrieval of specific records within sorted databases, enhancing information retrieval processes.
- File Management Systems: Within file systems, where files often organize themselves in a sorted fashion based on attributes like file names or creation dates, Jump Search emerges as a tool for expedited file location. Leveraging Jump Search optimizes file retrieval operations, contributing to improved system performance.
- Text Editing and Word Processing: Text editors and word processors routinely employ sorted indexes for words or phrases within documents. By incorporating Jump Search, these applications streamline locating and editing specific content within documents, fostering efficient text manipulation.
- Web Search Engines: Web search engines meticulously index web pages using keywords and other criteria. Integrating Jump Search into their indexing and retrieval mechanisms enables rapid identification of relevant web pages in response to user queries, thereby enhancing search engine efficiency.
- Scientific and Engineering Applications: In scientific and engineering domains, Jump Search finds utility in sifting through sorted numerical datasets. Its implementation facilitates the precise location of specific data points or patterns within extensive datasets, supporting various data analysis and visualization tasks.
- Network Routing Systems: In such cases, files often organize themselves in a sorted fashion based on attributes like file names or creation dates. Integrating Jump Search into network routers facilitates swift and efficient navigation of routing tables, aiding in determining the optimal next hop for packet forwarding.
- Genetic Research: Genetic sequencing databases categorize genetic information based on genetic markers in sorted order. Leveraging Jump Search in genetic research enables the swift identification of specific genetic sequences or patterns within these databases, thereby supporting gene discovery and analysis endeavors.
- Digital Libraries: Digital libraries meticulously organize digital resources such as books, articles, and multimedia files based on metadata attributes. By incorporating Jump Search, digital libraries expedite locating resources in response to user queries, enriching user experience and facilitating seamless information access.
Conclusion
Jump Search is a pragmatic solution for efficiently searching sorted datasets in various real-world scenarios. Its balanced approach, striking a chord between simplicity and efficiency, makes it particularly well-suited for moderately sized datasets where the overhead of more complex algorithms may not justify their use. While it may not offer the logarithmic time complexity of binary search, its systematic jumping mechanism significantly reduces the number of comparisons required compared to linear search, thus offering a notable improvement in search efficiency. It is a valuable tool for enhancing search operations and optimizing performance in diverse domains when applied judiciously in appropriate contexts.
Frequently Asked Questions (FAQs)
Q1. Is the Jump Search algorithm suitable for all types of datasets?
Answer: It is most effective for moderately sized datasets, whereas more complex algorithms like binary search may not justify their use due to their overhead. Other search algorithms may perform better for massive datasets or irregular distributions.
Q2. Can Jump Search be used to search in linked lists?
Answer: We can adjust Jump Search to search in linked lists with slight modifications. Unlike binary search, which is unsuitable for linked lists due to random access, Jump Search’s block-based method enables it to traverse linked lists efficiently.
Q3. Does Jump Search outperform binary search for all datasets?
Answer: Jump Search proves most effective for moderately sized datasets, finding a harmonious equilibrium between simplicity and efficiency. Nevertheless, in instances involving massive datasets or those with irregular distributions, a binary search may excel due to its logarithmic time complexity, offering superior performance.
Recommended Articles
We hope that this EDUCBA information on “Jump Search” was beneficial to you. For more information, you can view EDUCBA’s recommended articles.