Updated March 4, 2023
Definition of Heap Data Structure
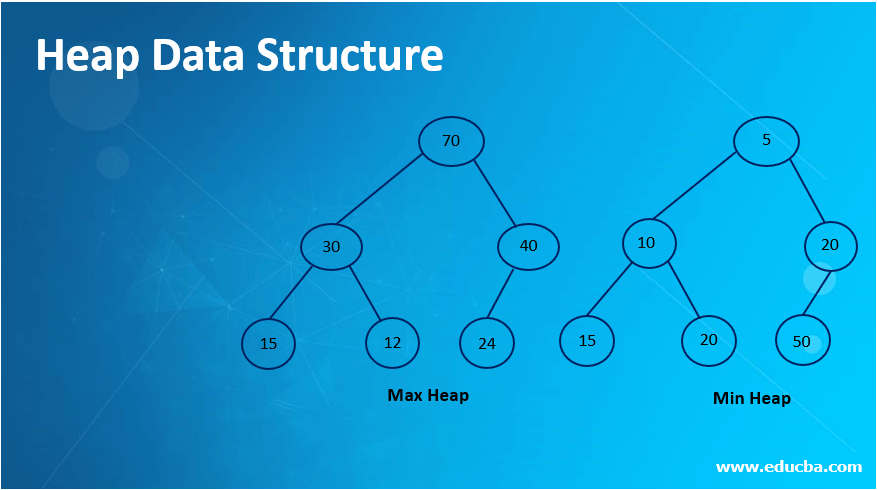
A heap is a special type of tree that satisfies certain conditions such as it is a complete binary tree and the value in the parent node in a heap is always either greater than or equal to the value in its child nodes in case of max heap or value in parent node is smaller than the value stored in its child node. This type of data structure has been constructed to implement scenarios such as priority queues where one needs to pick the element with least or highest priority. Also the tree in a heap is always balanced.
Heap Data Structure Types
Types of Heap Data Structure are:
1. Max Heap
This is a type of heap where the value in the root element is greater or equal to the elements present in its child node.
Algorithm
- Step 1: First create a new node N at the end of the heap.
- Step 2: The new element to be added will be assigned to this node N
- Step 3: Repeat Step 3 and 4 until node reaches its correct position.
- Step 3:Values of this node N is compared to parent of N.
- Step 4:If value of parent[N] < any of its child then swap them
Working
Max heap is a complete binary tree that stores the elements in its node following one cireteriai.e Parent[N] is greater than or equal to its child node. The elements of max heap are mapped into an array my_arr following below criteria –
- Root of the heap is stored at first location of array my_arr.
- In case an element is stored at m location in the array then its left child is stored at 2*m+1 location.
- And right child of the node is stored at 2*m +2 location.
- Also root of the element is greater or equal to its child node.
This way a max- heap can be mapped to an array in the memory and can be retrieved easily using these guidelines. Various operations such as insertion, deletion, accessing can be performed on max heap .
It helps in the applications where one needs to sort the elements in decreasing order as the highest element in the heap is present at the root and can be removed one by one and build heap on remaining elements in the heap again. It is also efficient and enhances the performance of the program and memory.
Example
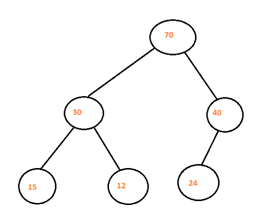
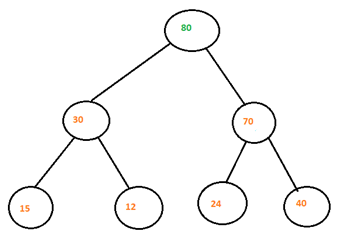
Lets explore one example for the above-given max- heap where we add a new element with value =80 to the heap.
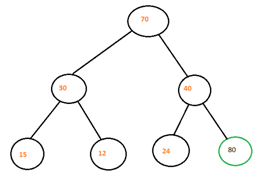
Step 1: First we add a new node with value =80 to the last of the heap that is right child of the node 40. In case node 24 was not there we will insert node 80 as the left child of the heap.
Step 2: Now we will compare new node 80 with its parent node i.e 40. Since 80> 40 then we will swap the nodes. Now 80 becomes parent of 40.
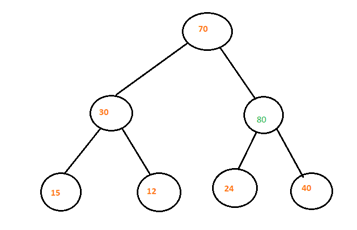
Step 3: Now we will compare node 70 and 80 and Since 80 > 70 thus we will swap those nodes. And now we will see 80 is in its correct position thus max heap has been built successfully.
2. Min Heap
This is a type of heap where the value of elements stored in the root node is lesser or equal to the value of elements stored in its child node.
Algorithm
- Step 1: First create a new node N at the end of the heap.
- Step 2: The new element to be added will be assigned to this node N
- Step 3: Repeat Step 3 and 4 until node reaches its correct position.
- Step 3: Values of this node N is compared to parent of N.
- Step 4: If value of parent[N] > any of its child then swap them.
Working
Min heap is a complete binary tree that stores the elements in its node following one cireteriai.e Parent[N] is lesser than or equal to its child node. The elements of max heap are mapped into an array my_arr following below criteria –
- Root of the heap is stored at first location of array my_arr.
- In case an element is stored at m location in the array then its left child is stored at 2*m+1 location.
- And right child of the node is stored at 2*m +2 location.
- Also root of the element is lesser than or equal to its child node.
This way a max- heap can be mapped to an array in the memory and can be retrieved easily using these guidelines. Various operations such as insertion ,deletion, accessing can be performed on min heap .
It helps in the applications where one needs to sort the elements in increasingorder such as priority queues as the smallest element in the heap is present at the root and can be removed one by one and build heap on remaining elements in the heap again. It is also efficient and enhances the performance of the program and memory.
Example
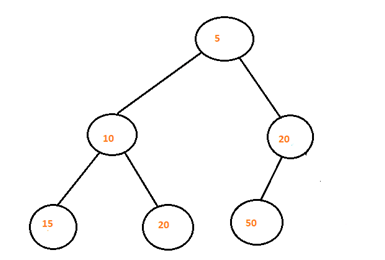
In this example we will build a min heap when a new node with value 5 is inserted in the above given heap.
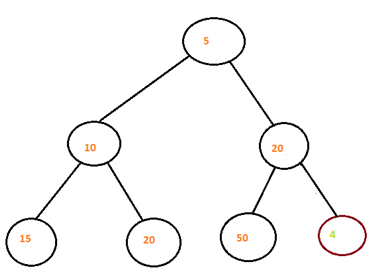
Step 1: First we will insert the new node with value 4 at the end of the heap . And see if it is its correct position. As we can see parent of new node is 20 and 4> 20 thus we need to swap the two node acccoding to step 4 in the algorithm.
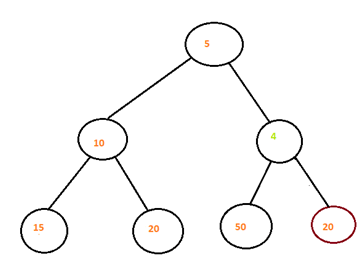
Step 2: Now node 4 has been swapped to new position. Now we will compare node 4 and its parent node 5 and we see that 5 > 4 and thus needs to be swapped again.
Step 3: Now new node 4 is at the root of the min heap . Now we observe node 4 is at its right position thus new node 4 has been inserted successfully and new min heap has been built.
3. Binary Heap
This is a type of binary heap is a binary tree that satisfies all the properties of complete binary tree. Further binary heap can be represented using above 2
Conclusion
Heap data structure is a special type of balanced complete binary tree that exist either as max –heap where value of the parent node is always greater than or equal to value in the child node or as min-heap where value of the parent node is smaller or equal to the values in its child node.
Recommended Articles
This is a guide to Heap Data Structure. Here we also discuss the definition and types of heap data structure along with an explanation. You may also have a look at the following articles to learn more –