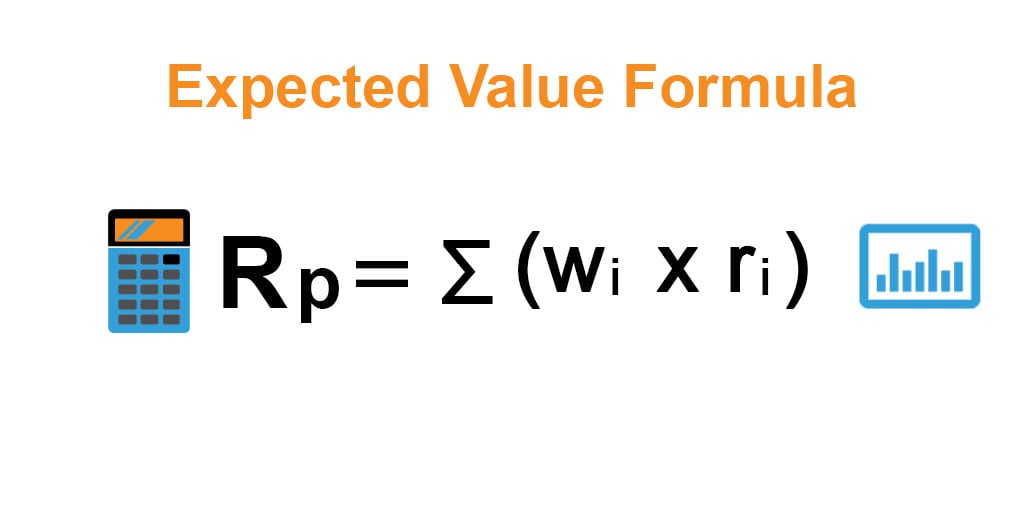Updated February 7, 2023
Expected Value Formula (Table of Contents)
What is the Expected Value Formula?
Expected Value is the expected outcome of a certain investment, which is calculated based on the weighted average of all possible values of a random variable defined based on their specific probabilities.
Portfolio managers may have several assets in their portfolios in different proportion. No the challenge for him, how to calculate the overall return from the entire portfolio of assets. However, which is calculated based on the weighted average returns of all the assets compile into the portfolio.
And some of the basics which will help you out to calculate further the expected value, variance & standard deviation of any specific portfolio.
The Expected return or value of a portfolio is presented as such.
Where,
∑ wi= 1
- w = Weights of each asset
- r = Returns on the assets
Suppose an asset of a portfolio constitutes 25% of the overall portfolio then it would consider that the weight will be 0.25 of that asset. The composite weight of all the assets in the portfolio is 1, which is considered it to be a 100% investment.
Examples of Expected Value Formula (With Excel Template)
Let’s take an example to understand the calculation of Expected Value in a better manner.
Expected Value Formula – Example #1
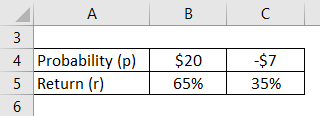
If there is a probability of gaining $20 at 65% and of losing $7 at the rate of 35%. Calculate the expected value.
Solution:
Expected Value is calculated using the formula given below
Expected Value = ∑ (pi * ri)
- Expected Value = ($20 * 65%) + ((-$7) * 35%)
- Expected Value = $10.55
Therefore, the expected value of the given estimated probabilities is such as $10.55.
Expected Value Formula – Example #2
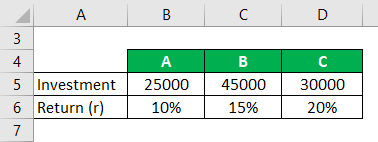
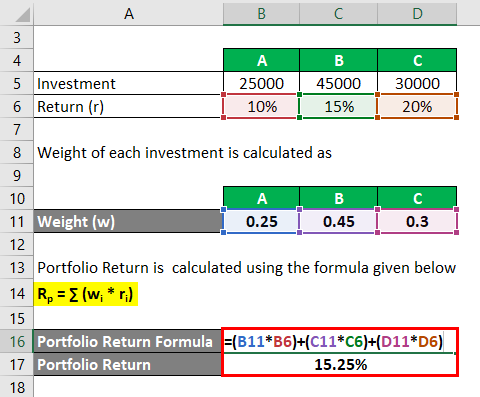
If we consider three asset A, B, C of the portfolio where we need to calculate the overall return of the portfolio.
Solution:
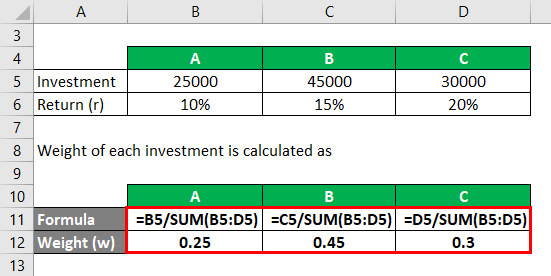
Weight of each investment is calculated as
- WA = 25000 / 100000 = 0.25
- WB = 45000 / 100000 = 0.45
- WC = 30000 / 100000 = 0.30
Portfolio Return is calculated using the formula given below
Rp = ∑ (wi * ri)
- Portfolio Return = (0.25 * 10%) + (0.45 * 15%) + (0.30 * 20%)
- Portfolio Return = 15.25%
Expected Value Formula – Example #3
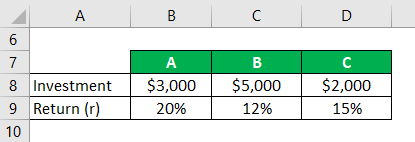
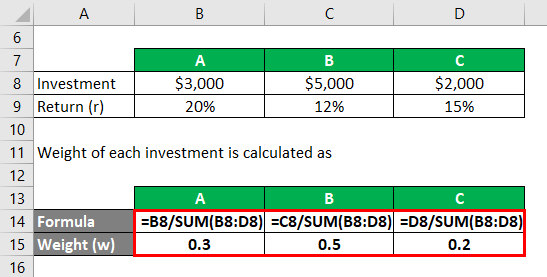
Let’s take an example where a portfolio comprises investments in three assets A, B and C and their investment in every asset is like $3,000 is invested in A, $5,000 invested in B, and $2,000 is invested in C. Now assume that the expected return which we are obtaining for each of the investments A, B, C is 20%, 12%, and 15% respectively. So on the basis of the respective investments of $3,000, $5,000 and $2,000 in each of the asset of the portfolio. Calculate the Expected Return of portfolio.
Solution:
Weight of each investment is calculated as
- WA = $3000 / $10000 = 0.3
- WB = $5000 / $10000 = 0.5
- WC = $2000 / $10000 = 0.2
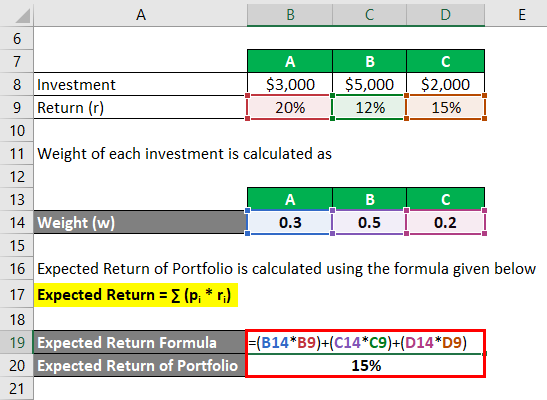
Expected Return of Portfolio is calculated using the formula given below
Expected Return = ∑ (pi * ri)
- Expected Return of Portfolio = (0.3 * 20%) + (0.5 * 12%) + (0.2 * 15%)
- Expected Return of Portfolio = 15%
The overall return of the portfolio is 15%.
Apart from calculating the expecting return, the investor is also interested in determining the risk associated with each of the investment assets before investing in a specific asset. To determine whether the portfolio’s components are properly aligned to meet the investor’s risk tolerance and investment goals.
If we take an example, where each of the assets of two different portfolios shows the following returns, respectively five years:
Portfolio Component A: 12%,8%,20%,-10%,15%
Portfolio Component B: 7%,9%,6%,8%,15%
If we calculate the expected return for both portfolio components yields the same expected return of 9%. Whereas, each component is scrutinized the risk involved in it, based on the yearly deviation from the average expected return. And you would also realize components of Portfolio A contains 5 times more risk than the portfolio component B. Standard deviation states the level of variance from the average value.
Explanation
How to Calculate the Expected Return of Investment?
The formula for different probable returns through which we calculate the expected return for an investment which is calculated in the following steps:
Step 1: Initially, we need to determine how much we are going to invest and worth of the investment at the beginning of the investment.
Step 2: Then find out the worth of the investment at the end of the period.
Step 3: Now, calculate the return based on the asset value at each probability at every initial phase and end of the period.
Step 4: Finally, the expected return of an investment which we obtain at different probable returns is the sum of the product of each probable return and the corresponding probability of a given asset.
Expected Return = ∑ (pi * ri)
Where,
- p= Probability of a specific asset
- r = Return of the corresponding asset
How to Calculate the Expected Return of the Portfolio?
The various steps by which we can calculate the expected return of portfolio which is an extension of the expected return of investment, here we give more emphasis on the weighted average of returns of each investment in the portfolio and it is calculated as follows:
Step 1: Initially, we need to determine an amount which we are going to invest at the start of the period.
Step 2: In the next step, we need to determine the weight of each asset form the portfolio which is denoted as w.
Step 3: Finally, the expected return of a portfolio with varying returns is calculated as a sum of the product of varying returns of each of the asset form the portfolio along with their respective weight as specified below:
Expected Return = ∑ (wi * ri)
Where
- w = Weight of a specific asset
- r = Return of the corresponding asset
Relevance and Uses of Expected Value Formula
Expected return plays a vital role in determining the overall return of the portfolio, it is widely used by the investors to anticipate the profit or loss may have while investing in it. Based on the expected return formula an investor can decide whether he should continue to remain invested in the given probable returns. Moreover, an investor can also give more emphasis on the weight of an asset whether any sort of tweaking is required.
Apart from that investor can also use the expected return formula for ranking purposes and further can decide on the basis ranking whether they need to keep investing in the same asset. More the expected return of an asset better is the asset.
Expected Value Formula Calculator
You can use the following Expected Value Calculator
| w1 | |
| r1 | |
| w2 | |
| r2 | |
| Rp | |
| Rp = | (w1 x r1) + (w2 x r2) |
| = | (0 x 0) + (0 x 0) = 0 |
Recommended Articles
This is a guide to the Expected Value Formula. Here we discuss How to Calculate Expected Value along with practical examples. We also provide an Expected Value Calculator with a downloadable excel template. You may also look at the following articles to learn more –