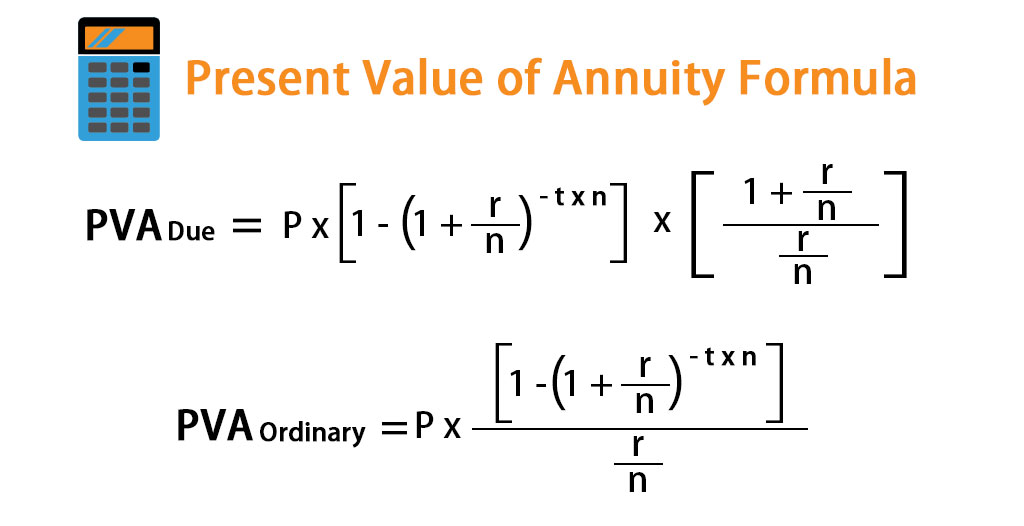Updated July 26, 2023
Present Value of Annuity Formula (Table of Contents)
What is Present Value of Annuity Formula?
The term “present value of annuity” refers to the series of equal future payments that are discounted to the present day. However, the payment can be received either at the beginning or at the end of each period and accordingly there are two different formulations.
In case the cash flow is to be received at the beginning, then it is known as the present value of an annuity due and the formula can be derived based on the periodic payment, interest rate, number of years and frequency of occurrence in a year. Mathematically, it is represented as,
where,
- PVA = Present Value of Annuity
- P = Periodic Payment
- r = Interest Rate
- t = Number of Years
- n = Frequency of Occurrence in a year
In case the cash flow is to be received at the end of each period, then it is known as the present value of the ordinary annuity and the formula is slightly different and it is expressed as,
Examples of Present Value of Annuity Formula (With Excel Template)
Let’s take an example to understand the calculation of Present Value of Annuity in a better manner.
Present Value of Annuity Formula – Example #1
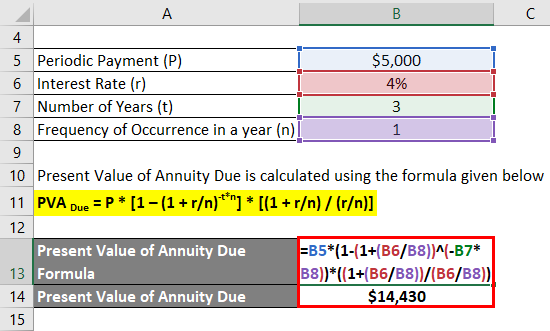
Let us take the example of an annuity of $5,000 which is expected to be received annually for the next three years. Calculate the present value of the annuity if the discount rate is 4% while the payment is received at the beginning of each year.
Solution:
Present Value of Annuity Due is calculated using the formula given below
PVA Due = P * [1 – (1 + r/n)-t*n] * [(1 + r/n) / (r/n)]
- Present Value of Annuity Due = $5,000 * [1 – (1 + (4%/1))-3*1] * [(1 + (4%/1)) / (4%/1)]
- Present Value of Annuity Due =$14,430
Therefore, the present value of the annuity is $14,430.
Present Value of Annuity Formula – Example #2
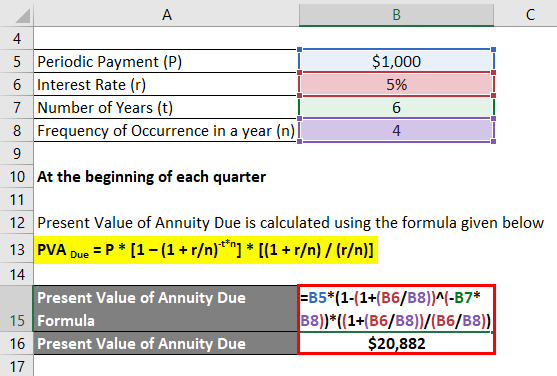
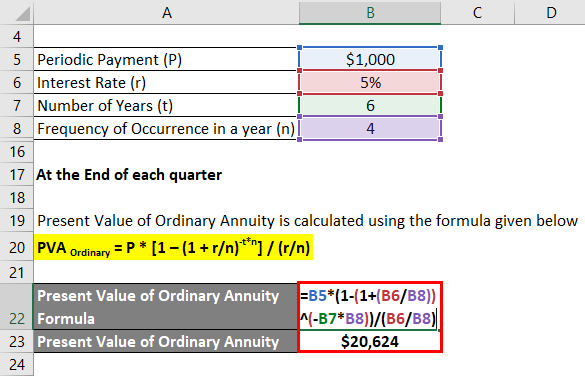
Let us take the example of David who is expected to receive a series of equal quarterly future cash inflow of $1,000 for the next six years. Calculate the present value of the future cash inflow if the relevant discounting rate based on the ongoing market rate is 5% while the payment is received:
- At the beginning of each quarter
- At the End of each quarter
Solution:
At the beginning of each quarter
Present Value of Annuity Due is calculated using the formula given below
PVA Due = P * [1 – (1 + r/n)-t*n] * [(1 + r/n) / (r/n)]
- Present Value of Annuity Due = $1,000 * [1 – (1 + (5%/4))-6*4] * ((1 + (5%/4)) / (5%/4))
- Present Value of Annuity Due = $20,882
At the End of each quarter
Present Value of Ordinary Annuity is calculated using the formula given below
PVA Ordinary = P * [1 – (1 + r/n)-t*n] / (r/n)
- Present Value of Ordinary Annuity = $1,000 * [1 – (1 + 5%/4)-6*4] / (5%/4)
- Present Value of Ordinary Annuity = $20,624
Therefore, the present value of the cash inflow to be received by David is $20,882 and $20,624 in case the payments are received at the start or at the end of each quarter respectively.
Explanation
Let us first look at the formula for the present value of an annuity due and then the one for the present value of the ordinary annuity and each of them can be derived by using the following steps:
Step 1: Firstly, figure out the equal periodic payment which is expected to be made either at the beginning or end of each period. It is denoted by P.
Step 2: Next, figure out the interest rate on the basis of the ongoing market rates and it will be used to discount each periodic payment to the present day. It is denoted by r.
Step 3: Next, figure out the number of years for which the future payments are expected to be received and it is denoted by t.
Step 4: Next, determine the frequency or occurrence of the payments in a year and it is denoted by n. It can be used to calculate the effective rate of interest and number of periods as shown below.
Effective Interest Rate = r / n
Number of Periods = t* n
Step 5: In case the cash flow is to be received at the beginning of each period, then the formula for present value of annuity due can be derived on the basis of periodic payment (step 1), effective interest rate (step 4) and number of periods (step 4) as shown below.
PVA Due = P * [1 – (1 + r/n)-t*n] * (1 + r/n) / (r/n)
On the other hand, if the cash flow is to be received at the end of each period, then the formula for the present value of an ordinary annuity can be expressed as shown below.
PVA Ordinary = P * [1 – (1 + r/n)-t*n] / (r/n)
Relevance and Uses of Present Value of Annuity Formula
Although the concept of the present value of an annuity is simply another expression of the theory of time value of money, it is an important concept from the perspective of valuation of retirement planning. In fact, it is predominantly used by accountants, actuaries and insurance personnel to calculate the present value of structured future cash flows. It is also useful in the decision – whether a lump sum payment is better than a series of future payments based on the discount rate. Further, the above-mentioned decision is also influenced by the fact that whether the payment is received at the beginning or at the end of each period.
Present Value of Annuity Formula Calculator
You can use the following Present Value of Annuity Calculator
| P | |
| r | |
| t | |
| n | |
| PVA | |
| PVA = | P x [1 -(1 +r/ n)-txn] X [1 +r / n / r / n] |
| = | 0 x [1 -(1 +0/ 0)-0x0] X [1 +0 / 0 / 0 / 0] = 0 |
Recommended Articles
This has been a guide to Present Value of Annuity Formula. Here we discuss how to calculate Present Value of Annuity along with practical examples. We also provide Present Value of Annuity calculator with downloadable excel template. You may also look at the following articles to learn more –