Updated July 27, 2023
Definition of Derivatives Example
The following derivative example provides an overview of the most prevalent derivative instruments.
A derivative is a financial security whose value is derived from an underlying asset. Underlying assets can be equity, index, foreign exchange, commodity, or other assets.
So from the above definition, it is clear that derivative products do not have their own value; any particular underlying assets decide their value. The main participant in derivative markets are hedgers, speculators, and arbitragers. Below are examples of a derivative that illustrate the most common derivatives. It is impossible to provide all types of derivative examples since thousands of such derivatives vary in every situation.
Examples of Derivatives (With Excel Template)
Let’s try to understand derivatives through the below examples.
#1 Derivatives Example – Futures Contract
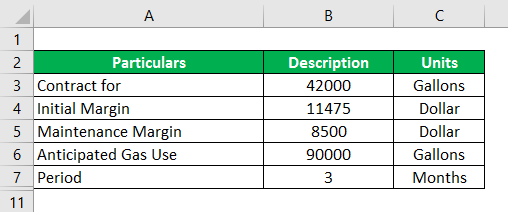
ABC Co. is a delivery company whose expenses are tied to fuel prices. ABC Co. anticipated that they use 90,000 gallons of gasoline per month. It is July 1st, and the company wants to hedge its next 3 months of fuel costs using the RBOB Gasoline future contracts. Information on these contracts is as follows.
- Each contract is for 42,000 gallons.
- Contracts expire at the end of the prior month. For example, if we have to buy the August contract that will expire at the end of July.
- The initial margin is $11,475, and the maintenance margin is $8,500.
Given,
Question-1 – Should ABC Co. Buy (Long) or Sell (Short) the Future to Initiate its Position?
Solution:
ABC Co.’s exposure is to the gas price; if the gas price goes up, its expenses will go up, and due to expenses, profit will go down. So if an ABC Co wants to hedge that risk exposure and protect its profit, they need a situation where the future position will increase in value when gas prices go up. So if a company goes for a long contract, buy gasoline futures so that the company will profit when gas goes up, which will offset natural risk exposure. So the ABC Co. hedge position is to go long (buy) the contract.
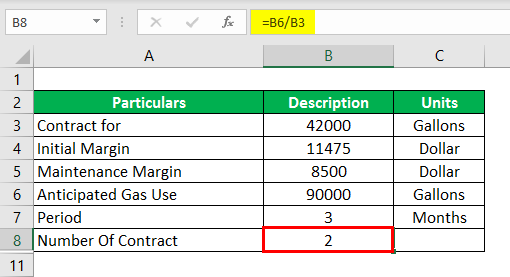
Question 2 – How many contracts should ABC Co. use?
Solution:
ABC Co. uses 90,000 Gallons of Gas every Month, and each Contract was for 42,000 Gallons.
- Number of Contracts = Anticipated Gas Use / Contract for
- Number of Contracts = 90000/42000
- Number of Contracts = 2
For Two Contracts:
- One contract = 42,000
- Two contracts = 2 × 42,000
- Two contracts = 84,000 Gallons of Gas.
So how many should be used? The answer is 2.
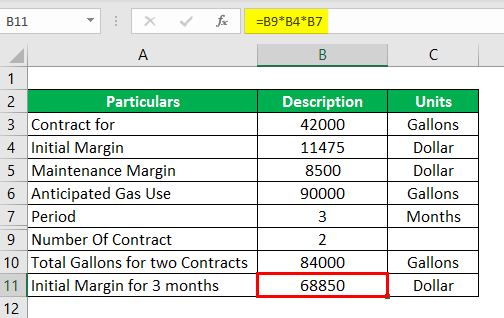
Question 3 -What is ABC Co.’s initial cash flow?
Initial Cash Flow or Margine is Calculated as :
Solution:
- So here a number of Contract = 2
- Initial Cash Flow/Margin = $11,475
- = 2 × $11,475
- = $22,950 per month
So for 3 month
- Initial Cash Flow/ Margin For 3 months = $22,950 × 3
- Initial Cash Flow /Margin For 3 months = $68,850
So initially, ABC Co. has to put $68,850 into its margin accounts to establish its position, giving the company two contacts for the next 3 months.
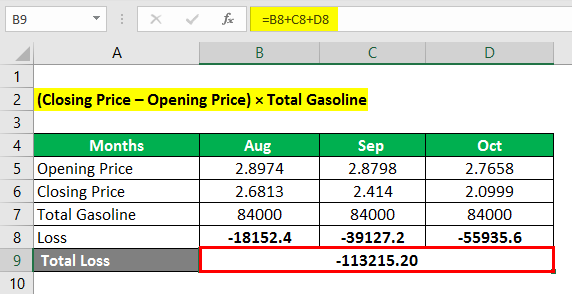
Question 4 – The price of gasoline for the August future is $2.8974, September future is $2.8798, and the October future is $2.7658 and which closed at August $2.6813, September $2.4140 and October $2.0999. How much did ABC Co. lose on a futures contract?
Solution:
Loss = (Closing Price – Opening Price) × Total Gasoline
Loss is Calculated as Below:
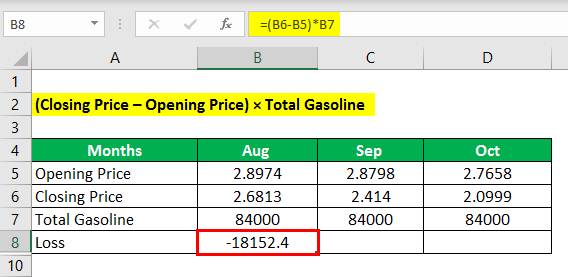
- Loss = (2.6813-2.8974) * 84000
- Loss = -18152.4
Similarly, for all,
- Total Loss = Loss In (Aug) + (Sep) + (Oct)
- Total Loss = -18152.4 + -39127.2 + -55935.6
- Total Loss = -113215.20
So Total loss on Futures Contracts is $-113215.20
Derivatives Example#2 – Long Futures
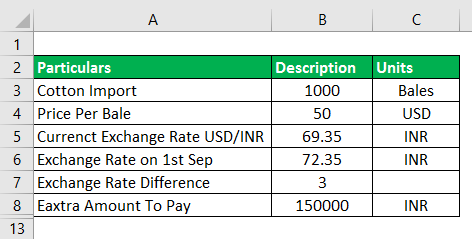
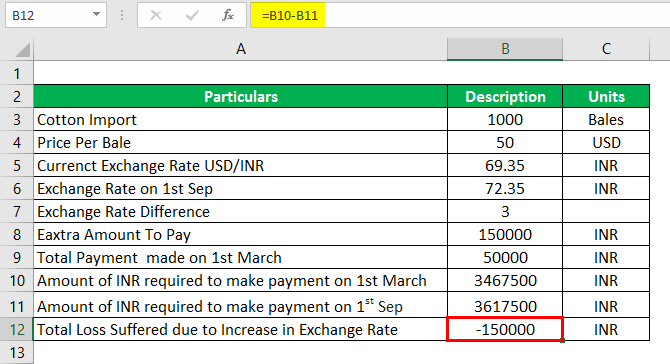
On 1st March, an Indian importer entered a contract to import 1,000 bales of cotton, with payments to be made in dollars on 1st September. The price of one bale of cotton was fixed at USD 50 per bale. The present exchange rate is 1 USD = 69.35 INR. The importer has the risk of paying more if the USD strengthens. The dollar strengthens in the coming months, and on the 1st of September, the exchange rate climbs to 1 USD = 72.35 INR. Let us look at the following two scenarios.
Now what has happened here is that Importer has to pay more due to a rate difference i.e. 72.35 INR – 69.35 INR = 3 INR
So 1000×50×3 = INR 1, 50,000 extra amount to pay.
Given,
Case -1:- When the Importer has not hedged his position.
Solution:
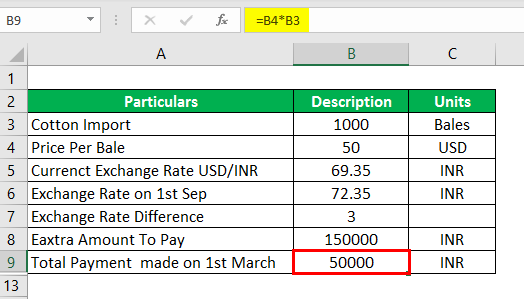
The Total Payment made in USD as of 1st March = No. Of cotton bales × per unit price
The Total Payment made in USD as of 1st March is as calculated below:
- The Total Payment Made on 1st March = 50×1000
- The Total Payment Made on 1st March = $50,000
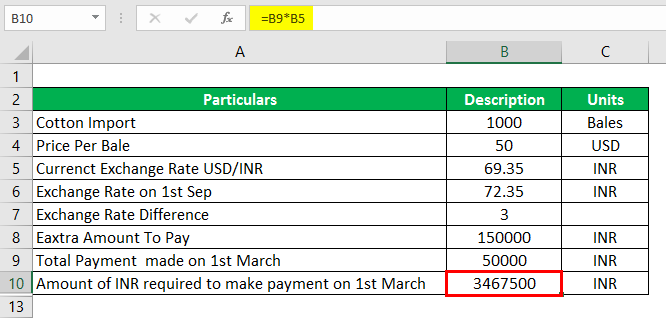
Amount of INR required to make a payment on 1st March
The amount of INR required to make a payment on 1st March is as calculated below:
- Amount of INR Required to make a Payment on 1st March = $50,000 × 69.35
- Amount of INR Required to make a Payment on 1st March = 34, 67,500 INR
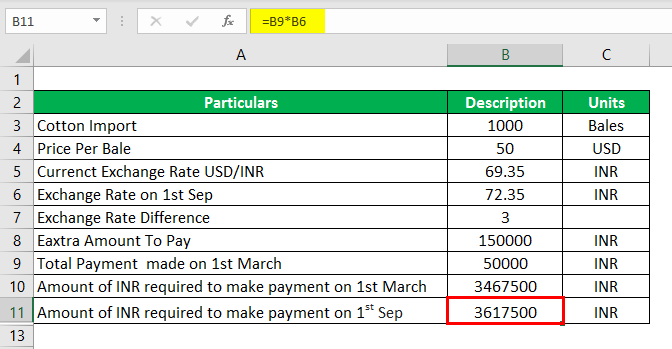
Amount of INR Required to Make a Payment on 1st Sep
- Amount of INR Required to make a Payment on 1st Sep = $50,000 × 72.35
- Amount of INR Required to make a Payment on 1st Sep = 36, 17,500 INR
Total Loss Suffered Due to an increase in the Exchange Rate
- Total Loss Suffered due to an increase in the Exchange Rate = 34, 67,500.00 – 36, 17,500.00
- Total Loss Suffered due to an increase in the Exchange Rate = -1, 50,000 INR
Conclusion– The Importer has to pay an extra 1 50,000.00 INR on 1st September due to an increase in the exchange rate, thus incurring a loss compared to his payment obligation on 1st March.
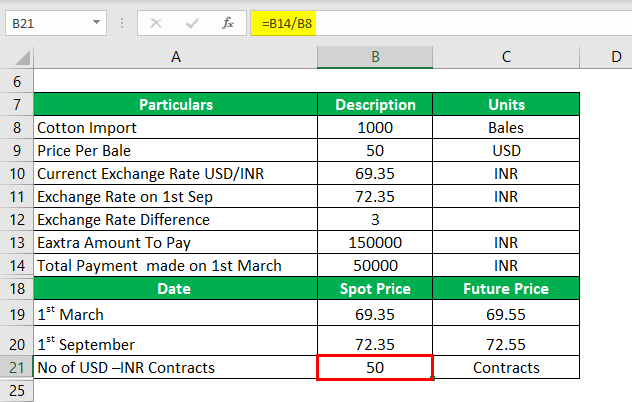
Case -2:- The Importer decided to hedge his position by going into the currency futures market. The importer expected that USD would strengthen, and he decided to USD-INR contract to hedge his position.
Solution:
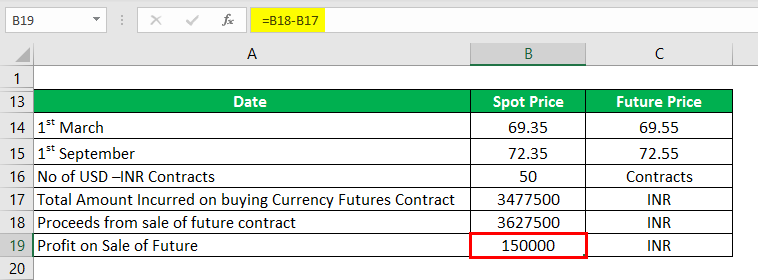
No USD –INR Contracts
No of USD –INR Contracts are calculated as:
- No of USD –INR Contracts = Amount to Pay/1000 (Lot size for 1USD-INR Contract)
- No of USD –INR Contracts = 50,000/1000
- No of USD –INR Contracts = 50 Contracts
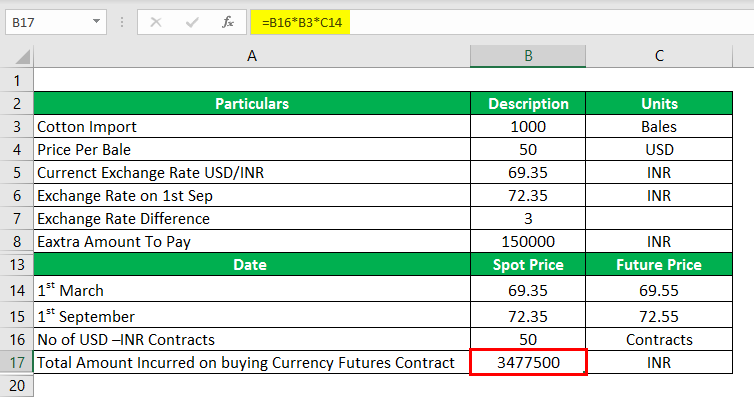
Total Amount Incurred on Buying a Currency Futures Contract
The total Amount Incurred on buying a Currency Futures Contract is calculated as :
- Total Amount Incurred on buying a Currency Futures Contract = 50 × 1000 × 69.55
- Total Amount Incurred on buying a Currency Futures Contract = 34, 77,500 INR
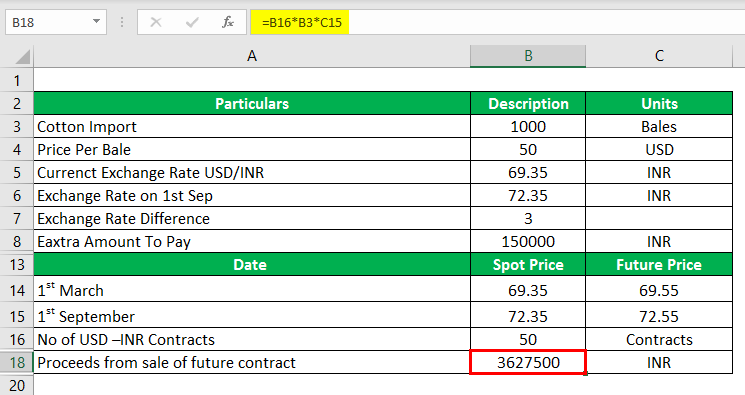
Proceeds from the Sale of Future Contract
Proceeds from the Sale of Future Contract is Calculated as :
On 1st September, the Exchange Rate moves to 72.35, and the Future Price Moves to 72.55
- Proceeds from the Sale of Future Contract = 50 × 1000 × 72.55
- Proceeds from the Sale of Future Contract = 36, 27,500 INR
Profit on Sale of Future
Profit on Sale of Future is calculated as :
Profit on Sale of Future = Sale of Future Contract – Purchase of Future Contract
- Profit on Sale of Future = 36, 27,500.00 – 34, 77,500.00
- Profit on Sale of Future = 1, 50,000 INR
Conclusion: The Importer has effectively hedged his loss by entering into future contracts and thereby null and void his loss because of adverse movement in the exchange rate.
Derivatives Example#3 – Stock Index Futures
John owns a stock portfolio, and detail related to the portfolio as mentioned below.
- Value of portfolio: V =$95 Million (Spot Price)
- Beta of portfolio: β =0.90
Future contract S&P Future price:
- f= 1,513.40
- S&P futures contract has a size of multiple of $250
- So future contract price = $250 × $1,513.40 = $378,350
- Note contract size = $250 × S&P futures price.
Solution:
Hedge Ratio (HR) = (S/f) β
- HR = (Dollar value of portfolio/Dollar price of S&P Futures contract) × β
- HR = ($95,000,000/$378,350) × 0.90
- HR= 225.98 ≈ 226
Now let’s try to understand the above example through below two scenarios:
Suppose the Market fall by, say 5%
Since John owns a portfolio, he will lose the money due to a fall in the market by 5%, but since John is short in the future (Sold Futures), he makes it again.
- Stock portfolio value fall by = β × 5%
- Stock portfolio value fall by = 0.9 × 5% = 4.5% or by 0.045 × $95,000,000)
- Stock portfolio value fall by = -$4,275,000
The futures Contract Price will also decrease by 5% so it will be $378,350 × 5% = $18,917.50
- Futures Contract Price = $378,350 – $18,917.50
- Futures Contract Price = $359,432.50
Futures Gain = ($378,350 – $359,432.50) × 226 = $4,275,355
- Hedge Profit = Spot Position + Future Position
- Hedge Profit = -$4,275,000 + $4,275,355
- Hedge Profit = $355
Suppose the Market rise by, say, 5%
Since John owns a portfolio, he will gain the money due to a rise in the market by 5%, but since John is short in futures (Sold Futures), he will lose.
- Stock portfolio value rise by = β × 5%
- Stock portfolio value rise by = 0.9 × 5% = 4.5% or by 0.045 × $95,000,000)
- Stock portfolio value rise by = $4,275,000
Future Contract Price will also rise by 5%, so it will be $378,350 × 5% = $18,917.50
- Future Contract Price = $378,350 + $18,917.50
- Future Contract Price = $ 397,267.50
Future Loss = ($378,350 – $397,267.50) × 226 = -$4,275,355
- Hedge Loss = Spot Position + Future Position
- Hedge Loss = $4,275,000 + (-$4,275,355)
- Hedge Loss = -$355
Conclusion
So the above examples give us a brief overview of how derivative markets work and how it hedges the risk in the market. The above examples show us that derivatives provide an efficient method for end-users to better hedge and manage their exposures to fluctuation in the market price/rates. The risks faced by derivative dealers depend on the actual strategy the dealer adopts. The above examples explain how hedging protects the hedger from unfavorable price movements while allowing continued participation in favorable movements. The above examples clarify that derivative is distinctly more complex than traditional financial instruments, such as stocks, bonds, loans, bank deposits, etc.
Recommended Articles
This has been a guide to Derivative Examples. Here we have discussed the top 3 examples of derivatives and a detailed explanation. You can also go through our other suggested article to learn more: