Updated July 27, 2023
Definition of Compound Interest Example
There are sample examples of compound interest. The following different compound interest example explains the most common situations to calculate compound interest. As there are multiple areas and situations where compound interest can be calculated, it is not possible to provide all the types of examples. So, the following examples explain step-by-step detail for calculating compound interest.
Examples of Compound Interest (With Excel Template)
Let’s take an example to understand the calculation of Compound Interest in a better manner.
Compound Interest Example -1
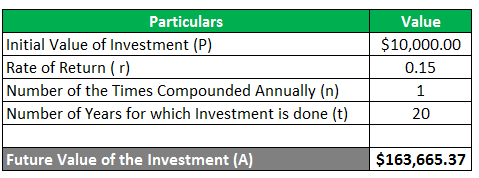
Harry wants to start the savings out of the money earned by him. He then deposits the initial $ 10,000 into the high-interest savings account. In this case, the interest rate is 15 % per annum compounded yearly. Currently, the age of Harry is 40 years, and he plans to take retirement at the age of 60 years. This means that Harry has a time horizon of 40 years over which he can accumulate interest. Calculate the amount of money Harry will receive at the age of 60 years. Also, prepare the table to show the yearly interest and Account value.
Given,
Solution:
The calculation of the compound interest and the amount value at the age of 60 years is as follows:
Calculation of the Future Value of Investment using the Compound Interest Formula is as below:
A = P (1 + r / n) nt
- A = $ 10,000 (1 + 0.15 / 1) 1*20
- A = $ 10,000 (1 + 0.15) 20
- A = $ 10,000 (1.15) 20
- A = $ 10,000 * 16.367
- A = $ 163,665.37
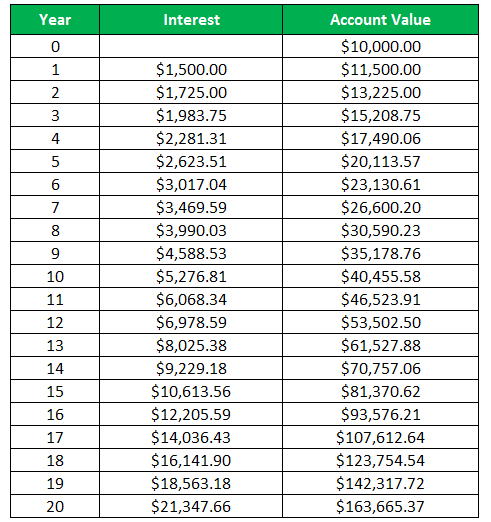
Table to show the yearly interest and Account value
Here, the formula to calculate interest is as follows:
- Interest = Initial Amount of Investment * Interest Rate (r)
- Interest = 10000*15%
- Interest = $1500
Similarly, for all Years.
And the Account Value is Calculate as:
- Account Value = Initial Amount of Investment + Interest
- Account Value = 10000 + 1500
- Account Value = $11500
Similarly, for all Years.
In the present example, we can see that the initial account value of the initial investment of $ 10,000 becomes $ 163,665.37 at the end of the 20-year period. This highlights the power of compounding, as with the help of compound interest, Harry multiplied his money to many folds without managing the investment actively. Here Harry could earn the interest on the previously earned interest as well.
Compound Interest Example -2
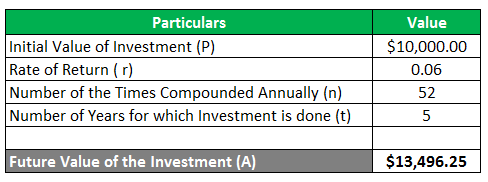
Sam makes an initial investment of $ 10,000 for a period of 5 years. He wants to know the amount of investment he will get after the 5 years if the investment earns a return of 6 % per annum compounded weekly.
Given,
The calculation of the compound interest and the amount value after the period of 5 years is as follows:
Solution:
Calculation of the future value of an investment using the compound interest formula is as below:
A = P (1 + r / n) nt
A = $ 10,000 (1 + 0.6 / 52) 52*5
A = $ 10,000 (1 + 0.00115) 260
A = $ 10,000 (1.00115) 260
A = $ 10,000 * 1.3496
A = $ 13,496.25
In the present example, we can see that the initial account value of the initial investment of $ 10,000 becomes $ 13,496.25 at the end of the 5-year period when the compounding is done weekly. The compounding increases the value of the investment at the end of the period as interest is earned on the previously earned interest as well. Here the compounding is done 52 times, as there are 52 weeks in a year.
Conclusion – Compound Interest Example
Compound interest gives more interest than simple interest as it charges interest on the outstanding principal, including interest. In contrast, simple interest charges interest solely on the original principal amount and does not accumulate interest on interest. The power of compounding helps grow the investment with more speed having the features of the exponential function. Companies utilize reinvesting funds to facilitate faster growth even after repaying the investment. It is a common practice in business, whether it involves loans or deposits. Additionally, the frequency at which compounding is done also significantly determines the growth rate.
Suppose if, at any given rate, the compounding frequency is per month, then its annualized rate will be more than that of the compounding frequency semi-annually or annually.
Recommended Articles
This article has been a guide to the Compound Interest Example. Here we discuss how to calculate compound interest using its formula along with practical examples. You may also have a look at the following articles to learn more –