Updated July 25, 2023
Convexity Formula (Table of Contents)
What is Convexity Formula?
The term “convexity” refers to the higher sensitivity of the bond price to the changes in the interest rate. In other words, the convexity captures the inverse relationship between the yield of a bond and its price wherein the change in bond price is higher than the change in the interest rate.
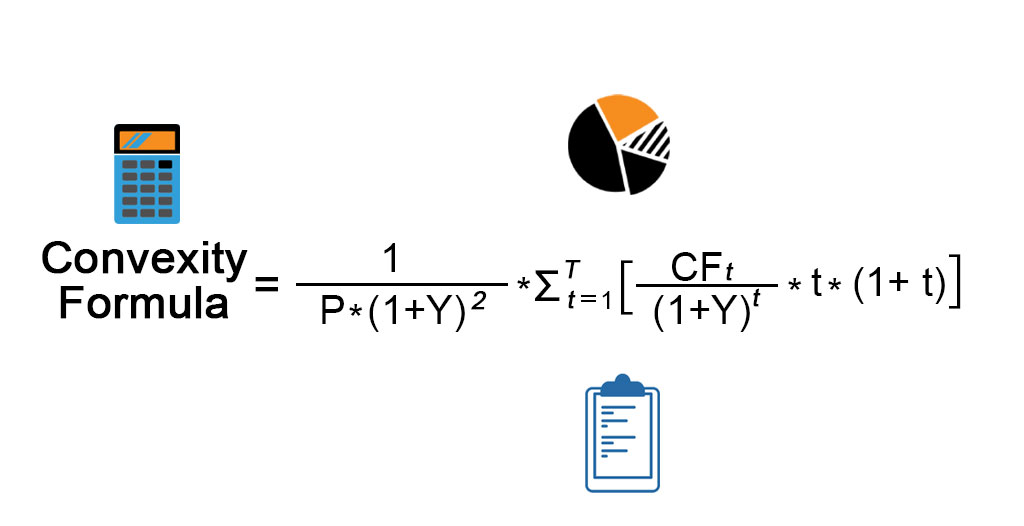
The formula for convexity is a complex one that uses the bond price, yield to maturity, time to maturity and discounted future cash inflow of the bond. The cash inflow includes both coupon payment and the principal received at maturity. Mathematically, the formula for convexity is represented as,
Where,
- CFt = Cash inflow in the tth Period (coupon payment and principal at maturity)
- P = Bond Price
- Y = Periodic Yield to Maturity
- t = Number of Periods
- T = Time to Maturity
Examples of Convexity Formula (With Excel Template)
Let’s take an example to understand the calculation of Convexity in a better manner.
Convexity Formula – Example #1
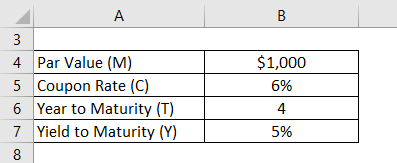
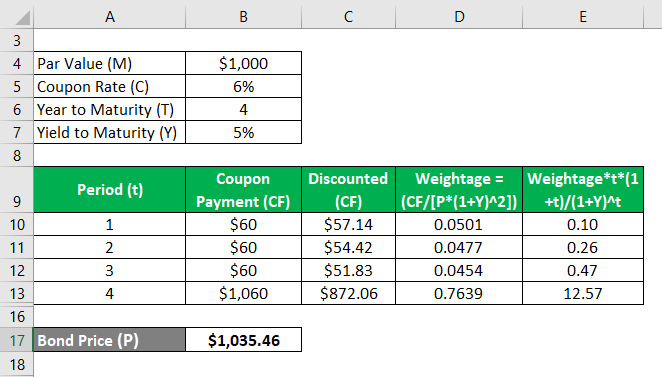
Let us take the example of a bond that pays an annual coupon of 6% and will mature in 4 years with a par value of $1,000. Calculate the convexity of the bond if the yield to maturity is 5%.
Solution:
Discounted (CF) is calculated as
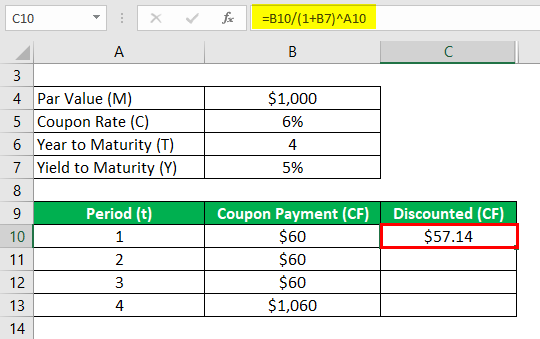
- Discounted (CF) = $60 / (1 + 5% ) 1
- Discounted (CF) = $57.14
Similarly, calculate it for all periods.
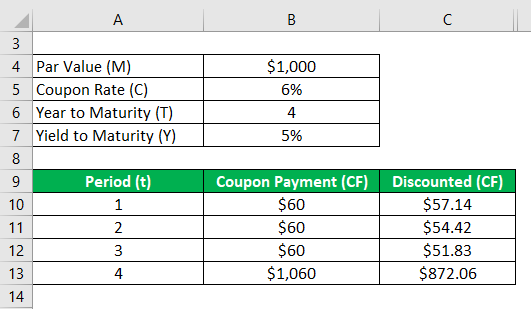
Bond Price (P) is calculated as
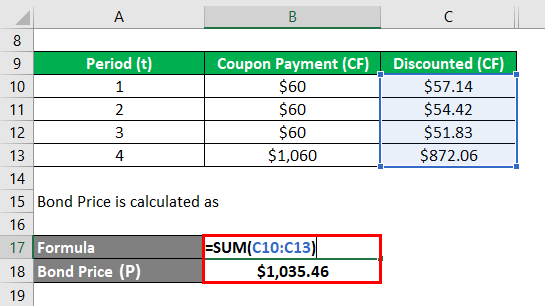
- Bond Price (P) = $57.14 + $54.42 + $51.83 + $872.06
- Bond Price (P) = $1,035.46
Convexity is calculated as
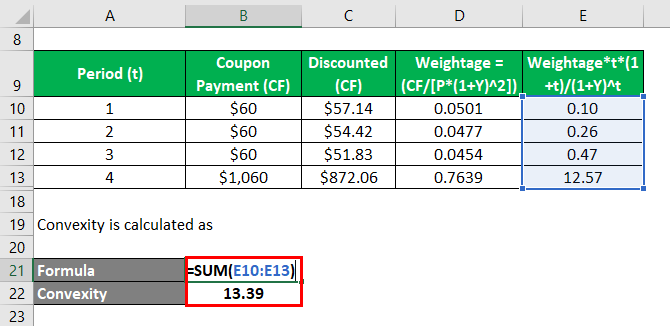
- Convexity = 0.10 + 0.26 + 0.47 + 12.57
- Convexity = 13.39
Therefore, the convexity of the bond is 13.39.
+
Let us take the example of the same bond while changing the number of payments to 2 i.e. semi-annual coupon payment. Calculate the convexity of the bond in this case.
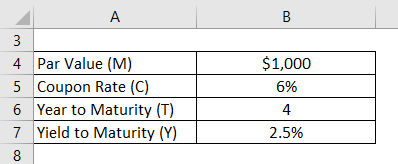
Periodic yield to maturity, Y = 5% / 2 = 2.5%
Solution:
Discounted (CF) is calculated as
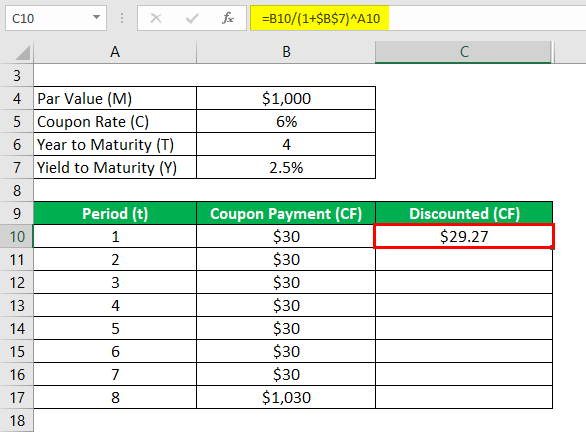
- Discounted (CF) = $30 / (1 + 2.5% ) 1
- Discounted (CF) = $29.27
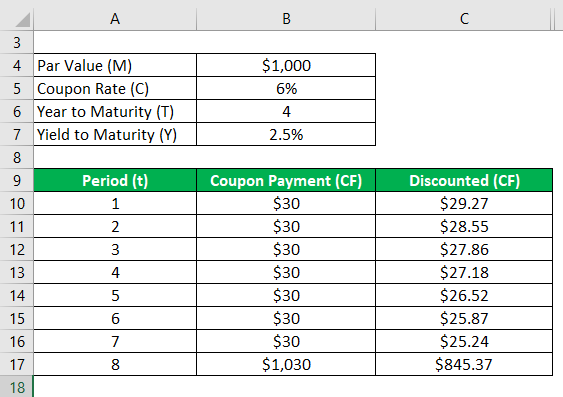
Similarly, calculate it for all periods.
Bond Price (P) is calculated as
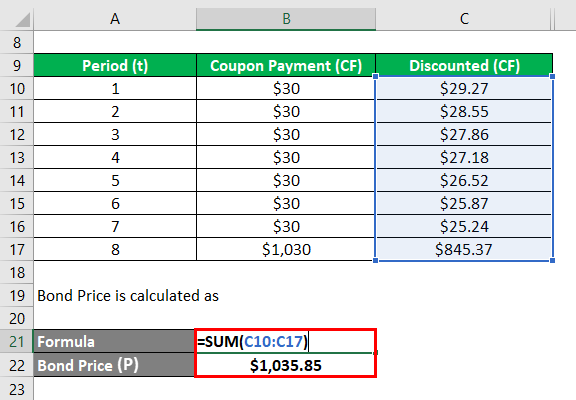
- Bond Price (P) = $29.27 + $28.55 + $27.86 + $27.18 + $26.52 + $25.87 + $25.24 + $845.37
- Bond Price (P) = $1,035.46
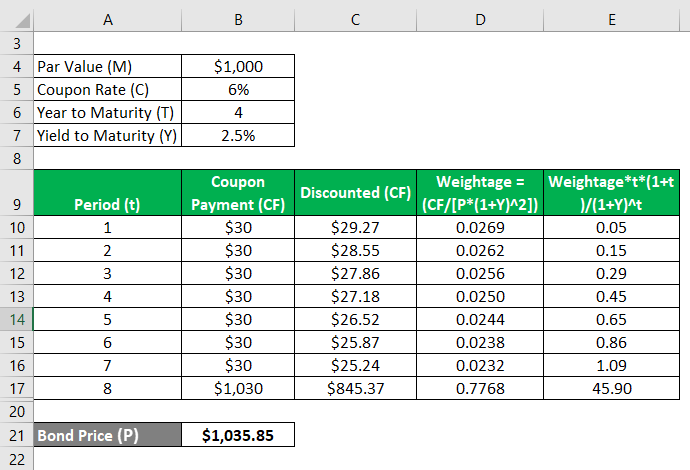
Convexity is calculated as
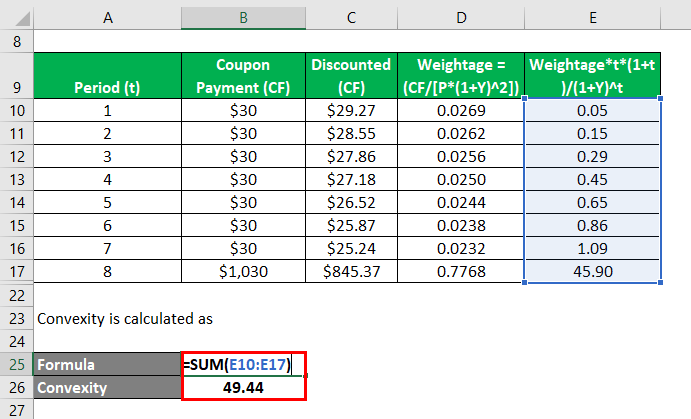
- Convexity = 0.05 + 0.15 + 0.29 + 0.45 + 0.65 + 0.86 + 1.09 + 45.90
- Convexity = 49.44
Therefore, the convexity of the bond has changed from 13.39 to 49.44 with the change in the frequency of coupon payment from annual to semi-annual.
Explanation
The formula for convexity can be computed by using the following steps:
Step 1: Firstly, determine the price of the bond which is denoted by P.
Step 2: Next, determine the frequency of the coupon payment or the number of payments made during a year.
Step 3: Next, determine the yield to maturity of the bond based on the ongoing market rate for bonds with similar risk profiles. The yield to maturity adjusted for the periodic payment is denoted by Y.
Step 4: Next, determine the total number of periods till maturity which can be computed by multiplying the number of years till maturity and the number of payments during a year. The time to maturity is denoted by T.
Step 5: Next, determine the cash inflow during each period which is denoted by CFt. The cash inflow will comprise all the coupon payments and par value at the maturity of the bond. The cash inflow is discounted by using yield to maturity and the corresponding period.
Step 6: Finally, the formula can be derived by using the bond price (step 1), yield to maturity (step 3), time to maturity (step 4) and discounted future cash inflow of the bond (step 5) as shown below.
Convexity = [1 / (P *(1+Y)2)] * Σ [(CFt / (1 + Y)t ) * t * (1+t)]
Relevance and Use of Convexity Formula
It is important to understand the concept of convexity of a bond as it is used by most investors to assess the bond’s sensitivity to changes in interest rates. The interest rate and the bond price move in opposite directions and as such bond price falls when the interest rate increases and vice versa.
Recommended Articles
This is a guide to Convexity Formula. Here we discuss how to calculate the convexity formula along with practical examples. we also provide a downloadable Excel template. You may also look at the following articles to learn more –

