Updated March 18, 2023
Introduction to BFS Algorithm
BFS Algorithm is known as (Breath-First Search) for traversing a graph. This algorithm helps to reach the specific node or through the vertex route of the data structure. The BFS algorithm works horizontally for the particular layer and moves to the next layer afterward. The major task of the algorithm is to find the shortest path in a graph while traversing. In the scenario where the graph involves a cyclic structure, it is good to add a Boolean array to mark the node once it is completed the traversal. There are several implementations of BFS algorithms through queue-based applications and other related data structures.
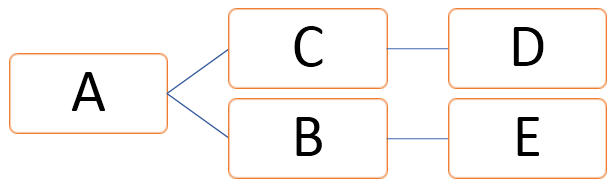
Nodes in Graph can also be referred to as vertices which are finite in number, and edges are the connecting lines between any two nodes.
In the above graph, vertices can be represented as V = {A, B, C, D, E} and edges can be defined as
E = {AB, AC, CD, BE}
What is the BFS Algorithm?
There are generally two algorithms that are used for the traversal of a graph. They are BFS (Breadth-First Search) and DFS (Depth First Search) algorithms. Traversal of the Graph is visiting exactly once each vertex or node and edge, in a well-defined order. It is also essential to keep track of the vertices that have been visited so that the same vertex is not traversed twice. To ensure the algorithm visits each vertex only once and to prevent the cycles in the graph, the vertices are divided into two categories:
1. Visited Vertices
2. Non-Visited Vertices
Each vertex can either be a visited or non-visited state, during the execution of the BFS algorithm. A vertex is deemed to have been visited when its neighbor is added to the queue after it has been dequeued from the queue.
In the Breath First Search algorithm, the traversing starts from a selected node or source node, and the traversal continues through the nodes directly connected to the source node. In simpler terms, in the BFS algorithm, one should first horizontally move and traverse the current layer after moving to the next layer.
How does BFS Algorithm Works?
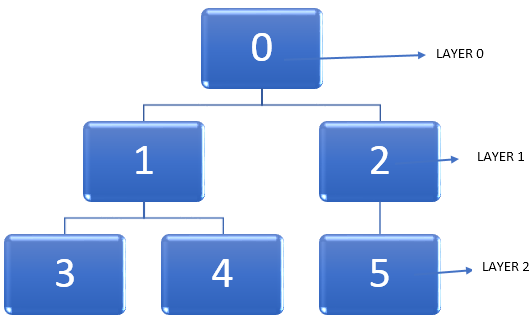
Let us take the example of the below graph.
The important task at hand is to find the shortest path in a graph while traversing the nodes. When we traverse through a graph, the vertex goes from an undiscovered state to discovered state and finally becomes completely discovered. It is to be noted that it is possible to get stuck at some point while traversing through a graph, and a node can be visited twice. So we can employ a method of marking the nodes after it changes the state of being undiscovered to being completely discovered.
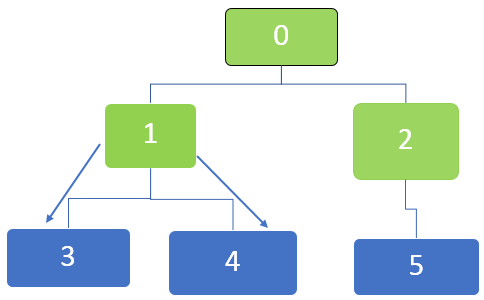
In the below image, we can see that the nodes can be marked in the graphs as they become completely discovered by marking them with black. We can start at the source node, and as the traversal progresses through each node, they can be marked to be identified.
The traversal starts from a vertex and then travels to the outgoing edges. When an edge goes to an undiscovered vertex, it is marked as discovered. But when an edge goes to a completely discovered or discovered vertex, it is ignored.
For a directed graph, each edge is visited once and for an undirected graph, it is visited twice, i.e. once while visiting each node. The algorithm to be used is decided based on how the discovered vertices are stored. In the BFS algorithm, the queue is used where the oldest vertex is discovered first and then propagates through the starting vertex layers.
Steps Performed for a BFS Algorithm
For the BFS algorithm, the steps below are executed.
- In a given graph, let us start from a vertex, i.e. in the above diagram; it is node 0. The level in which this vertex is present can be denoted as Layer 0.
- The next step is to find all the other vertices that are adjacent to the starting vertex, i.e. node 0 or immediately accessible from it. Then we can mark these adjacent vertices to be present at Layer 1.
- It is possible to come to the same vertex due to a loop in the graph. So, we should travel only to those vertices which should be present in the same layer.
- Next, the parent vertex of the current vertex that we are at is marked. The same is to be performed for all the vertices at Layer 1.
- The next step is to find all those vertices that are a single edge away from all the vertices at Layer 1. This new set of vertices will be at Layer 2.
- The above process is repeated until all the nodes are traversed.
Example
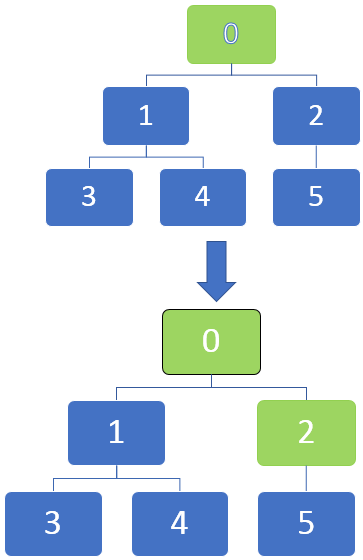
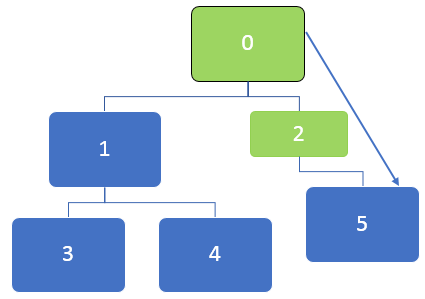
Let us take the example of the below graph and understand how the BFS algorithm works. Generally, in a BFS algorithm, a queue is used to en-queue the nodes while traversing the nodes.
In the above graph, first, the node 0 is to be visited, and this node is en-queued to the below queue:
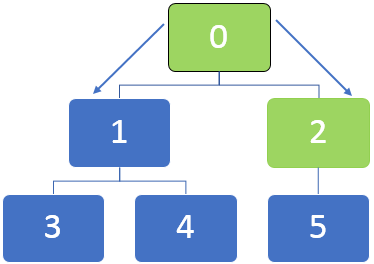
After visiting node 0, the neighbouring node of 0, 1 and 2 are en-queued. The queue can be represented as below:
Then the first node in the queue, which is 2, will be visited. After node 2 is visited, the queue can be represented as below:
After visiting node 2, 5 will be en-queued, and as there are no unvisited neighbouring nodes for node 5, still though 5 is en-queued, it will not be visited twice.
Next, the first node in the queue is 1, which will be visited. The neighbouring nodes 3 and 4 are en-queued. The queue is represented as below.
Next, the first node in the queue is 5, and for this node, there are no more unvisited neighbouring nodes. The same goes for nodes 3 and 4, for which there are no more unvisited neighbouring nodes too.
So all the nodes are traversed, and finally, the queue becomes empty.
Conclusion
Breadth Search Algorithm comes with some great advantages to recommend it. One of the many applications of the BFS algorithm is to calculate the shortest path. It is also used in networking to find neighbouring nodes and can be found in social networking sites, network broadcasting, and garbage collection. The users need to understand the requirement and the data pattern to use it for better performance.
Recommended Articles
This has been a guide to the BFS Algorithm. Here we discuss the basic concept, working, along with steps and examples of performance in the BFS Algorithm. You can also go through our other Suggested Articles to learn more –