Updated March 24, 2023
What is Matlab 3D Plots?
MATLAB is a language used for technical computing. As most of us will agree, an easy to use environment is a must for integrating tasks of computing, visualizing and finally programming. MATLAB does the same by providing an environment that is not only easy to use but also, the solutions that we get are displayed in terms of mathematical notations which most of us are familiar with.
Uses of MATLAB for Computing
MATLAB is used in many different ways, following are the list where it is commonly used.
- Computation
- Development of Algorithms
- Modeling
- Simulation
- Prototyping
- Data analytics (Analysis and Visualization of data)
- Engineering & Scientific graphics
- Application development
MATLAB provides its user with a basket of functions and tools, in this article we will understand About 3-dimensional plots in MATLAB.
- Plots are created for data visualization.
- Data visualization is very powerful in getting the look and feel of the data in just one glance.
- Data plots have a number of uses from comparing sets of data to tracking data changes over time.
Plots can be created using graphic functions or interactively using the MATLAB Desktop.
Types of 3D Plots in MATLAB
Below we have discussed the types of 3D plots in MATLAB used in computing.
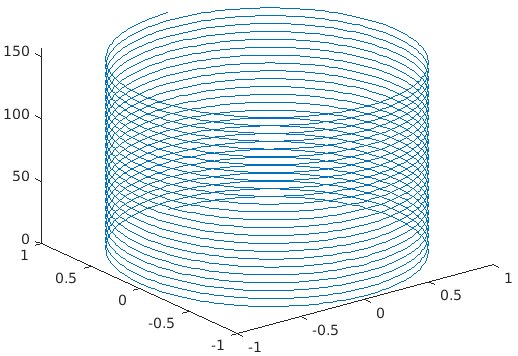
1. PLOT3 (Line Plots)
Plot3 helps in creating 3D lines or Point Plots.
Plot3(x,y,z): If x,y,z are vectors of the same length, then this function will create a set of coordinates connected by line segments. If we specify at least one of x, y or z as vectors, it will plot multiple sets of coordinates for the same set of axes.
Code:
A= 0: pi/100; 50*pi;
sa= sin(a);
ca=cos(a);
plot3(sa, ca, a)
Output:
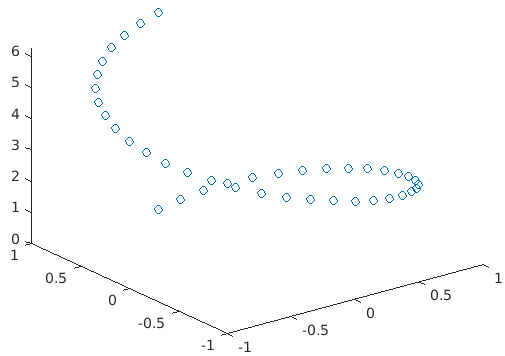
plot3(X, Y, Z, LineSpec): This function will create the plot using the specified line style, marker, and color.
Code:
A= 0:pi/20:2*pi;
sa= sin(a);
ca=cos(a) ;
plot3(sa, ca, a, ’o’)
Output:
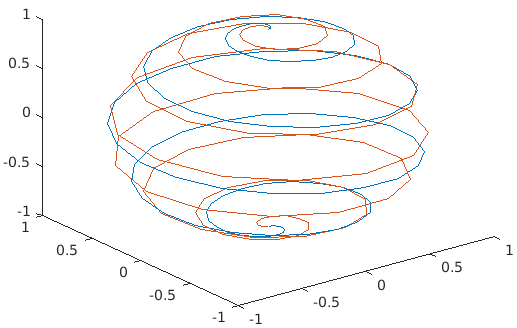
plot3(X1, Y1, Z1,…, Xn, Yn, Zn): This function will plot multiple coordinates for the same set of axes.
Code:
a= 0:pi/100*pi;
xa1= sin(a).cos(10*a);
ya1=sin(a).*sin(10*a) ;
za1=cos(a);
xa2= sin(a).cos(15*a);
ya2=sin(a).*sin(15*a) ;
za2=cos(a);
Plot3(xa1,ya1,za1,xa2,ya2,za2)
Output:
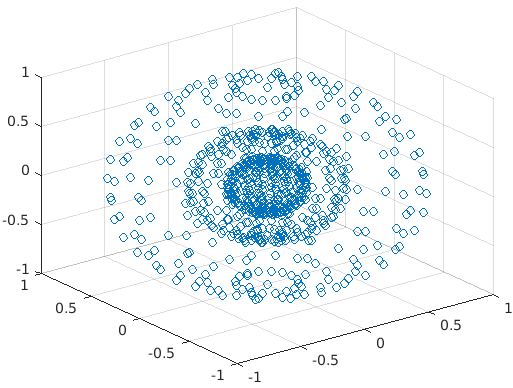
2. SCATTER3 (3D scatter Plot)
scatter3(X, Y, Z): This function will create circles at the vector locations of x, y, and z.
Example:
X, y, z are vector spheres.
Code:
[X,Y,Z] = SPHERE(10)
x = [0.5*X(:); 0.25*X(:); X(:)];
y = [0.5*Y(:); 0.25*Y(:); Y(:)];
z = [0.5*Z(:); 0.25*Z(:); Z(:)];
Output:
scatter3(X, Y, Z, A, C): This function will create a plot with a circle that will have size A from the argument. If A is scalar, the size of the circles will be equal. For the specific size of the circle, we will have to define A as a vector.
Code:
[X, Y, Z] = sphere(20);
x = [0.5*X(:); 0.75*X(:); X(:)];
y = [0.5*Y(:); 0.75*Y(:); Y(:)];
z = [0.5*Z(:); 0.75*Z(:); Z(:)];
scatter3(x, y, z)
Define a vector to specify the marker sizes.
a = repmat([50,10,2],numel(X),1);
C = repmat([1,2,3],numel(X),1);
a = a(:);
c = c(:);
Output:
3. CONTOUR3 (3D contour plots)
contour3(Z): Z is a matrix and this function will create a 3-D contour plot which will have the isolines of matrix z will have the height details of x and y plane. The x & y coordinates in the plane are column and row indices of Z. Contour lines are selected by MATLAB automatically.
Code:
[X,Y] = meshgrid(-1:0.20:2);
Z = X.^2 + Y.^2;
contour3(Z)
Output:
Define contour levels as 30, and display the results within x and y limits.
Code:
Contour3(X,Y,Z,30)
Output:
4. QUIVER3 (Velocity Plot)
3D quiver plot creates vectors with components (u,v,w) at the points (x,y,z), where u, v, w, x, y, and z are real values.
Code:
x = -3:0.5:3;
y = -3:0.5:3;
[X,Y] = meshgrid(x, y);
Z = Y.^2 - X.^2;
[U,V,W] = surfnorm(Z);
Output:
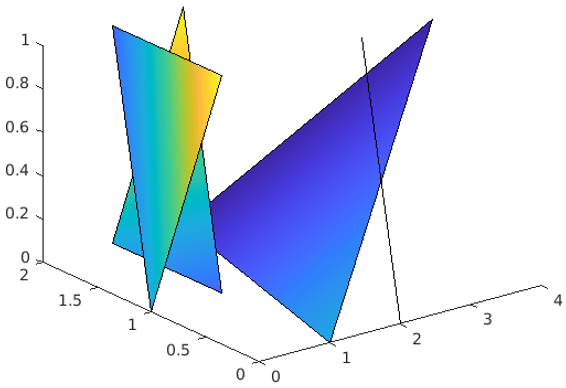
5. FILL3 (3D filled polygon plot)
This function helps in creating flat shaped and Gouraud polygons (to get different shades of light).
fill3(X, Y, Z, C): It helps in creating filled polygons with vertices x, y, z. The x, y, z values can be number, duration, and DateTime, etc.
Code:
X = [1 2 3 4; 1 1 3 2; 0 1 2 1];
Y = [2 2 1 1; 1 2 1 2; 1 1 0 0];
Z = [1 1 1 1; 1 0 1 0; 0 0 0 0];
C = [0.5000 1.0000 1.0000 0.5000;
1.0000 0.5000 0.5000 0.1667;
0.3330 0.3330 0.5000 0.5000];
Output:
In the above figure, we can clearly see the Gouraud effect.
Conclusion – 3D Plots in Matlab
Data visualization becomes a very powerful technique when we have to understand how our data is behaving. It also tells us visually, how a particular function is changing when it is supplied with different values. 3 D plot in MATLAB is a tool which is very helpful in visualizing the behavior of data.
Recommended Articles
This is a guide to 3D Plots in Matlab. Here we discuss what is Matlab, uses Matlab and types of 3D plot in Matlab for computing. You can also go through our other related articles to learn more –