Z Score Formula

Z Score Formula (Table of Contents)

• Formula
• Examples
• Calculator

What is Z Score Formula?

The “Z score” is one of the most widely used statistical tools that is used to standardize score, provided population means and the standard deviation is known. As such, the Z score is also known as the standard score. The Z score varies in the range of -3 times the standard deviation to +3 times the standard deviation with a mean of zero and a standard deviation of one. The formula for the Z score of a variable can be derived by deducting the mean of the population from the given variable (which is a part of the data set or population) and then dividing the result by the standard deviation of the population.

Mathematically, it is represented as:

where,

• X = Variable from the population.
• μ = Mean of the population.
• σ = Standard deviation of the population.

Examples of Z Score Formula (With Excel Template)

Let’s take an example to understand the calculation of the Z Score in a better manner.

Z Score Formula – Example #1

Let us take the example of Manny, who recently appeared for SAT. He managed to score 1109 in this attempt. However, as per available information, the average score for SAT remained around 1030 with a standard deviation of 250. Therefore, calculate the Z score for Manny’s SAT score and assess how well he did as compared to the average test-takers.

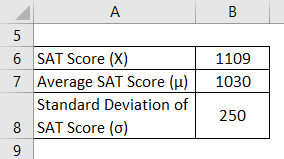
Solution:

Z Score is calculated using the formula given below:

Z = (X – μ) / σ

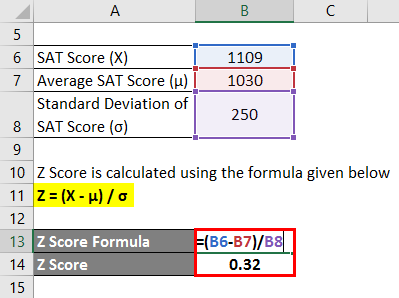
• Z Score = (1109 – 1030) / 250
• Z Score = 0.32

Therefore, Manny’s SAT score is 0.32 standard deviation higher than the average test-takers score, which indicates that 62.55% of the test takers scored less than Manny.

Z Score Formula – Example #2

Now, let us take the example of Chelsea, who has written the SAT twice and wants to compare her performance in them. She managed to score 1085 and 1059 in her 1^st and 2^nd attempts, respectively. According to available information, the average score and standard deviation during the 1^st attempt were 1100 and 230 respectively, while in the latter it was 1050 and 240 respectively. Please help Chelsea to decide in which exam did she perform better.

Solution:

1^st attempt

Z Score is calculated using the formula given below:

Z = (X – μ) / σ

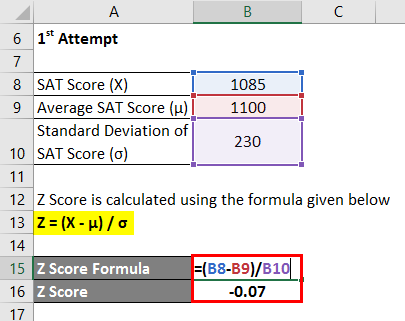
• Z Score = (1085 – 1100) / 230
• Z Score = -0.07

Therefore, Chelsea’s SAT score on 1^st attempt is 0.07 standard deviation lower than the average test-takers score, which indicates that 47.40% of the test takers scored less than Chelsea during the 1^st attempt.

2^nd attempt

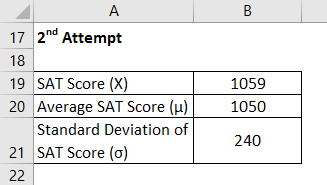
Z Score is calculated using the formula given below:

Z = (X – μ) / σ

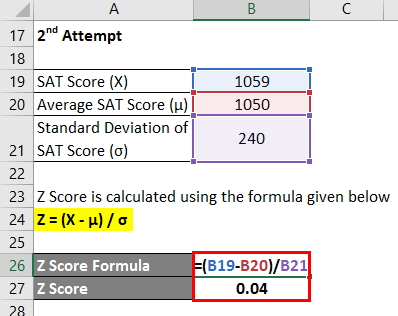
• Z Score = (1059 – 1050) / 240
• Z Score = 0.04

Therefore, Chelsea’s SAT score in the 2^nd attempt is 0.04 standard deviation higher than the average test-takers score, which indicates that 51.50% of the test takers scored less than Chelsea during the 2^nd attempt.

So, from the comparison of the Z scores, it is clear that Chelsea performed better during her 2^nd attempt.

Explanation

The formula for the Z score can be derived by using the following steps:

Step 1: Firstly, build a population with many variables and the variables denoted by X_i.

Step 2: Next, the number of variables in the population is calculated, and it is denoted by N.

Step 3: Next, the mean of the population is calculated by summing up all the variables followed by division by the total number of variables (step 2) in the data set. The mean of the population is denoted by μ.

μ = ∑ X_i / N

Step 4: Next, deduct the mean from each data set variable to calculate their deviation from the mean.

i.e. (X_i – μ) is the deviation for the i^th data point.

Step 5: Next, calculate the squared deviations for the variables, i.e. (X_i – μ)².

Step 6: Next, add up all the squared deviations and then divide the total by the number of variables in the data set to arrive at the variance.

σ² = ∑(X_i – μ)² / N

Step 7: Next, the population’s standard deviation is calculated by computing the square root of the variance calculated in the above step.

σ = √ ∑(X_i – μ)² / N

Step 8: Finally, the formula for the Z score is derived by deducting the mean of the population (step 3) from the variable and then dividing the result by the standard deviation of the population (step 7), as shown below.

Z = (X – μ) / σ

Relevance and Uses of Z Score Formula

From the perspective of a statistician, the concept of Z score is very important as it is useful in determining the probability of whether or not an event will occur within a normal distribution. In fact, the Z score is also used to compare two raw scores from two different normal distributions, and it is done by converting the raw scores into Z scores or standardized scores. Further, a positive Z score implies a score that is higher than the mean, while a negative Z score implies a score less than the mean.

Z Score Formula Calculator

You can use the following Z Score Formula Calculator

Recommended Articles

This has been a guide to Z Score Formula. Here we discuss how to calculate Z Score along with practical examples. We also provide a Z Score calculator with a downloadable excel template. You may also look at the following articles to learn more –

1. Examples of Sample Size Formula
2. Calculator For Correlation Formula
3. Formula to Calculate Normal Distribution
4. Examples of Altman Z Score