Topological Sorting in Python

Introduction

Have you ever gotten stuck building a bookshelf because you accidentally started with the top shelf? Or maybe you tried whipping up a delicious souffle, only to realize you forgot to separate the eggs? These, my friends, are classic dependency nightmares. In computer science, these scenarios translate to tasks with prerequisites – you can’t complete task B until you finish task A. This is where the ingenious concept of Topological Sorting in Python swoops in to save the day.

Topological sorting is an algorithm designed specifically for Directed Acyclic Graphs (DAGs). Don’t let the fancy term scare you – a DAG is simply a network of interconnected things (like tasks in a project) where arrows show dependencies, but there are no loops (you can’t build shelf B on top of shelf A if shelf A rests on B!).

This nifty algorithm helps you arrange these tasks in a linear order, ensuring you tackle prerequisites before diving into dependent steps. Think of it as a magic bullet for ensuring your project unfolds smoothly, one well-defined step at a time.

So, buckle up, Python enthusiasts! This article will equip you with the knowledge and code to conquer and master its techniques and empower you to tame the wildest dependency graphs with finesse and ease.

Table of Contents

• Introduction
  • Topological Sorting Python in Action
  • Understanding Directed Acyclic Graphs (DAGs)
  • Visual example of a simple DAG
  • Representing DAGs in Python
  • Python Implementation
  • Applications of Topological Sorting
  • Considerations and Extensions
  • Comparison with Other Sorting Algorithms
  • Limitations of Topological Sorting Algorithms

Topological Sorting Python in Action

Topological Sorting Python is a powerful algorithm used to arrange a directed acyclic graph (DAG) so that for every directed edge uv from vertex u to vertex v, u precedes v in the ordering. In simpler terms, Topological Sorting Python helps us organize tasks or nodes in a graph based on their dependencies, ultimately establishing a linear order and ensuring that no task executes before meeting its prerequisites.

Understanding Directed Acyclic Graphs (DAGs)

In a directed acyclic graph (DAG), you can list vertices in linear order such that vertex u comes before v for every directed edge (u,v). This linear ordering is a topological ordering in a directed acyclic graph (DAG). It is only possible in acyclic-directed graphs, i.e., DAGs. It means that the graph given must be directed and acyclic.

Depth-first search (DFS) and the Kahn algorithm are topological sorting algorithms. DFS-based topological sorting is recursive algorithm. It starts from a vertex with no incoming edges. Then, it adds the vertices to the list that are visited. We reverse the list to produce topological order. The Kahn algorithm uses a queue. The algorithm removes a vertex from the queue and adds it in topological order. Then, it adds all adjacent vertices of the removed vertex (with no incoming edges) to the queue. It terminates whenever the queue becomes empty. It means that all vertices have been processed.

Topological ordering has various applications:

• Task Scheduling: For project managers, it ensures tasks are completed in the correct order, eliminating errors caused by starting dependent steps too early (think software development!).
• Dependency Analysis: Identify potential roadblocks before they arise. Imagine a marketing campaign where website design relies on finalized messaging – Topological Sorting reveals this, allowing for smoother execution.
• Event Management: Establish a logical flow for presentations with cascading dependencies. Conference organizers can ensure a clear and cohesive attendee experience by prioritizing talks based on their conceptual connections.
• Deadlock Detection: Prevent frustrating situations where processes wait on each other indefinitely. Topological Sorting helps identify potential deadlocks in database transactions or other resource-sharing scenarios.
• Course Scheduling: Create course schedules that meet prerequisites. Universities can ensure students build a strong knowledge foundation by prioritizing courses like Calculus before Linear Algebra.

A directed acyclic graph (DAG) lacks cycles in its directed connections. Each directed edge in a DAG signifies a link from one vertex to another.

Formally, a DAG G = (V, E) has a set of vertices V and a set of directed edges E, where each edge (u,v) represents a directed connection from vertex u to vertex v. Importantly, a DAG does not contain any cycles, ensuring that no directed paths lead back to the same vertex.

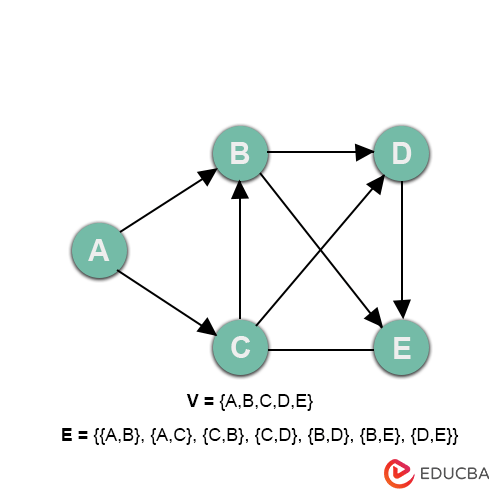
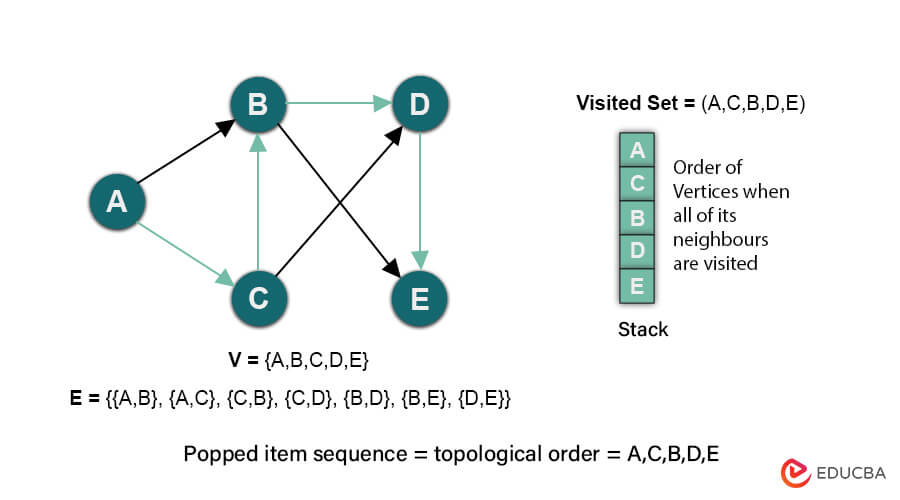
Visual example of a simple DAG

Consider the following graph,

In the directed edge {A, B}, vertex A is the starting vertex, and vertex B is the ending vertex. This vertex positioning is consistent across all directed edges.

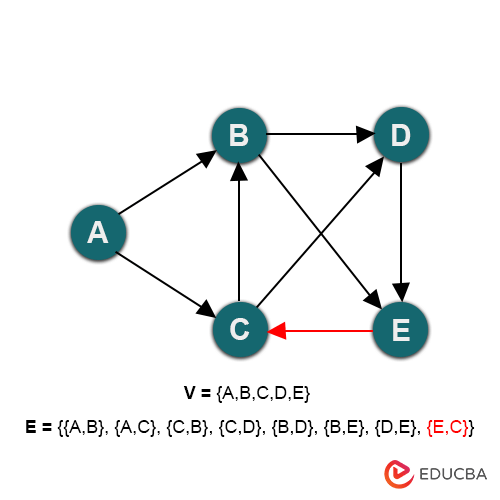
The above graph is directed and has no cycle, so this is a directed acyclic graph (DAG). But if you add an edge {E, C} to this graph, like this:

Now, this graph has a cycle or more than one cycle. For example, {{C,B}, {B,D}, {D,E}, {E,C}} is a cycle in this graph. So, it is not an acyclic graph; hence, it is not a DAG.

Representing DAGs in Python

Using different data structures, we will use the given DAG to represent it in Python.

1. Data Structures

In Python, various representations exist to represent DAGs. For example, you can use different data structures, such as lists and matrixes, to define a DAG.

(a). Using adjacency list

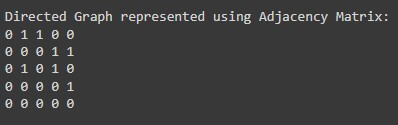
An adjacency matrix is a 2D matrix. Each cell represents whether there is an edge from one vertex to another. Here is the representation of the DAG as an adjacency matrix:

adjacency_list = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['B', 'D'],
    'D': ['E'],
    'E': []
}

(b). Using adjacency matrix (represented as a nested list)

An adjacency matrix is a 2D matrix. where, each cell represents whether there is an edge from one vertex to another. Here the representation of the DAG as a adjacency matrix:

adjacency_matrix = [
    [0, 1, 1, 0, 0],
    [0, 0, 0, 1, 1],
    [0, 1, 0, 1, 0],
    [0, 0, 0, 0, 1],
    [0, 0, 0, 0, 0]
]

(c). Using dictionary of sets

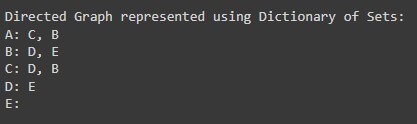
Each vertex serves as a key in this representation, storing its adjacent vertices in a set. Here’s the representation using a dictionary of sets:

adjacency_sets = {
    'A': {'B', 'C'},
    'B': {'D', 'E'},
    'C': {'B', 'D'},
    'D': {'E'},
    'E': set()
}

Note that we can also use a custom class to represent a DAG, which allows us to represent even more complex graphs. However, in this tutorial, we have discussed only the basic methods for representing a DAG.

2. Code Examples

(a). DAG representation using Adjacency List

class DirectedGraph:
    def __init__(self):
        self.adj_list = {}

    def add_edge(self, u, v):
        if u not in self.adj_list:
            self.adj_list[u] = []
        self.adj_list[u].append(v)

    def print_graph(self):
        for vertex, neighbors in self.adj_list.items():
            print(f"{vertex}: {', '.join(neighbors)}")

# Create a Directed Graph
dag_adj_list = DirectedGraph()

# Add edges
dag_adj_list.add_edge('A', 'B')
dag_adj_list.add_edge('A', 'C')
dag_adj_list.add_edge('C', 'B')
dag_adj_list.add_edge('C', 'D')
dag_adj_list.add_edge('B', 'D')
dag_adj_list.add_edge('B', 'E')
dag_adj_list.add_edge('D', 'E')

# Print the Directed Graph
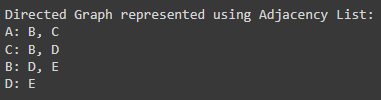
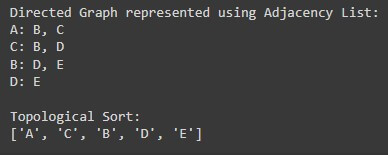
print("Directed Graph represented using Adjacency List:")
dag_adj_list.print_graph()

Output:

Explanation:

• We have defined the DirectedGraph class to represent a directed graph.
• It has a dictionary named adj_list, where vertices are keys and neighboring vertices are values.
• The adf_edge() method adds edge (u,v) to the dictionary. Here, u is the key, and v is the value.
• The print_graph() method iterate over graph vertices and prints vertex with its neighbors.
• We have created an instance dag_adj_list of the class DirectedGraph.
• We have added all the edges of the above DAG to this adjacency list.

(b). DAG representation using Adjacency Matrix

class DirectedGraph:
    def __init__(self, vertices):
        self.vertices = vertices
        self.adj_matrix = [[0] * len(vertices) for _ in range(len(vertices))]

    def add_edge(self, u, v):
        u_idx = self.vertices.index(u)
        v_idx = self.vertices.index(v)
        self.adj_matrix[u_idx][v_idx] = 1

    def print_graph(self):
        for row in self.adj_matrix:
            print(' '.join(map(str, row)))

# Create a Directed Graph
vertices = ['A', 'B', 'C', 'D', 'E']
dag_adj_matrix = DirectedGraph(vertices)

# Add edges
dag_adj_matrix.add_edge('A', 'B')
dag_adj_matrix.add_edge('A', 'C')
dag_adj_matrix.add_edge('C', 'B')
dag_adj_matrix.add_edge('C', 'D')
dag_adj_matrix.add_edge('B', 'D')
dag_adj_matrix.add_edge('B', 'E')
dag_adj_matrix.add_edge('D', 'E')

# Print the Directed Graph
print("\nDirected Graph represented using Adjacency Matrix:")
dag_adj_matrix.print_graph()

Output:

Explanation:

• We have defined DirectedGraph to represent a directed graph.
• The constructor (i.e., __init__()) initializes the adjacency matrix with the size of the vertices.
• An edge from vertex i to vertex j is represented by the value at position (i, j) in this matrix.
• The add_edge() method sets value 1 in the matrix if an edge extends from vertex i to vertex j.
• The print_graph() method iterates over matrix row by row and prints values.
• We have created a dag_adj_matrix instance of the DiredctedGraph class with a passing list of vertices [‘A,’ ‘B,’ ‘C,’ ‘D,’ ‘E’].
• We have added the given edges to this matrix.

(c). DAG representation using Adjacency Matrix

# Create a Directed Graph represented using Dictionary of Sets
dag_dict_of_sets = {
    'A': {'B', 'C'},
    'B': {'D', 'E'},
    'C': {'B', 'D'},
    'D': {'E'},
    'E': set()
}

# Print the Directed Graph
print("\nDirected Graph represented using Dictionary of Sets:")
for vertex, neighbors in dag_dict_of_sets.items():
    print(f"{vertex}: {', '.join(neighbors)}")

Output:

Explanation:

• We have created dag_dict_of_sets. It is a dictionary of sets.
• A vertex is a key, and a set of neighboring vertices is a value.
• We iterate over this dictionary of sets and print its values.

The Topological Sorting Algorithm

Topological sorting is the linear arrangement of vertices u precedes v in the ordering for each directed edge u -> v. It can be done only for Directed Acyclic Graphs (DAGs). We have a depth-first search (DFS) traversal algorithm for topological sorting. The vertices are visited recursively and pushed onto a stack in reverse order of their finishing times.

Algorithm

1. Initialize:

• Create an empty stack to store the vertices in topological order.
• Create a set to keep track of visited vertices.

2. Depth-First Search (DFS):

• Start DFS from any unvisited vertex.
• For each vertex encountered during DFS, recursively explore its neighbors.
• Mark each visited vertex as visited.
• When all neighbors of a vertex are visited, push that vertex onto the stack.

3. Output Topological Order:

• Once DFS traversal is completed for all vertices, pop vertices from the stack.
• The order in which vertices pop from the stack determines the topological order.

Pseudocode

function topologicalSort(graph):
    stack = []
    visited = set()

    function dfs(vertex):
        visited.add(vertex)
        for neighbor in graph.adj_list.get(vertex, []):
            if neighbor not in visited:
                dfs(neighbor)
        stack.append(vertex)

    for vertex in graph.adj_list:
        if vertex not in visited:
            dfs(vertex)

    return stack[::-1]

The algorithm recursively visits each vertex and its neighbors using DFS. After all vertices are visited, the stack contains vertices sorted in topological order. To obtain the final topological order, reverse the order of vertices in the stack.

Python Implementation

Code

class DirectedGraph:
    def __init__(self):
        self.adj_list = {}

    def add_edge(self, u, v):
        if u not in self.adj_list:
            self.adj_list[u] = []
        self.adj_list[u].append(v)

    def print_graph(self):
        for vertex, neighbors in self.adj_list.items():
            print(f"{vertex}: {', '.join(neighbors)}")

    def topological_sort_util(self, vertex, visited, stack):
        visited.add(vertex)

        for neighbor in self.adj_list.get(vertex, []):
            if neighbor not in visited:
                self.topological_sort_util(neighbor, visited, stack)

        stack.append(vertex)

    def topological_sort(self):
        visited = set()
        stack = []

        for vertex in self.adj_list:
            if vertex not in visited:
                self.topological_sort_util(vertex, visited, stack)

        return stack[::-1]

# Create a Directed Graph
dag_adj_list = DirectedGraph()

# Add edges
dag_adj_list.add_edge('A', 'B')
dag_adj_list.add_edge('A', 'C')
dag_adj_list.add_edge('C', 'B')
dag_adj_list.add_edge('C', 'D')
dag_adj_list.add_edge('B', 'D')
dag_adj_list.add_edge('B', 'E')
dag_adj_list.add_edge('D', 'E')

# Print the Directed Graph
print("Directed Graph represented using Adjacency List:")
dag_adj_list.print_graph()

# Perform topological sort
print("\nTopological Sort:")
print(dag_adj_list.topological_sort())

Output:

Explanation:

• We have extended DirectedGraph class as given above to represent DAG using Adjacency List.
• We have added the topological_sort() method for sorting using DFS (Depth First Search). It also has a topological_sort_util() method for recursive DFS traversal.
• We print the results of the topological sort.

Applications of Topological Sorting

1. Task Scheduling

Topological sorting is applicable for tasks that require completion before others can start. Topological sorting enables finding the order in which tasks should be completed to satisfy all dependencies.

2. Deadlock Detection

You can use topological sorting to detect deadlock in a system. It can detect circular dependencies that cause deadlock.

3. Course Planning

You can use topological sorting for course planning. It can schedule courses by identifying the order in which courses should be taken.

4. Event Management

Event management utilizes topological sorting. Various events may depend on each other. So, you can use topological sorting to find the correct order of event processing to avoid conflicts.

5. Network Routing

In computer networks, routing protocols may use topological sorting to construct routing tables. It can find the best path for data packets to travel through the network.

Considerations and Extensions

1. Cycle Detection

Topological sorting operates within directed acyclic graphs (DAGs). Therefore, you need to check for cycles in the graph first. Before applying topological sorting, you must detect and break the cycles for graphs with cycles.

2. Multiple Solutions

There are multiple topological orderings for a DAG. Applications may require exploring and considering all possible orderings based on specific requirements or constraints.

3. Performance Optimization

You can optimize the performance of topological sorting algorithms. You can use different techniques like memorization. You can also use parallel topological sorting in graphs with different root nodes.

Complexity Analysis

The DFS-based topological sorting algorithm:

• It is a simple and efficient algorithm.
• The time complexity is O(V + E). Because it visited each vertex exactly once and each edge at most once.
• The space complexity is O(V) because the algorithm uses a stack. The stack stores the vertices that have been visited but still need to be added to the topological order. In the worst case, the stack will contain all of the vertices in the graph.

Comparison with Other Sorting Algorithms

Sorting Algorithm	Characteristics	Uses
Topological Sorting	It is designed for directed acyclic graphs (DAGs).	Scheduling tasks with dependencies, dependency analysis, event management, deadlock detection, etc.
Depth-First Search (DFS)	It traverses as far as possible along each branch, backtracking when necessary.	Graph traversal, cycle detection, finding connected components, pathfinding, topological sorting.
Breadth-First Search (BFS)	It finds all neighbor nodes at the present depth before moving to the next depth level.	Shortest path finding, connected components, graph traversal, network broadcasting.
Kahn’s Algorithm	It iteratively selects vertices with no incoming edges, removes them, and adds them to the sorted list.	Topological sorting, task scheduling, dependency resolution.

Limitations of Topological Sorting Algorithms

1. It can be used only in DAG (directed acyclic graph). This algorithm fails if the graph has a cycle.
2. A DAG may have multiple linear (topological) orderings, but this algorithm returns only one linear order at a time.
3. You need to check for an acyclic graph before you apply a topological sorting algorithm to this graph.
4. The topological sorting algorithm has limited uses. It cannot be used for sorting numbers like other sorting algorithms, i.e., merge sort, quick sort, etc.

Conclusion

Topological sorting arranges vertices in a directed acyclic graph (DAG) so that for every directed edge (u,v), vertex u precedes v in the ordering. This linear ordering is crucial for scheduling, compiling, and resolving dependencies. Implementations in Python can use data structures like adjacency lists, matrices, or dictionaries of sets. Algorithms such as DFS or Kahn’s algorithm efficiently perform topological sorting. And it is the time complexity for this operation. However, topological sorting cannot handle graphs with cycles.

Frequently Asked Questions (FAQs)

Q1: Can topological sorting algorithms handle graphs with disconnected components?

Answer: Yes. You can use topological sorting algorithms on disconnected graphs. The same algorithm can independently sort each connected component. So, there will be a valid topological ordering for the entire graph.

Q2: Can topological sorting be applied to weighted directed graphs?

Answer: Topological sorting is used for unweighted directed graphs. However, it can be extended to weighted graphs by considering edge weights during the sorting process. Weights may affect the order of vertices in the final topological ordering.

Q3: What happens if a graph contains a cycle but topological sorting is still used?

Answer: The algorithm will not generate a valid topological order. Due to cyclic dependencies, it can go into an infinite loop.

Recommended Articles

We hope that this EDUCBA information on “Topological Sorting in Python” was beneficial to you. You can view EDUCBA’s recommended articles for more information,

1. Topological Map
2. Zariski Topology
3. Bus Network Topology
4. Daisy Chain Topology