Depth First Search

Introduction to Depth First Search

Depth First Search for a graph is an important part of the uninformed search strategy. This algorithm is used to perform search activities without any domain knowledge. The algorithm works so that it searches the nodes in a depth-wise fashion, unlike the breadth-first search where a breadth-wise search strategy is applied. It starts operating by searching the root nodes, thereby expanding the successor nodes at that depth. Then it moves to the other node at that depth until the dead-end occurs. The algorithm requires less memory space and time for its execution, even when the required solution lies at the bottom of the tree or graph, unlike the BFS strategy, which employs huge memory and execution time. The DFS algorithm requires the usage of a stack data structure for its implementation. The DFS algorithm works without domain knowledge, which is its hidden strength.

Steps Involved in the DFS Strategy

Now we shall glance at the steps involved in the DFS strategy.

• Step 1: We visit the root node, any starting vertex, and the adjacent unvisited vertex. Then, we mark or label it as visited.
• Step 2: We print it or Display it.
• Step 3: Then, we push it inside a stack.
• Step 4– In case no adjacent vertex is found, we perform the pop operation of the vertex from the stack. This gradually removes all the vertices from the stack that don’t have adjacent nodes.
• Step 5– Then, we reiterate step1 and 2 until all the nodes are visited and the stack is empty.

Example of Depth First Search with Steps

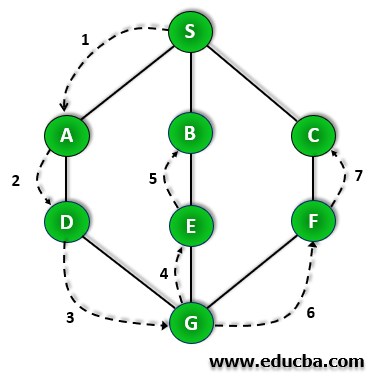
We can now illustrate one example. First, the DFS algorithm is applied to traverse from root node S-A-D-G-E-B, then to F, and at the end to C.

The Graph Traversal Depth Wise Illustration

The steps are as follows.

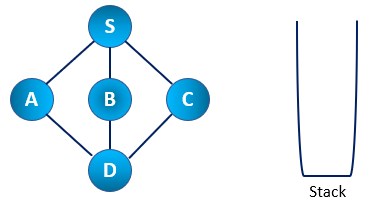
Step 1: First, we initialize the stack to traverse the graph.

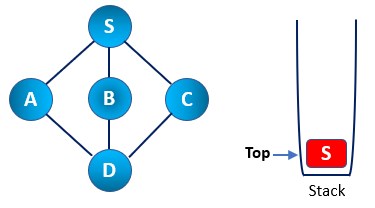
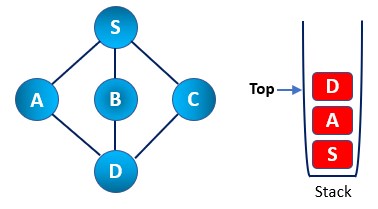
Step 2: Then, we mark the S node as visited and push it into the stack. Then we explore any node that remains unvisited from S. We choose any node out of three available options. Here we have A, B, and C. Let’s say we chose the A node to be visited first and explored further.

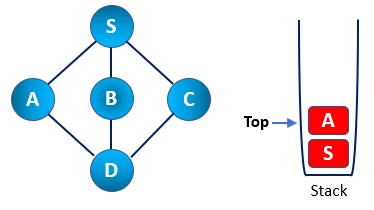
Step 3: We now mark A node as visited and push it back into the stack. Then again, look for new nodes adjacent to node A. Here we have S and D as adjacent nodes. Node S is already explored, so we chose D.

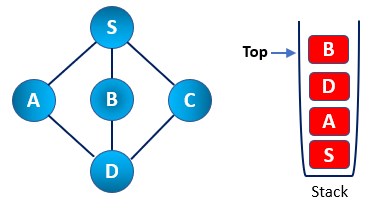
Step 4: Now, we Visit the D node and mark it as a visited node. Then we push it into the stack and move further. Here, we now have B and C nodes, which are unexplored. They are right before node D and unvisited. SO we chose to visit the next B node.

Step 5: We have chosen the B node to visit. Then we mark it as visited and push it into the stack. Now B does not have any adjacent node that remains unvisited. Thus, we start the pop operation. So we pop the B node from the stack.

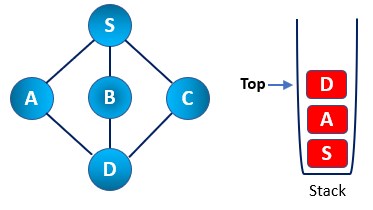
Step 6: Now, we check the stack’s top element, backtrack to the previous node, and check for any adjacent unvisited nodes. So we found a D node on top of the stack.

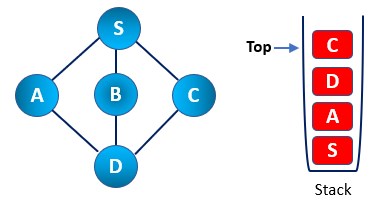
Step 7: Now, we can see only the node that has not yet been visited, i.e., node C from node D. Thus, we visit the C node and mark it as visited, and push it into the stack.

As we can see now C node doesn’t have an unvisited node left, so keep doing the pop operation until we find any node which has not yet been visited. Thus, in the example, we found all the nodes visited already. Thus, we found that the stack was empty at the end of the pop operation.

Now we try to execute the program for DFS implementation using the push and pop operation in the stack data structure.

Program to Implementation DFS in C Language

The Program in C language for DFS implementation is as follows:

#include<stdio.h>
void DFS(int);
int G[10][10],visited[10],m;    //n here is number of vertices and the graph is being sorted in the array G[10][10] void main()
{
int x,y;
printf("Enter the number of vertices in the array:");
scanf("%d",&m);
//read the adjecency matrix
printf("\nEnter the matrix of the graph:");
for(x=0;x<m;x++)
for(y=0;y<m;y++)
scanf("%d",&G[x][y]);
//visited nodes are initialized to zero for our convenience
for(x=0;x<m;x++)
visited[x]=0;
DFS(0);
}
void DFS(int x)
{
int y;
printf("\n%d",x);
visited[x]=1;
for(y=0;y<m;y++)
if(!visited[y]&&G[x][y]==1)
DFS(y);
}

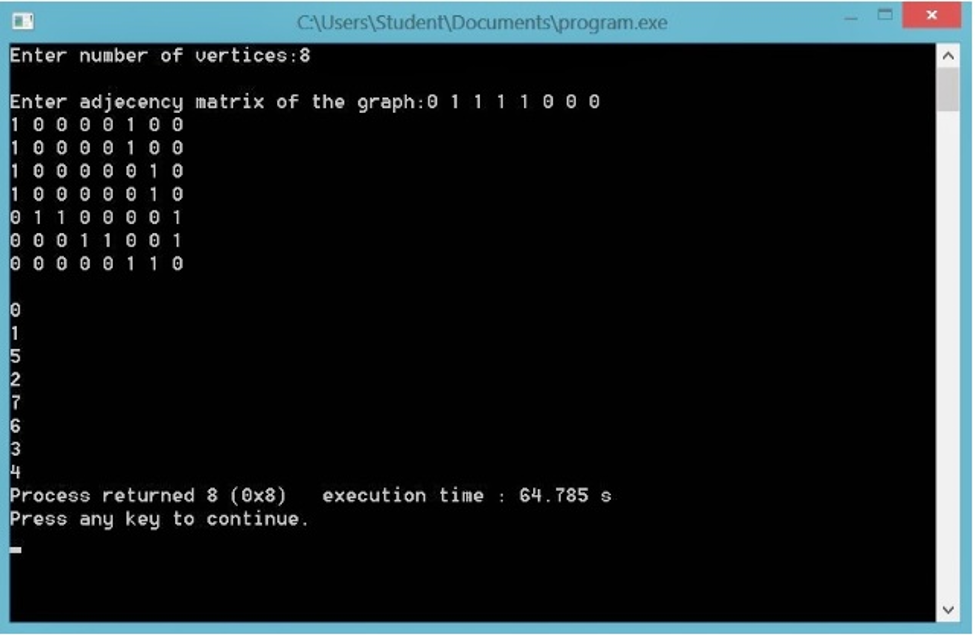
Output:

Applications: There are various applications of the DFS algorithm in computer science. To list a few, DFS is used in detecting a cycle in a graph, in topological sorting, testing a diagram for its bipartite nature, solving puzzles with only one solution, etc.

Complexity:

The run time of the DFS search algorithm is similar to BFS, which is given by:

O (V+E)

• where V = Number of vertices
• E = Number of edges

Advantages of Depth First Search

• The depth-first search algorithm requires less time and memory space.
• DFS assures that the solution will be found if it exists.
• There are huge applications of DFS in graph theory particularly.
• The execution time is expressed as T(V, E) = Θ(1) + Θ(d) + ∑_iT(V_i, E_i), where d can be said to the degree of the root node. V and E are the numbers of vertices and edges.

Disadvantages of Depth First Search

• The run time is believed to be finite, yet it may exceed when the goal node is unknown.
• The algorithm may be reiterating itself without further appreciative progress. There is a fear of an infinite loop in DFS, similar to BFS.

Conclusion

The Depth First search is the algorithm that is naïve to the paths it explores. It follows the Un-informed search strategy, which makes it a powerful strategy on the one hand, and on the other hand, it gives the power for exploring in depth by using less space and time. There are various applications of DFS similar to the BFS strategy.

Recommended Articles

This is a guide to Depth First Search. Here we discuss the introduction and steps involved in the DFS strategy, examples, and code implementation. You may also look at the following articles to learn more –

1. Search Algorithms in AI
2. Azure Functions
3. Amazon Route 53
4. Stack in Data Structure