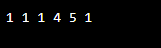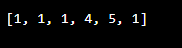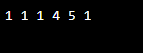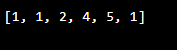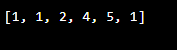Updated February 27, 2023
Definition
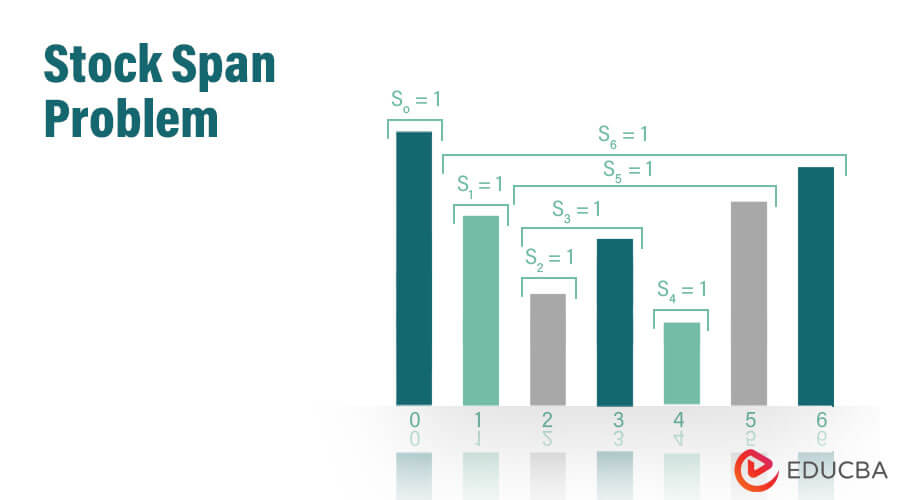
Stock Span Problem comes under economical aspects where we have a series of the stock price quoted for a stock every day and involves calculating the span of the stock price for all number of days, the maximal number of days for which the stock price is equal to or less than the present days. In other words, it involves finding the number of days to the first day, where the stock price of the present day is higher than that of the current day. This problem is used to determine the sentiment of the market.
Introduction to Stock Span Problem
The stock span problem is solved by using the data structures as it provides an effective and efficient way to track the maximum number of days that were successive for which the stock price was equal to or less than to given price. This is a classic problem in finance which involves determining whether the stock price is lower than the current day stock price. The goal of the stock span problem is to find the maximum no. of consecutive days, which is helpful in analyzing the trends of stock price.
This problem is approached by using the data structures as it provides an efficient way to track the stock price. This is an essential financial concept and is widely used in the stock market for decision-making, analysis, and investment. To understand the solution and problem of the stock span, investors make the decisions to take advantage of market trends to maximize the returns of their stock.
Naive Approach – Brute Force
The naïve approach uses brute force to find the span of every stock price. This is done iteratively after counting the number of elements from the left to the right side of the current element that was equal to or greater than the current element. Below is the algorithm of naïve brute force algorithm as follows.
Algorithm:
- Start
- Traverse the price array.
- Run for loop for each i into the 0 to n.
- Iterate the j elements when there is the element to the right-hand side.
- If price j is less than the current price, then increment the count and need to decrement the j.
- Then set the span[i] as count.
- Then return the array of spans.
- Stop
Below are the programs of the naïve approach.
C Language
Code:
#include <stdio.h>
void calspan(int pr[], int n, int S[])
{
S[0] = 1;
for (int a = 1; a < n; a++) {
S[a] = 1;
for (int b = a - 1;
(b >= 0) && (pr[a] >= pr[b]); b--)
S[a]++;
}
}
void printArray (int arr[], int n)
{
for (int a = 0; a < n; a++)
printf ("%d ", arr[a]);
}
int main()
{
int pr[] = { 13, 7, 6, 80, 150, 70 };
int n = sizeof(pr) / sizeof(pr[0]);
int S[n];
calspan(pr, n, S);
printArray(S, n);
return 0;
}Output:
Time complexity – O(N^2)
Auxiliary space – O(N)
C++ Language
Code:
#include <bits/stdc++.h>
using namespace std;
void calsp (int pr[], int n, int S[])
{
S[0] = 1;
for (int a = 1; a < n; a++) {
S[a] = 1;
for (int b = a - 1;
(b >= 0) && (pr[a] >= pr[b]); b--)
S[a]++;
}
}
void par(int arr[], int n)
{
for (int a = 0; a < n; a++)
cout << arr[a] << " ";
}
int main()
{
int pr[] = { 13, 7, 6, 80, 150, 70 };
int n = sizeof(pr) / sizeof(pr[0]);
int S[n];
calsp(pr, n, S);
par(S, n);
return 0;
}Output:
Time complexity – O(N^2)
Auxiliary space – O(N)
Python Language
Code:
def calsp(pr, n, S):
S[0] = 1
for a in range(1, n, 1):
S[a] = 1
b = a - 1
while (b >= 0) and (pr[a] >= pr[b]):
S[a] += 1
b -= 1
def par(arr, n):
for a in range(n):
print(arr[a], end=" ")
pr = [ 13, 7, 6, 80, 150, 70 ]
n = len(pr)
S = [None] * n
calsp(pr, n, S)
par(S, n)Output:
Time complexity – O(N^2)
Auxiliary space – O(N)
Java Language
Code:
import java.util.Arrays;
class naive
{
static void csp(int pr[], int n, int S[])
{
S[0] = 1;
for (int a = 1; a < n; a++) { S[a] = 1; for (int b = a - 1; (b >= 0) && (pr[a] >= pr[b]); b--)
S[a]++;
}
}
static void par(int arr[])
{
System.out.print (Arrays.toString(arr));
}
public static void main(String[] args)
{
int pr[] = { 13, 7, 6, 80, 150, 70 };
int n = pr.length;
int S[] = new int[n];
csp(pr, n, S);
par(S);
}
}Output:
Time complexity – O(N^2)
Auxiliary space – O(N)
Stock Span Problem using Stack
This problem will come with the financial aspect. The consecutive days of the greatest number are given in a stock price that is less than the present price. There are two methods of stock span problem i.e. efficient and inefficient methods. Below is the algorithm of the stock span problem as follows.
Algorithm:
- Start
- Initialize an empty stack.
- After initializing the stack, add the index in the first price of the stack.
- Then iterate the I from 0 to n.
- Then find the greater price of price [i]
- If the stack is not empty and the price is greater than the peak then pop the st.
- If stack is empty, set span[i] = i+1
- Then return span array.
- Stop
C++ Language
Code:
#include <bits/stdc++.h>
using namespace std;
void csp(int pr[], int n, int S[])
{
stack sta;
sta.push(0);
S[0] = 1;
for (int a = 1; a < n; a++) {
while (!sta.empty() && pr[sta.top()] <= pr[a])
sta.pop();
S[a] = (sta.empty()) ? (a + 1) : (a - sta.top());
sta.push(a);
}
}
void par(int arr[], int n)
{
for (int a = 0; a < n; a++)
cout << arr[a] << " ";
}
int main()
{
int pr[] = { 13, 7, 6, 80, 150, 70 };
int n = sizeof(pr) / sizeof(pr[0]);
int S[n];
csp(pr, n, S);
par(S, n);
return 0;
}Output:
Time complexity – O(N)
Auxiliary space – O(N)
Java Language
Code:
import java.util.ArrayDeque;
import java.util.Arrays;
import java.util.Deque;
public class stack {
static void cspan(int pr[], int n, int S[])
{
Deque sta = new ArrayDeque();
sta.push(0);
S[0] = 1;
for (int a = 1; a < n; a++) {
while (!sta.isEmpty()
&& pr[sta.peek()] <= pr[a])
sta.pop();
S[a] = (sta.isEmpty()) ? (a + 1)
: (a - sta.peek());
sta.push(a);
}
}
static void par(int arr[])
{
System.out.print(Arrays.toString(arr));
}
public static void main(String[] args)
{
int pr[] = { 10, 4, 5, 90, 120, 80 };
int n = pr.length;
int S[] = new int[n];
cspan(pr, n, S);
par(S);
}
}Output:
Time complexity – O(N)
Auxiliary space – O(N)
Python Language
Code:
def cspan(price, S):
n = len(pr)
sta = []
sta.append(0)
S[0] = 1
for a in range(1, n):
while(len(sta) > 0 and pr[sta[-1]] <= pr[a]):
sta.pop()
S[a] = a + 1 if len(sta) == 0 else (a - sta[-1])
sta.append(a)
def par(arr, n):
for a in range(0, n):
print(arr[a], end=" ")
pr = [10, 4, 5, 90, 120, 80]
S = [0 for i in range(len(pr)+1)]
cspan(pr, S)
par(S, len(pr))Output:
Time complexity – O(N)
Auxiliary space – O(N)
C Language
Code:
#include
#define MS 100
int stack[MS], top = -1;
void push(int x)
{
if (top == MS -1) {
printf("Stack OF\n");
exit(1);
}
stack[++top] = x;
}
int pop()
{
if (top == -1)
{
printf("stack UF");
exit(1);
}
return stack[top--];
}
int peek()
{
return stack[top];
}
int isEmpty()
{
return top == -1;
}
void stockspan(int pr[], int n, int sp[])
{
sp[0] = 1;
push(0);
for (int a = 1; a < n; a++) { while (!isEmpty() && pr[a] >= pr[peek()]) {
pop();
}
if (isEmpty()) {
sp[a] = a+1;
} else {
sp[a] = a - peek();
}
push(a);
}
}
int main()
{
int pr[] = { 10, 4, 5, 90, 120, 80 };
int n = sizeof(pr) / sizeof(pr[0]);
int sp[n];
stockspan(pr, n, sp);
for (int a = 0; a < n; a++) {
printf("%d", sp[a]);
}
return 0;
}
Output:
Time complexity – O(N)
Auxiliary space – O(N)
Conclusion
The stock span problem is a coding challenge in which we have to find the span of the stock price for the specified day. This is defined as the maximum number of consecutive days before the given day for which the stock price is either lower than or equal to the present day. The stack of the solution decreases the span problem, and it will implement it using the data structure, linked list, and arrays.
Recommended Article
We hope that this EDUCBA information on “Stock Span Problem” was beneficial to you. You can view EDUCBA’s recommended articles for more information,