Updated February 23, 2023
Definition
The right view of a binary tree in Java represents the tree where only the rightmost node of each level is visible. It is a way of looking at the tree that shows only the last element of each tree level. It can be thought of as the set of nodes that would be visible if the tree was viewed from the right side. This can be obtained by traversing the tree using a right-to-left, depth-first search.
Key Takeaways
- These include understanding the basic structure and properties of binary trees, as well as the techniques used for traversing and manipulating them.
- It develops an understanding of the Java programming language and its built-in data structures to implement and test the code effectively.
- In Java, this can be achieved using a queue to keep track of the nodes at each level as they are visited.
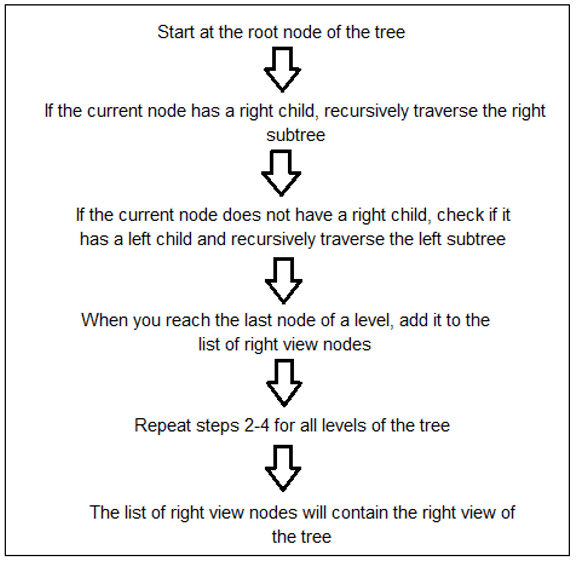
Flow Chart of Java Right View of a Binary Tree
Explanation:
The “right view” of a binary tree refers to the set of nodes that can be seen when the tree is viewed from the right side. In other words, it is the set of nodes that are the rightmost nodes at each tree level. To get the right view of a binary tree in Java, you can use a depth-first traversal (DFS) algorithm, such as pre-order or post-order, or a level-order traversal (BFS) algorithm. In both cases, it is important to keep track of the current depth and compare it to the maximum depth seen so far. If the current depth is greater than the maximum depth, the current node is the rightmost node of that level, so it should be printed.
Example of Right View of a Binary Tree in Java
In a tree where the rightmost element of each level is (1, 3, 7), the right view of the tree would be [1, 3, 7]. To print the right view of a binary tree in Java, you can use a depth-first traversal (DFS) algorithm such as pre-order or post-order.
Code:
// Java program to print right view of binary tree
// A binary tree node
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
// class to access maximum level by reference
class Max_level {
int max_level;
}
class BinaryTree {
Node root;
Max_level max = new Max_level();
// Recursive function to print right view of a binary
// tree.
void rightViewUtil(Node node, int level,
Max_level max_level)
{
// Base Case
if (node == null)
return;
// If this is the last Node of its level
if (max_level.max_level < level) {
System.out.print(node.data + " ");
max_level.max_level = level;
}
// Recur for right subtree first, then left subtree
rightViewUtil(node.right, level + 1, max_level);
rightViewUtil(node.left, level + 1, max_level);
}
void rightView() { rightView(root); }
// A wrapper over rightViewUtil()
void rightView(Node node)
{
rightViewUtil(node, 1, max);
}
// Driver program to test the above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.root.right.left.right = new Node(8);
tree.rightView();
}
}Output:
This code creates a BST with the values 50, 30, 20, 40, 70, 60, and 80 and then performs an in-order traversal of the tree, printing out the values in sorted order. The BST class has methods to insert new nodes and also to traverse the tree in in-order, pre-order, and post-order.
Methods Used for Right View of a Binary Tree in Java
Method #1: Using Recursion
Recursion is a technique where a recursive function is used to traverse the tree and print only the rightmost node of each level.
The function starts by taking the root node of the binary tree as input. It then recursively traverses the right subtree of the current node, and when it reaches the last node of a level, it adds it to a list of right-view nodes.
Code:
import java.util.*;
public class Main {
public static class Node {
int data = 0;
Node left = null;
Node right = null;
Node(int data) {
this.data = data;
}
}
static int idx = 0;
static int max_level = 0;
public static Node create_Tree(int[] arr) {
if (idx == arr.length || arr[idx] == -1) {
idx++;
return null;
}
Node node = new Node(arr[idx++]);
node.left = create_Tree(arr);
node.right = create_Tree(arr);
return node;
}
public static void RightView (Node node, int level) {
if (node == null)
return;
if (max_level < level) {
System.out.print(node.data + " ");
max_level = level;
}
RightView(node.right, level + 1);
RightView(node.left, level + 1);
}
public static void viewSet(Node root) {
RightView(root,1);
}
public static void solve() {
int[] arr = {10,20,30,-1,-1,40,-1,-1,50,60,70,-1,-1,80,90,-1,-1,-1,100,-1,-1 };
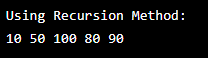
System.out.println("Using Recursion Method: ");
Node root = create_Tree(arr);
viewSet(root);
}
public static void main(String[] args) {
solve();
}
}Output:
Method #2: Using Iterative
Printing the right view of a binary tree in Java using iteration is a technique where a loop, such as a “for” or “while” loop, is used to traverse the tree and print only the rightmost node of each level.
The algorithm uses a queue or a stack to keep track of the nodes at each level. It starts by adding the root node to the queue or stack, then repeatedly dequeues or pops a node from the front of the queue or stack. At each iteration, the algorithm checks the size of the queue or stack, and if it is greater than the current level, it means that the next node is the rightmost node of that level and is printed.
Code:
import java.util.*;
public class Main {
public static class Node {
int data = 0;
Node left = null;
Node right = null;
Node(int data) {
this.data = data;
}
}
static int idx = 0;
public static Node create_Tree(int[] arr) {
if (idx == arr.length || arr[idx] == -1) {
idx++;
return null;
}
Node node = new Node(arr[idx++]);
node.left = create_Tree(arr);
node.right = create_Tree(arr);
return node;
}
public static void RightView(Node node) {
Queue que = new LinkedList<>();
que.add(node);
while (que.size() != 0) {
int size = que.size();
for(int i =0;i<size;i++) {
Node n = que.poll();
if(i== size-1) {
System.out.print(n.data + " ");
}
if(n.left !=null) {
que.add(n.left);
}
if(n.right != null) {
que.add(n.right);
}
}
}
}
public static void solve() {
int [] arr ={10,20,30,-1,-1,40,-1,-1,50,60,70,-1,-1,80,90,-1,-1,-1,100,-1,-1 };
Node root = create_Tree(arr);
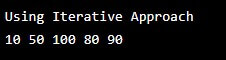
System.out.println("Using Iterative Approach");
RightView(root);
}
public static void main(String[] args) {
solve();
}
}Output:
Please note that this is a basic implementation; it is important to handle the cases where the tree is empty or has only one node. Please also ensure you understand the logic and the data structures used before using it in your code.
FAQ’s
Q1. What is the right view of a binary tree?
Answer: The right view of a binary tree refers to the set of nodes that can be seen when the tree is viewed from the right side. This typically includes the rightmost node at each level of the tree.
Q2. How do I implement a right view of a binary tree in Java?
Answer: The most common way to implement a right view of a binary tree in Java is through a breadth-first traversal of the tree, using a queue to keep track of the nodes at each level as they are visited. During the traversal, the rightmost node at each level is added to a list or array, which represents the right view of the tree.
Q3. What data structure should I use to implement the right view of a binary tree in Java?
Answer: A queue is commonly used to implement a breadth-first traversal of a binary tree, and it can also be used to keep track of the nodes at each level as they are visited. However, an array
Conclusion
The right view of a binary tree in Java is a way of visualizing the tree such that only the rightmost node of each level is visible. The conclusion of this problem would be that by using a DFS algorithm, it is possible to efficiently find by traversing it in post-order and keeping track of the maximum depth seen so far. The node that is first encountered at each depth is added to the right view.
Recommended Article
In this article, you learned about the Right view of a Binary Tree in Java. To know more about the topic, you can refer to these articles.