Updated March 31, 2023
Introduction to Quick sort algorithm
Quick Sort is a sorting technique that sorts the given range of elements and returns that range in sorted order as output. This Algorithm takes an array as input and divides it into many sub-arrays until it matches a suitable condition, merges the elements then returns a sorted array.
Quick Sort follows the divide and conquers approach since the pivot element first divides the range of numbers into sub-arrays and then returns a sorted array as the final step by gathering all the numbers.
How does Quick Sort Algorithm Work?
Before moving on to the algorithm, let’s see how Quick Sort works by taking an example of an array of 7 elements.
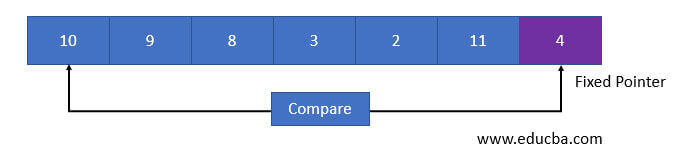
The input array is shown in the below figure.
1. The very first step in Quick Sort includes selecting an element as a pivot element. A pivot element is an element from the array which is selected to act as a division to a range of numbers. If we select ‘n’ as our pivot element, so the numbers from the array which are less than ‘n’ settle at the left side of n, and numbers that are greater than n go to the right of the pivot element. That’s why our first step in Quick Sort is to select an element as a pivot element. The pivot element can be selected in many ways in which some are listed below:
- Pick the first element as the pivot.
- Pick the last element as the pivot.
- Pick a random element as the pivot.
- Pick median as the pivot.
In our example, let’s select the last element as the pivot element and continue the process.
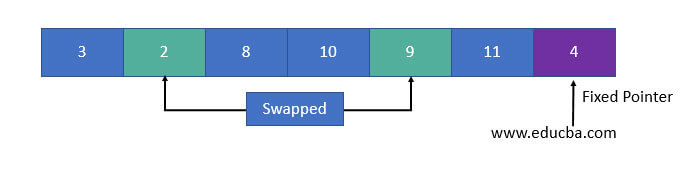
2. The fundamental process in quicksort is a partition(). After selecting the pivot element, we need to rearrange the elements by moving elements that are less than pivot to the left side of the pivot and which are greater than the pivot to the right of the pivot.
The process is shown below:
- A pointer must be fixed at the pivot element.
- Then the pivot element is compared with elements from the beginning.
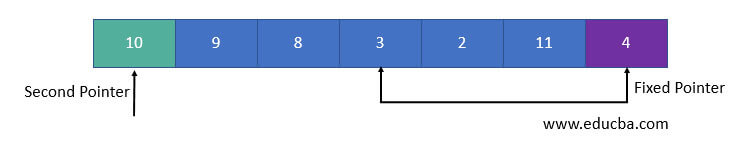
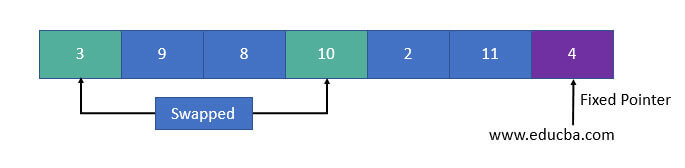
- If the element is greater than the pivot, a second pointer is set for that element. Now, the pivot element is compared with other elements. If an element smaller than the pivot is found, then it is swapped with the greater element, which is in the second pointer.
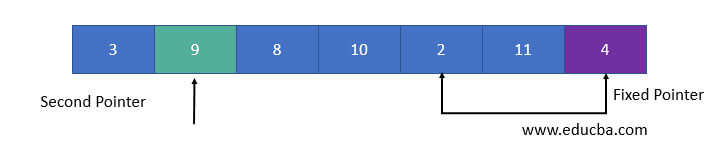
- Again the same process continues to set the next greater element as the second pointer. And it is swapped with the next smaller element.
- The process will continue until the second last element is reached.
- When the second last element is reached, the pivot element will be swapped with the second pointer.
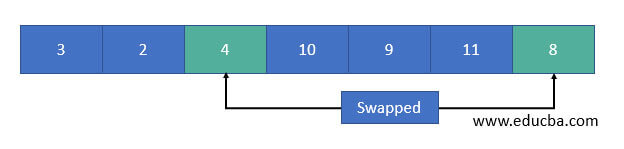
3. Now, the array has been divided into two parts, the first part with elements less than the pivot, second part with elements greater than the pivot.
- Pivot elements are chosen for the left and right sub-arrays separately, and the above process is called recursively for each part until each sub-array is formed into a single element. When this point occurs, the array is already sorted, and the final array is shown below.
Algorithm of Quick Sort
Before moving on to the actual implementation of the QuickSort, let us look at the algorithm.
Step 1: Consider an element as a pivot element.
Step 2: Assign the lowest and highest index in the array to low and high variables and pass it in the QuickSort function.
Step 3: Increment low until array[low] greater than pivot then stop.
Step 4: Decrement high until array[high] less than pivot then stop.
Step 5: Swap low and high and repeat the process until the second last element.
Step 6: Swap pivot and second last element then you will get an array that completed the first partition.
Step 7: Repeat the same process for the two arrays that are obtained until you can no more divide the array.
QuickSort Source Code
# Quick sort in Python
# function to find the partition position
def arraypartition(array, low, high):
# choose the last element as pivot
pivot = array[high]
# second pointer for greater element
i = low - 1
# traverse through all elements by comparing each element with pivot
for j in range(low, high):
if array[j] <= pivot:
# if element smaller than pivot is found then swap it with the greater element pointed by i
i = i + 1
# swapping element at i with element at j
(array[i], array[j]) = (array[j], array[i])
# swap the pivot element with the greater element specified by i
(array[i + 1], array[high]) = (array[high], array[i + 1])
# return the position of partition
return i + 1
# function to perform quicksort
def quickSort(array, low, high):
if low < high:
# find pivot element such that
# element smaller than pivot are on the left
# element greater than pivot are on the right
pi = arraypartition(array, low, high)
# recursive call on the left of pivot
quickSort(array, low, pi - 1)
# recursive call on the right of pivot
quickSort(array, pi + 1, high)
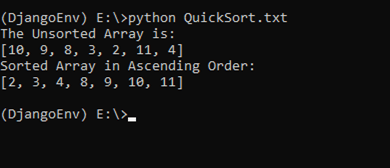
array = [10, 9, 8, 3, 2, 11, 4]
print("The Unsorted Array is: ")
print(array)
quickSort(array, 0, len(array) - 1)
print('Sorted Array in Ascending Order:')
print(array)
Output:
Time Complexities
Worst-case complexity
Worst Case Complexity O(n2) occurs when the pivot element is either the greatest or the smallest among all the elements in the array. This leads to the case in which the pivot element lies at the end of the array.
Best Case Complexity
Best Case Complexity O(n*log n) occurs when the pivot element lies in the middle or near the middle element in the array.
Average Case Complexity
Average Case Complexity O(n*log n) occurs when we don’t exactly get evenly balanced partitions of the array.
Conclusion
- Quick Sort follows the divide and conquers approach and sorts the given range of elements and returns that range in sorted order as output.
- A pivot element is an element from the array which is selected to act as a division to a range of numbers.
- You can select any element as a pivot element.
Recommended Articles
This is a guide to Quick sort algorithm. Here we discuss How does Quick Sort Algorithm Work along with the codes and outputs. You may also have a look at the following articles to learn more –