Pearson Correlation Coefficient Formula (Table of Contents)
What is the Pearson Correlation Coefficient Formula?
The Pearson Correlation Coefficient is used to identify the strength of a linear interrelation between two variables; we don’t need to measure if there is no linear relation between two variables. It’s also called a product-moment correlation coefficient (PMCC) and denoted by “r” and is frequently used as a statistical measure. The correlation coefficient for continuous data scales lies between -1 to +1.
If the value is near to positive 1, this means there is a perfect positive interrelation between the two variables; it indicates that if one variable increases positively, the other variable also increases in the same direction. On the other side, if the value is near to negative 1, this means that there is a perfect negative correlation. This indicates that if one variable increases positively, the other one will decrease perfectly in the opposite direction and vice versa. If the value is 0, then there is no interrelation between the two variables.
Formula,
Where,
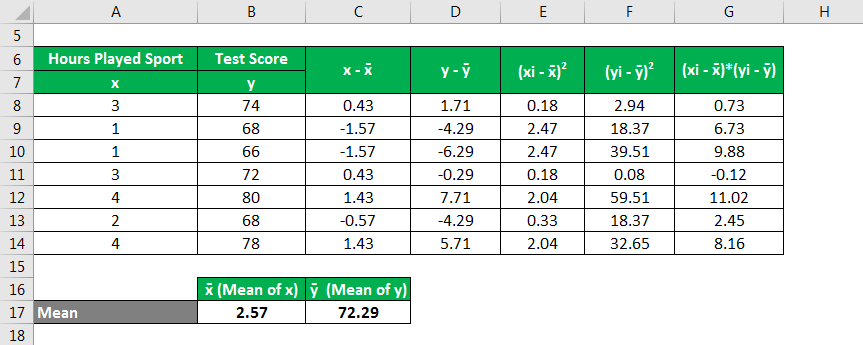
x̄ = Mean of x variable
ȳ = Mean of y variable
Example of Pearson Correlation Coefficient Formula (With Excel Template)
Let’s take an example to understand the calculation of the Pearson Correlation Coefficient in a better manner.
Pearson Correlation Coefficient Formula – Example #1
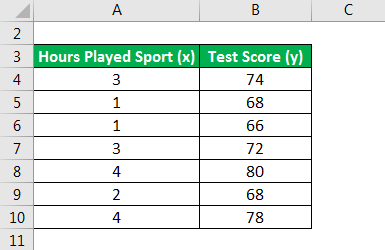
Let’s take a simple example to understand the Pearson correlation coefficient. Mark is a scholar student, and he is good at sports as well. But after some time, he reduced his sports activity and then observed that he is scoring lesser marks in tests. To test his hypothesis, he tracked how he scored in his tests; based on how many hours he plays any sport before he appears in the school tests. He gathered the following data to cheque the correlation between hours of sports he is playing and his tests score.
Solution:
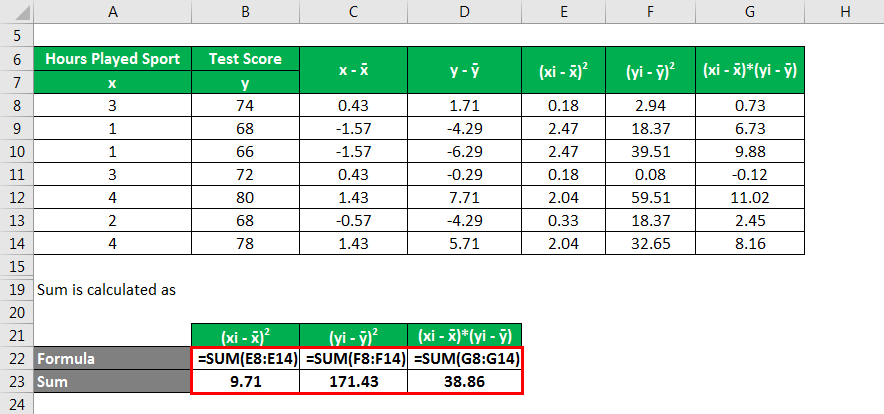
Sum(x,y) Variable is calculated as
S(x,y) Variable =38.86
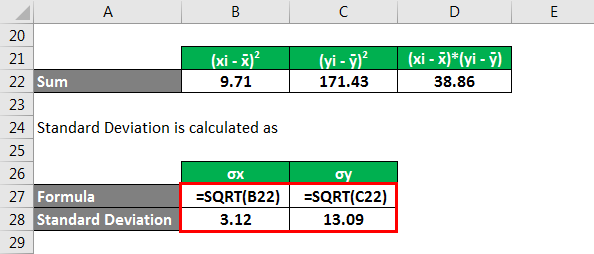
Standard Deviation of x is calculated as
- Standard Deviation x = (xi – x̄)2
- Standard Deviation y = (yi – ȳ)2
- Standard Deviation x = 3.12
- Standard Deviation y= 13.09
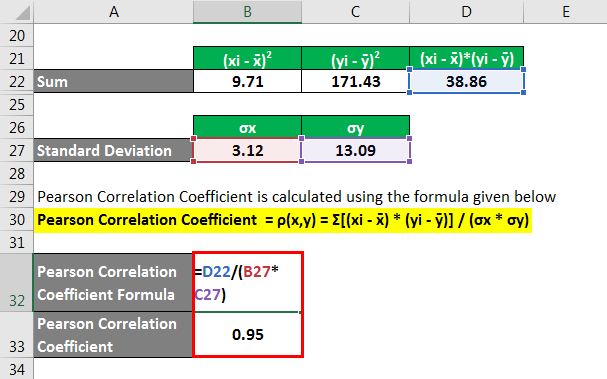
Pearson Correlation Coefficient is calculated using the formula given below.
Pearson Correlation Coefficient = ρ(x,y) = Σ(xi – x̄)(yi – ȳ) / σx*σy
4.5 (7,384 ratings)
View Course
- Pearson Correlation Coefficient = 38.86/(3.12*13.09)
- Pearson Correlation Coefficient = 0.95
We have an output of 0.95; this indicates that when the number of hours played to increase, the test scores also increase. These two variables are positively correlated.
Pearson Correlation Coefficient Formula – Example #2
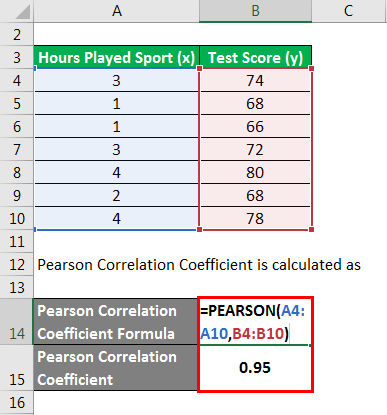
Let’s take the same example and calculate the Pearsons Correlation Coefficient by using an excel formula.
Solution:
To calculate the Pearson correlation coefficient in excel, we need to apply a simple formula.
Pearson Correlation Coefficient is calculated as
Pearson Correlation Coefficient = 0.95.
Where array 1 is a set of independent variables and array 2 is a set of independent variables. In this example, we have calculated the same 1st example with the excel method, and we have got the same result, i.e. 0.95.
Pearson Correlation Coefficient Formula – Example #3
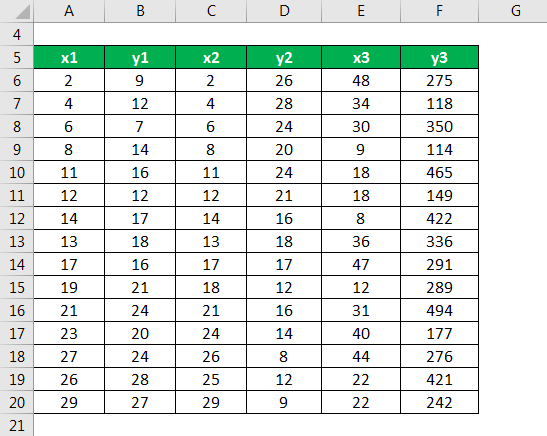
In our last example, we will not perform and calculations and understand as well as analyze the various interrelation between variables and their correlation coefficients with the help of the scatter diagram. We are looking at three different sets of data and plotting them on a scatter graph.
Solution:
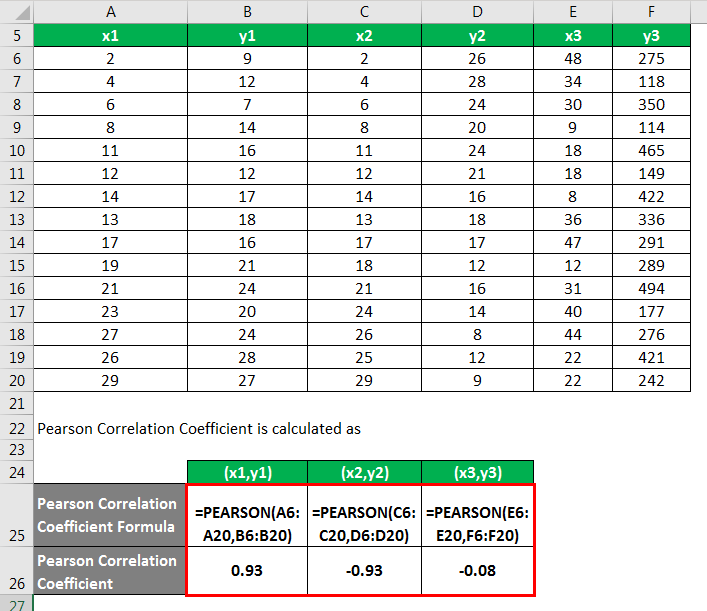
Calculating the Pearson Correlation Coefficient using excel formula.
Pearson Correlation Coefficient = PEARSON(array1,array2)
Following are observations of the above case :
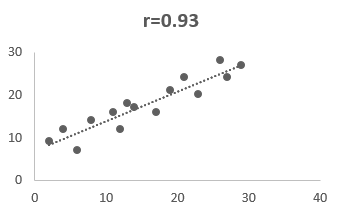
The diagram, which has a value, r = 0.93, This represents that both the variables are highly positively correlated, which means if there is a positive increase in one variable, the other one will also increase.
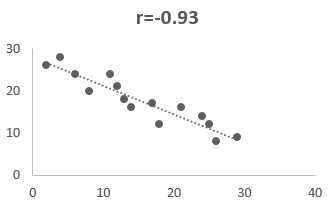
The diagram, which has a value, r = -0.93, This represents that both the variables are highly negatively correlated, which shows us if there is a positive increase in one variable, the other one will decrease significantly.
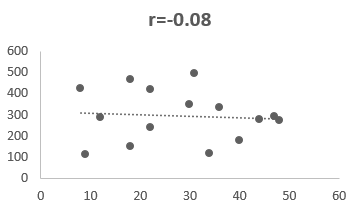
The diagram, which has r = -0.08, represents us that there is no relationship between the variables. In short, they both are independent variables.
The conclusion is that the stronger the interrelation between variable when the value of r is near to +1 or -1. In other words, the closer the value of r to 0, the higher the difference between the two variables.
Explanation
The formula for the Pearson Correlation Coefficient can be calculated by using the following steps:
Step 1: Gather the data of the variable and label the variables x and y.
Step 2: Firstly, we need to calculate the mean of both the variables and then solve the below equation using the variables data.
Σ(xi – x̄)(yi – ȳ)
Step 3: Next, we need to calculate the Standard Deviation of both the variables, formulae to calculate standard deviation is:
√(Σ(xi – x̄)²) * √(Σ(yi – ȳ)²)
Step 4: Finally, to calculate the Pearson Correlation Coefficient, divide the covariance of the variables (derived in step1) by the standard deviation of both the variables (derived in step 2).
ρ(x,y) = Σ(xi – x̄)(yi – ȳ) / σx*σy
Relevance and Use of Pearson Correlation Coefficient Formula
Pearson correlation coefficient is used to measures the direction between two linear associated variables. In other words, it determines whether there is a linear association between two continuous variables. Pearson correlation used widely in multiple sectors like Agriculture, Manufacturing, Health, Medical, etc. it helps the analyst to understand the strength and the relationships between the variables like demand and supply of product, income, and expenditures. It helps us to understand economic behavior. However, you would not unremarkably need to pursue a Pearson’s correlation to see the strength and direction of a linear relationship once you already understand the connection between you two variables is not linear. It reduces the effect scope of unpredictability; the prediction based on PCC is near to reality.
Pearson Correlation Coefficient Calculator
You can use the following Pearson Correlation Coefficient Formula Calculator
| (xi - x̄)(yi - ȳ) | |
| σx | |
| σy | |
| Pearson Correlation Coefficient | |
| Pearson Correlation Coefficient = |
| |||||||||
|
Recommended Articles
This is a guide to the Pearson Correlation Coefficient Formula. Here we discuss how to calculate the Pearson Correlation Coefficient Formula along with practical examples. We also provide a Pearson Correlation Coefficient calculator with a downloadable excel template. You may also look at the following articles to learn more –
