Introduction to Multicollinearity
When several independent variables are highly but not perfectly correlated among themselves, the regression result is unreliable, this phenomenon is known as Multicollinearity, and as a consequence, we are not able to disprove the null hypothesis, wherein we should actually reject the same. In the process of multiple regression, where the impact of changes in many independent variables is being analyzed on one dependent variable, we make a few assumptions that all aim at the validity of the result of regression. If any of these assumptions are violated, our regression result becomes invalid. One such violation is known as ‘Multicollinearity’.
Multiple Regression Equation
A generic form of the multiple regression equation is given below:
- Here Y is the dependent variable
- b0 is the intercept variable, which shows the value of Y when all independent variables are 0, and there is no error term
- X1 to Xi are all independent variables the change of which impacts the change in Y
- b1 to bi are the coefficients of the independent variables, sometimes known as the slope coefficients, which determine the magnitude of the change in Y to a change in X
- Finally is the error term, which incorporates the impact on Y, which can’t be attributed to a change in any of the independent variables. For a good regression equation, the error term should be as small as possible because that implies that the impact on Y can be reasonably explained by the chosen independent variables.
Assumptions and Violations of Multiple Regression
For a reliable process of Multiple Regression, we make a few assumptions (listed below), and the violations of these lead to a misleading regression output. Sometimes this phenomenon is referred to as GIGO in the domain of computer science, which stands for Garbage-in-garbage- out, i.e. if the input is unreliable or contaminated, the output will also be unreliable or contaminated:
- Dependent variable Y and independent variables X1…Xi are linearly related.
- The independent variables X1…Xi is not random, and no linear relationship exists between any of these (the violation of this assumption is known as Multicollinearity)
- The expected value of the error terms associated with each independent variable is 0. This is assumed so that we can be reasonably sure that the independent variable are good indicators of the dependent variable
- The variance of Error term is the same for all observations (Homoskedasticity and the violation is called Heteroskedasticity)
- Error terms are not correlated (Violation is called Serial correlation)
- The error term is normally distributed.
We need to know that these are the assumptions of multiple regression; however, from the point of view of this article, our focus is on the violation of one single assumption. Violations of other assumptions are also a part of statistical theory and are studied in great detail.
Impact of Multicollinearity
In the process of coming to a regression output, we undergo the process of Hypothesis testing. Herein, we specify two hypotheses, the first one being a Null Hypothesis symbolized by H0, which is generally the opposite of the desired result, and therefore we have to disprove it through the process of regression. The second hypothesis is called the Alternate Hypothesis, which generally encompasses the desired result and is symbolized by Ha, which gets proven automatically when the Null Hypothesis gets rejected.
Due to the existence of Multicollinearity, we are not able to reject the Null Hypothesis, where had there been no Multicollinearity, it would have been rejected. Therefore, we are not able to reasonably say that our regression is meaningful.
4.6 (11,985 ratings)
View Course
Detection of Multicollinearity
We need to find the anomaly in our regression output to come to the conclusion that Multicollinearity exists. Steps reading to this conclusion are as follows:
1. R2 is High
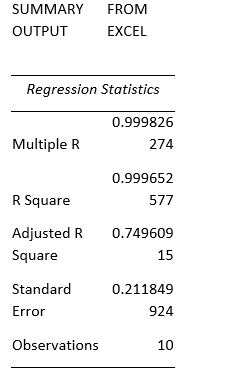
R2, also known as the coefficient of determination, is the degree of variation in Y that can be explained by the X variables. Therefore, a higher R2 number implies that a lot of variation is explained through the regression model. In multiple regression, we use something known as an Adjusted R2, which is derived from the R2, but it is a better indicator of the predictive power of regression as it determines the appropriate number of independent variables for the model. In spite of a high adjusted R2, if we say that the regression is not meaningful, then we can suspect Multicollinearity.
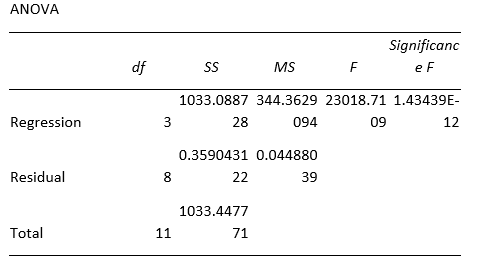
2. F–stat is Significant
This is the test conducted to reject the null hypothesis, which states that all the slope coefficients in the regression equations are equal to 0. If this statistic is significant, then we can reject the null hypothesis and safely say that at least one slope coefficient is not equal to 0, and therefore some part of the change in Y can be explained through a change in one or more X variables. So one of the indicators of the presence of Multicollinearity is that F-stat is highly significant, and still we can’t say that our regression model has good predicting power.
3. T–stat is Insignificant
This is the last straw. If the first two points are true, we look at the T-stat of each of the X variables, and if it is insignificant, and thus we are unable to reject the null hypothesis, then we should check for Multicollinearity. We set up a Null Hypothesis for the slope coefficient of each of the X variables. If our view is that the coefficient should be negative, we have the following one-tailed T-test Hypotheses:
- H0: bi ≥ 0
- Ha: bi < 0
4. T–stat = bi – 0 / Standard Error
bi is the predicted value of the slope coefficient, and 0 is the hypothesized value.
We assume a certain significance level and compare the T-stat to the critical value at that level and then come to the conclusion, whether the slope coefficient is significant or not, and if it is insignificant, then we can conclude the presence of Multicollinearity
In the case of Multicollinearity, the standard errors are unnaturally inflated, leading to the inability to reject the null hypothesis for the T stat. In certain software packages, they provide a measure for the same, known as the VIF, and a VIF >5 suggests high Multicollinearity.
Example of Multicollinearity (With Excel Template)
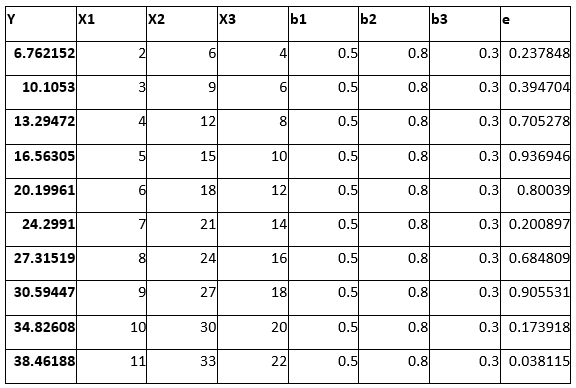
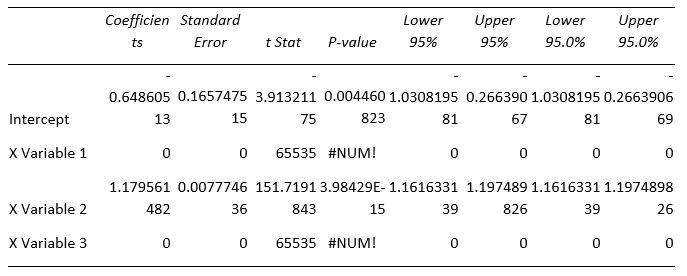
Below are the examples to implement Multicollinearity:
- Here, as we can see X2 = 3 x X1 and X3 = 2 x X1, therefore, all the independent variables correlated as per the definition of multicollinearity,
- However, producing a regression output using Excel gives num error because this dataset contains a violation of regression assumptions i.e. multicollinearity. That is excel cannot calculate the regression for such an input that contains the violation. Other software packages contain different calculation methods such as VIF and therefore they are able to run a regression with data containing multicollinearity.
- I don’t have any other software to generate the output. Therefore I used the example from a book with all the sources mentioned because generating results is not possible without specific software. Kindly let me know what should I do?
Please see the link explaining why a num error occurs: https://exceljet.net/formula/how-to-fix-the-num-error
Conclusion
One of the ways to remove the effect of Multicollinearity is to omit one or more independent variables and see the impact on the regression output. One of the practical problems of Multicollinearity is that it can’t be completely eliminated. In the real world, the factors affecting a dependent variable are somewhat correlated. At the maximum, we can only consider the degree of this correlation and then act accordingly. A low degree of correlation is preferred.
Recommended Articles
This is a guide to Multicollinearity. Here we discuss multiple regression equations, assumptions, and violations with impact, detection, and example to implement in multicollinearity. You can also go through our other related articles to learn more –
