Introduction to Merge Sorting Algorithms in Java
Merge Sorting Algorithms are very important in Computer Science. The output of sorting is to arrange the elements of a list to a certain order (either ascending or descending). Merge sort is one of the most efficient sorting algorithms available, based on the concept of divide and conquer. As the name suggests, first divide the bigger problem into small problems, then solve the smaller problems to solve the bigger problem. In this article, we will discuss Merge Sorting Algorithms in Java.
Table of Contents
- Introduction
- Working on Merge Sort in Java
- Implementation of Merge Sorting Algorithms in Java
- Algorithm & Pseudocode
- Merge Sorting Algorithms in Java
- When should we use the Merge Sort?
- Complexity Analysis of Merge Sort
- Comparing Merge Sort with Other Algorithms
Programmers and coders extensively use various sorting techniques in Java to ensure they address all possible ways of arranging data.
Some of the popular techniques used in Java for sorting algorithms are described below.
- Bubble sort
- Selection sort
- Insertion sort
- Heap sort
- Merge sort
Apart from the above-mentioned techniques, other techniques such as Quicksort, can be used for sorting data sequentially.
Conceptually, Merge sort is a combination of two basic algorithms called MERGE and MERGE_SORT, which works as follows:
- Divide the unsorted list into n number of single-item sub-lists (n is the total number of elements in the unsorted list).
- Merge sublists repeatedly into sorted sublists until forming a single sorted list.
Working on Merge Sort in Java
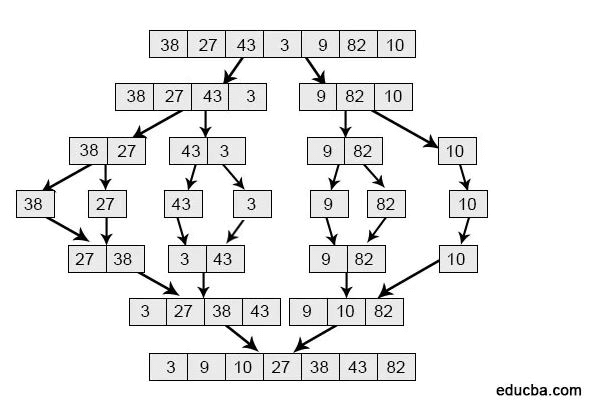
Now, we will see the working of the Merge Sort mechanism invented by John Von Neumann in 1945, which Java uses to arrange data sequentially. Merge Sort In Java is quite similar to the Quick Sort mechanism. It is also referred to as a divide-and-conquer algorithm. In simple words, it divides the array into two halves. After that, it sorts the two arrays in a respective order as the user desires. Then, it merges the two halves and easily becomes a complete single sorted array. Now, suppose there is an array called arr[]. The merge sort mechanism divides the array first into two halves. Then, it sorts the respective halves, getting a sorted array at each end. Finally, the two halves are also equated to whether the left index is greater than the right or vice versa, and then the number is put into the array. In this way, the array is sorted.
The below diagram shows how an array is sorted using merge sort.
Implementation of Merge Sorting Algorithms in Java
The MERGE algorithm is the procedure of combining two sorted lists into one sorted list.
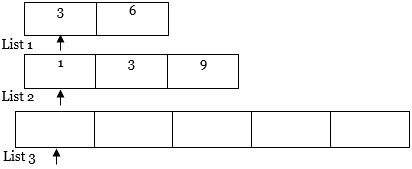
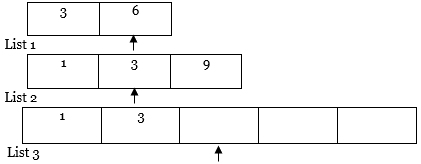
Example: Suppose there are two lists, i.e., List 1 {6,3} and List 2 {3,1,9}.
1. First, sort both the lists.
List 1
List 2
Now, we will apply a merging technique to it.
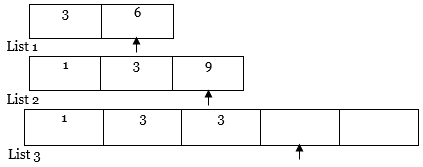
2. Then, we will create a new list of size m+n where m is the number of elements in List 1, and n is the number of elements in List 2.
List 3
In our case, m=2 and n=3, so m+n= 5.
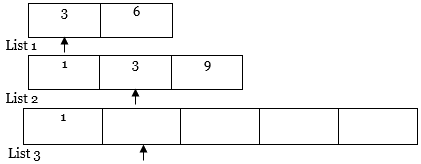
3. Now, we have a two-pointer. A first pointer points at the first position of List 1, and a Second pointer points at the first position of List 2.
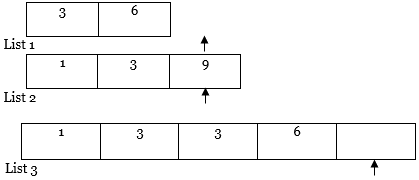
4. Then, we will compare the value of both pointers. For the pointer with a lesser value, copy that element into List 3 and move the pointer to the right of the list with a smaller value and the resultant list (i.e., List 1 and List 3).
5. Similarly, perform step 4 again and again.
Further traversing…..
Algorithm & Pseudocode
The two Algorithms used in the Merge sort in Java are:
- The MERGE(ARR, F, M, L) is a process that assumes the following:
- ARR[F ….M] and ARR[M+ 1….L] are sorted lists.
- Merges the two sorted sub-lists into one ARR[F….L].
- SORT(ARR[], F, L) //here, F is the first and L is the last index of the array.
If ( L > 1 )
1. Find the middle point to divide the list into two halves:
middle M = (F +L)/2
2. Call Merge Sort for the first half:
Call SORT(ARR, 1, M)
3. Call Merge Sort for the second half:
Call SORT(ARR, M+ 1, L)
4. Merge the halves sorted in steps 2 and 3:
Call MERGE(ARR, L, M, R)
Examples of Merge Sorting Algorithms in Java
Here are examples of using the merge sort algorithm in Java programming.
Example #1
In the first example, we will observe the sorting of a series of numbers in an array. Sorting numbers is straightforward because they do not have associated ASCII values like alphabets or names. The following program shows the sorting in merge sort fashion, sorting numbers in ascending order. There are two arrays, the Left Array and the Right Array. The array has 10 numbers that have been arranged in ascending order, that is, from smallest to largest.
Code
import java.util.*;
public class Main {
void merge(int arr[], int beg, int mid, int end) {
int l = mid - beg + 1;
int r = end - mid;
int LeftArray[] = new int[l];
int RightArray[] = new int[r];
for (int i = 0; i < l; ++i)
LeftArray[i] = arr[beg + i];
for (int j = 0; j < r; ++j)
RightArray[j] = arr[mid + 1 + j];
int i = 0, j = 0;
int k = beg;
while (i < l && j < r) {
if (LeftArray[i] <= RightArray[j]) {
arr[k] = LeftArray[i];
i++;
} else {
arr[k] = RightArray[j];
j++;
}
k++;
}
while (i < l) {
arr[k] = LeftArray[i];
i++;
k++;
}
while (j < r) {
arr[k] = RightArray[j];
j++;
k++;
}
}
void sort(int arr[], int beg, int end) {
if (beg < end) {
int mid = (beg + end) / 2;
sort(arr, beg, mid);
sort(arr, mid + 1, end);
merge(arr, beg, mid, end);
}
}
public static void main(String args[]) {
int arr[] = {90, 23, 101, 45, 65, 23, 67, 89, 34, 23};
Main ob = new Main(); // Corrected class name
ob.sort(arr, 0, arr.length - 1); // Corrected method call
System.out.println("\nSorted array");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " "); // Corrected println to print
}
}
}Output:
Example #2
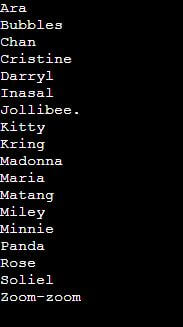
In the second example, we observe them actively applying the Merge sort technique to sort alphabets or names in Java. In this program, names of persons are taken in any random order. The mergeSort() function initially arranges the names in alphabetical order. Subsequently, we compare the LeftMergeSort() and RightMergeSort() functions to determine the alphabetical precedence of names.
Code
import java.util.*;
public class NewClass {
public static void main(String[] args) {
String[] OneGo = { "Kring", "Panda", "Soliel", "Darryl", "Chan", "Matang", "Jollibee.", "Inasal" };
String[] TwoGo = { "Minnie", "Kitty", "Madonna", "Miley", "Zoom-zoom", "Cristine", "Bubbles", "Ara", "Rose", "Maria" };
String[] nameGo = new String[OneGo.length + TwoGo.length];
mergeSort(OneGo);
mergeSort(TwoGo);
merge(nameGo, OneGo, TwoGo);
mergeSort(nameGo);
//Arrays.sort(names);
for (String ClassThree: nameGo) {
System.out.println(ClassThree);
}
}
public static void mergeSort(String[] nameGo) {
if (nameGo.length > 1) {
String[] leftGo = new String[nameGo.length / 2];
String[] rightGo = new String[nameGo.length - nameGo.length / 2];
for (int so = 0; so < leftGo.length; so++) {
leftGo[so] = nameGo[so];
}
for (int ki = 0; ki < rightGo.length; ki++) {
rightGo[ki] = nameGo[ki + nameGo.length / 2];
}
mergeSort(leftGo);
mergeSort(rightGo);
merge(nameGo, leftGo, rightGo);
}
}
public static void merge(String[] nameH, String[] leftH, String[] rightH) {
int as = 0;
int bs = 0;
for (int i = 0; i < nameH.length; i++) {
if (bs >= rightH.length || (as < leftH.length && leftH[as].compareToIgnoreCase(rightH[bs]) < 0)) {
nameH[i] = leftH[as];
as++;
} else {
nameH[i] = rightH[bs];
bs++;
}
}
}
}The sample output in this program is also shown below, which sorts the names in alphabetical order.
Output
Example #3
Let us take an example of an array ARR {10,6,8,5,7,3,4}. We will use the Merge Algorithm to sort the Array using its Divide and divide-and-conquer technique.
Code:
import java.util.Scanner;
public class Main {
// merges two sublists of arr[].
// first list is arr[l..m]
// second list is arr[m+1..r]
void mergeAlgo(int arr[], int l, int m, int r)
{
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L[] = new int [n1];
int R[] = new int [n2];
// copy data to temp arrays
for (int i=0; i<n1; ++i)
L[i] = arr[l + i];
for (int j=0; j<n2; ++j)
R[j] = arr[m + 1+ j];
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// copy remaining elements of L[] if any
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
// copy remaining elements of R[] if any
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
// main function that sorts arr[l..r] using mergeAlgo()
void sort(int arr[], int l, int r)
{
if (l < r)
{
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr , m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
}
}
/* A function to print list of size n */
static void printArray(int arr[])
{
int n = arr.length;
for (int i=0; i<n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
public static void main(String args[]) {
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr[] = new int[N];
for (int i = 0; i < arr.length; i++) {
arr[i] = myObj.nextInt();
}
Main mg = new Main(); // Corrected class name
mg.sort(arr, 0, arr.length - 1);
System.out.println("\nSorted list:");
printArray(arr);
}
}Output:
Example #4
Here is a code example showing the implementation of merge sort in Java:
Code:
public class MergeSort {
private int[] array;
private int[] tempMergedArr;
private int length;
public static void main(String a[]){
int[] inputArr = {18, 8, 4, 13, 10, 12, 7, 11};
MergeSort mergeSort = new MergeSort();
mergeSort.sort(inputArr);
for(int i:inputArr){
System.out.print(i + " ");
}
}
public void sort(int inputArr[]) {
this.array = inputArr;
this.length = inputArr.length;
this.tempMergedArr = new int[length];
performMergeSort(0, length - 1);
}
private void performMergeSort(int lowerIndex, int higherIndex) {
if (lowerIndex < higherIndex) {
int middle = lowerIndex + (higherIndex - lowerIndex) / 2;
// Sort the left side of the array call performMergeSort recursively
performMergeSort(lowerIndex, middle);
// Sort the right side of the array call performMergeSort recursively
performMergeSort(middle + 1, higherIndex);
// Merge subparts using a temporary array
mergeData(lowerIndex, middle, higherIndex);
}
}
private void mergeData (int lowerIndex, int middle, int higherIndex) {
for (int i = lowerIndex; i <= higherIndex; i++) {
tempMergedArr[i] = array[i];
}
int i = lowerIndex;
int j = middle + 1;
int k = lowerIndex;
while (i <= middle && j <= higherIndex) {
if (tempMergedArr[i] <= tempMergedArr[j]) {
array[k] = tempMergedArr[i];
i++;
} else {
array[k] = tempMergedArr[j];
j++;
}
k++;
}
while (i <= middle) {
array[k] = tempMergedArr[i];
k++;
i++;
}
}
}The above code will produce a sorted array as output.
Output:
When should we use the Merge Sort?
Merge sort can be used in the following scenarios:
- When sorting a data structure that does not support random access, merge sort can be helpful and efficient.
- Merge sort becomes a suitable choice for situations demanding a high level of parallelism since multiple processes can independently solve distinct subproblems by running in parallel.
- Merge sort is quicker when working with linked lists because pointers can easily be changed while merging the lists.
- Merge Sort exhibits stability, signifying that identical elements in an array retain their original positions relative to each other. When a high degree of stability is essential, one may opt for Merge Sort.
Complexity Analysis of Merge Sort
Below points analysis complexity of merge sort:
- Merge sort is a recursive algorithm, and its time complexity is O(n*log n) in all three cases (worst, best, and average) as merge sort divides the array into two halves and takes linear time to merge them.
- Space Complexity of merge sort is O (n) as it operates on the recursive approach. Hence, merge sort can be considered as a fast, space, and time-efficient algorithm.
Comparing Merge Sort with Other Algorithms
Below points compare merge sort with other algorithms:
- Heap Sort has the same time complexity as merge sort but requires only O (1) auxiliary space instead of merge sort’s O (n). Hence, heap sort is more space-efficient than merge sort.
- Quick Sort implementations generally outperform merge sort for sorting RAM-based arrays.
- Merge sort outperforms quick sort and heap sort algorithms when working with the linked list, as pointers can easily be changed.
Conclusion
Merge sort shares the same time complexities for best, worst, and average cases, enhancing its efficiency compared to other sorting techniques. It outpaces alternative algorithms, demonstrating its speed. The applicability of merge sort extends to files of any size, adding to its versatility. The algorithm’s high parallelizability results from employing the divide-and-conquer method. To foster a robust foundation in computer science, it is advisable to gain a comprehensive understanding of various sorting algorithms.
Recommended Articles
We hope that this EDUCBA information on “Merge Sorting Algorithms in Java” was beneficial to you. You can view EDUCBA’s recommended articles for more information.