Updated February 28, 2023
Introduction to Matlab mesh()
The Matlab built-in function mesh() is a 3D plotting function to create 3- dimensional surface plot with respect to the values from the input matrix. The plot generated from mesh() is a surface graphic object which is wireframe parametric by nature. This function maps the input matrix values to color values, generating color maps. The height of the plot depends on the input matrix value, above to x-y plane that can be defined by X, Y coordinate inputs. The color for the plot is determined depending on the surface height.
Syntax:
This 3D surface plotting function can be implement with different syntaxes depending on input arguments, provided to the function call.
Different syntax and their respective input arguments are described in the below table:
| Syntax | Description |
| mesh(Z) | It is used to generate 3D surface plot of which x, y co-ordinates are decided by column and row indices of the input matrix ‘Z’. |
| mesh(Z,C) | It is used to generate 3D surface plot for input matrix ‘Z’ with the color for the edges set to ‘C’. |
| mesh(X,Y,Z) | It is used to generate 3D surface plot of which height is determined by the values in the input matrix ‘Z’ and the x-y plane is set by X and Y. |
| mesh(X,Y,X,C) | It is used to generate 3D surface plot of which on the x-y plane, set by X and Y, with edge color ‘C’. |
| mesh(ax,____) | It is used to generate the 3D surface plot with the new axis ‘ax’. |
| mesh(__,name, value) | It is used to set surface properties for the plot using name-value pair argument format. |
| Cs=mesh(___) | It is used to store the 3D plot generated from the function mesh() in chart surface object. The object can be used to modify the surface object properties after the plot is generated. |
Examples of Matlab mesh()
Given below are the examples mentioned:
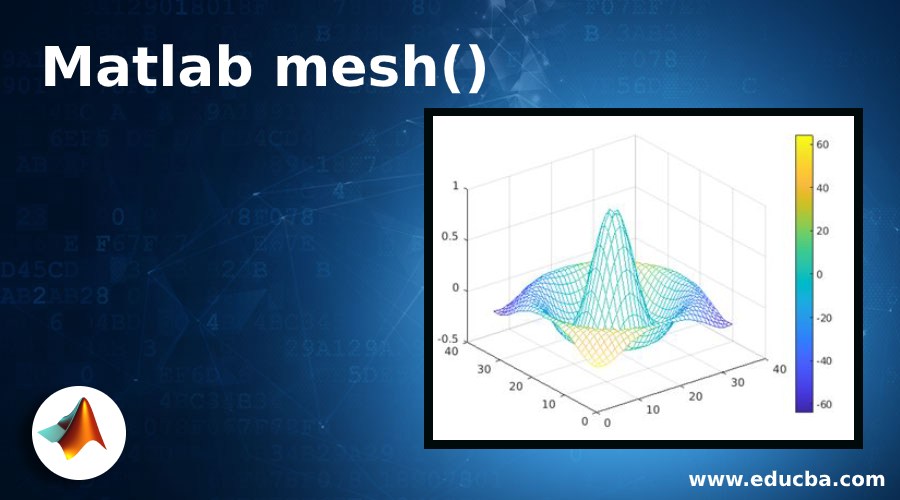
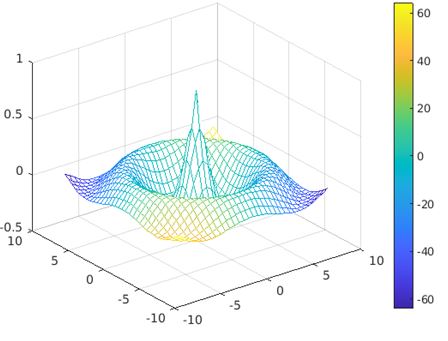
Example #1 – Using mesh(Z)
The below code snippet is used to generate 3D plot for the input matrix ‘I’ which is function of x-coordinate ‘P’ and y-co-ordinates ‘R’ providing ‘I’ as single input argument to the mesh() function call.
Code:
[P,Q] = meshgrid(-8:.5:8);
R = sqrt(P.^2 + Q.^2);
I = sin(R)./R;
mesh(I)
Output:
The plot is generated with the default color value depending on the data values in the input matrix.
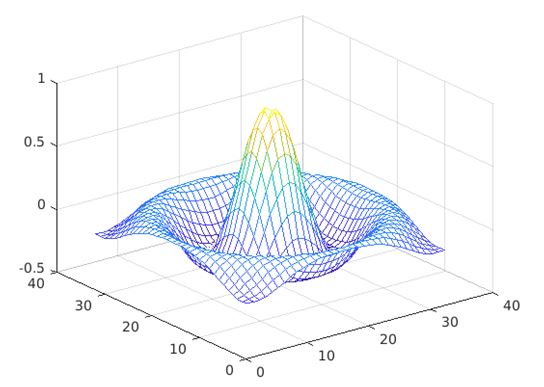
Example #2 – Using mesh(Z, C)
The below set of command is defined to change the color of the same plot generated in the previous function defining the input argument ‘C’.
Code:
[P,Q] = meshgrid(-8:.5:8);
R = sqrt(P.^2 + Q.^2);
I = sin(R)./R;
C = P.*Q;
mesh(I,C)
colorbar
Output:
The color value is set by the input argument ‘C’ which is being designed as function of the x,y coordinates ‘P’ and ‘Q’.
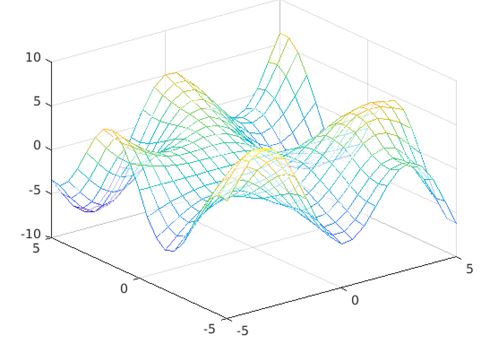
Example #3 – Using mesh(X, Y, Z)
The code written below generates 3D surface plot from mesh() function which accepts 3 input arguments i.e. input matrix ‘Z’ , x,y coordinate inputs ‘P’ and ‘Q’.
Code:
[P,Q] = meshgrid(-8:.5:8);
R = sqrt(P.^2 + Q.^2) + eps;
Z = cos(R)./(R+1.2);
mesh(P,Q,Z)
Output:
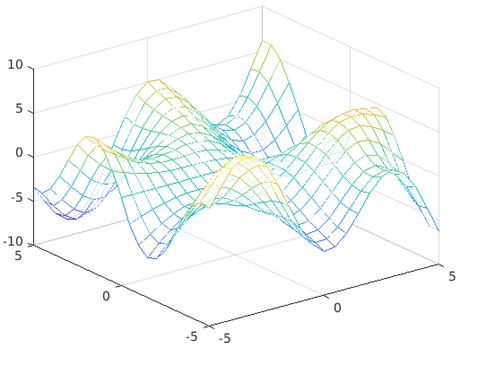
Example #4 – Using mesh(X, Y, Z, C)
The below set of command is defined to change the color of the same plot generated in the previous function defining the input argument ‘C’.
Code:
[P,Q] = meshgrid(-8:.5:8);
R = sqrt(P.^2 + Q.^2) + eps;
Z = cos(R)./(R+1.2);
C = P.*Q;
mesh(P,Q,Z,C)
colorbar
Output:
The color value is set by the input argument ‘C’ which is being designed as function of the x,y coordinates ‘P’ and ‘Q’.
Example #5 – Using mesh(__,name, value)
Matlab supports the feature to alter the display of the generated plot using name-value pairing format in mesh() function. The attribute given as name in the pair gets set with the data given as value in the function call.
Some of the attributes which can be altered to customize the plot, are given in the table below:
| Attribute | Description |
| EdgeColor | The attribute is used to decide the color for the edge lines of the plot. Possible values are none, flat, interp, RGB triplets, color name etc. |
| LineStyle | It is used to set the line style for the representation of the 3D surface plot. Possible values are‘-‘ (solid line), ‘- -‘ (dashed line) , ‘:’ (dotted line) etc. |
| FaceColor | This attribute customize the face of the color in the plot. Possible values are flat, interp, RGB triplets, texture map, hexadecimal color code etc. |
| FaceAlpha | It decides the degree of transparency for the faces of the plot. Possible values are any value between 0 to 1. |
| FaceLighting | This attribute is used to decide the effect of the light objects on the plot faces. Possible values are flat, gouraud, none etc. |
a. With FaceAlpha=0.6
The transparency of the faces of the plot is resulted with FaceAlpha being set to 0.6.
Code:
[P,Q] = meshgrid(-5:.5:5);
R = Q.*cos(P) - P.*sin(Q);
mesh(P,Q,R,'FaceAlpha','0.6')
Output:
b. With facealpha=0.8
Code:
[P,Q] = meshgrid(-5:.5:5);
R = Q.*cos(P) - P.*sin(Q);
mesh(P,Q,R,'FaceAlpha','0.8')
The transparency of the faces of the plot is changed as value for FaceAlpha is updated from 0.6 to 0.8.
Output:
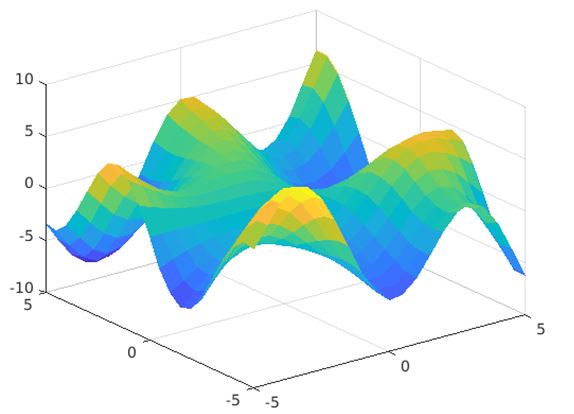
c. With Facecolor=flat
Code:
[P,Q] = meshgrid(-5:.5:5);
R = Q.*cos(P) - P.*sin(Q);
mesh(P,Q,R,'FaceColor','flat')
Output:
The resultant plot is presented with faces having different color for each face depending on the value present in CData property.
Example #6 – Using Cs=mesh(___)
The below code returns surface object from the function which is stored in the chart surface object ‘cs’. The display of the plot is altered by modifying the value for EdgeColor and LineStyle by calling the attributes through ‘cs’ object.
Code:
[P,Q] = meshgrid(-5:.5:5);
R = Q.*cos(P) - P.*sin(Q);
cs=mesh(P,Q,R);
cs.EdgeColor='interp';
cs.LineStyle='-.'
Output:
The resultant plot is represented having edges with interpolated coloring depending on the values in the CData property and the lines are displayed following the style format ‘-.’.
Additional Note:
- The default behavior of Matlab regarding the plot generation using mesh() function is it computes the color limits depending on the minimum and maximum value of from the input matrix. The intermediate values get mapped to the current color map by means of the process of linear transformation, performed by Matlab.
- In the process of generating the surface plot, the simulation of hidden surface elimination is carried out by ‘hidden’ command and that of shading model is controlled by ‘shading command’.
Recommended Articles
This is a guide to Matlab mesh(). Here we discuss the introduction to Matlab mesh() with examples with better understanding. You may also have a look at the following articles to learn more –