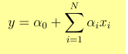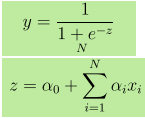Updated March 23, 2023
Difference Between Linear Regression and Logistic Regression
Linear regression is an algorithm that is based on the supervised learning domain of machine learning. It inherits a linear relationship between its input variables and the single output variable where the output variable is continuous in nature. It is used to predict the value of output let’s say Y from the inputs let’s say X. When only single input is considered it is called simple linear regression. Logistic Regression is a form of regression which allows the prediction of discrete variables by a mixture of continuous and discrete predictors. It results in a unique transformation of dependent variables which impacts not only the estimation process but also the coefficients of independent variables. It addresses the same question which multiple regression does but with no distributional assumptions on the predictors. In logistic regression the outcome variable is binary. The purpose of the analysis is to assess the effects of multiple explanatory variables, which can be numeric or categorical or both.
Categories of Linear Regression
It can be classified into two main categories:
1. Simple Regression
Principal of operation: The main goal is to find out the equation of a straight line that best fits the sampled data. This equation algebraically describes the relationship between the two variables. The best-fitting straight line is called as regression line.
Y = β0 + β1 X
Where,
β represents the features
β0 represents the intercept
β1 represents the coefficient of feature X
2. Multivariable Regression
It is used to predict a correlation between more than one independent variable and one dependent variable. Regression with more than two independent variable is based on fitting shape to the constellation of data on a multi-dimensional graph. The shape of regression should be such that it minimizes the distance of the shape from every data point.
A linear relationship model can be represented mathematically as below:
Y = β0 + β1 X1 + β2X2 + β3X3 + ....... + βnXn
Where,
β represents the features
β0 represents the intercept
β1 represents the coefficient of feature X1
βn represents the coefficient of feature Xn
Advantages and Disadvantages of Linear Regression
Below given are advantages and disadvantages:
Advantages
- Due to its simplicity, it is widely used modeling for predictions and inferences.
- It focuses on data analysis and data preprocessing. So, it deals with different data without bothering about the details of the model.
Disadvantages
- It works efficiently when the data are normally distributed. Thus for efficient modeling, the collinearity must be avoided.
Types of Logistic Regression
Below are the 2 types of Logistic Regression:
1. Binary Logistic Regression
It is used when the dependent variable is dichotomous i.e. like a tree with two branches. It is used when the dependent variable is non-parametric.
Used when
- If there is no linearity
- There are only two levels of the dependent variable.
- If multivariate normality is doubtful.
2. Multinomial Logistic Regression
Multinomial logistic regression analysis requires that the independent variables be metric or dichotomous. It does not make any assumptions of linearity, normality, and homogeneity of variance for the independent variables.
It is used when the dependent variable has more than two categories. It is used to analyze relationships between a non-metric dependent variable and metric or dichotomous independent variables, then compares multiple groups through a combination of binary logistic regressions. In the end, it provides a set of coefficients for each of the two comparisons. The coefficients for the reference group are taken to be all zeros. Finally, prediction is done based on the highest resultant probability.
Advantage of logistic regression: It is a very efficient and widely used technique as it doesn’t require many computational resources and doesn’t require any tuning.
Disadvantage of logistic regression: It cannot be used for solving non-linear problems.
Head to Head comparison between Linear Regression and Logistic Regression (Infographics)
Below are the top 6 differences between Linear Regression vs Logistic Regression
Key Difference Between The Linear Regression and Logistic Regression
Let us discuss some of the major key differences between Linear Regression vs Logistic Regression
Linear Regression
- It is a linear approach
- It uses a straight line
- It can’t take categorical variables
- It has to ignore observations with missing values of the numeric independent variable
- Output Y is given as
- 1 unit increase in x increases Y by α
Applications
- Predicting the price of a product
- Predicting score in a match
Logistic Regression
- It is a statistical approach
- It uses a sigmoid function
- It can take categorical variables
- It can take decisions even if observations with missing values are present
- Output Y is given as, where z is given as
- 1 unit increase in x increases Y by log odds of α
- If P is the probability of an event, then (1-P) is the probability of it not occurring. Odds of success = P / 1-P
Applications
- Predicting whether today it will rain or not.
- Predicting whether an email is a spam or not.
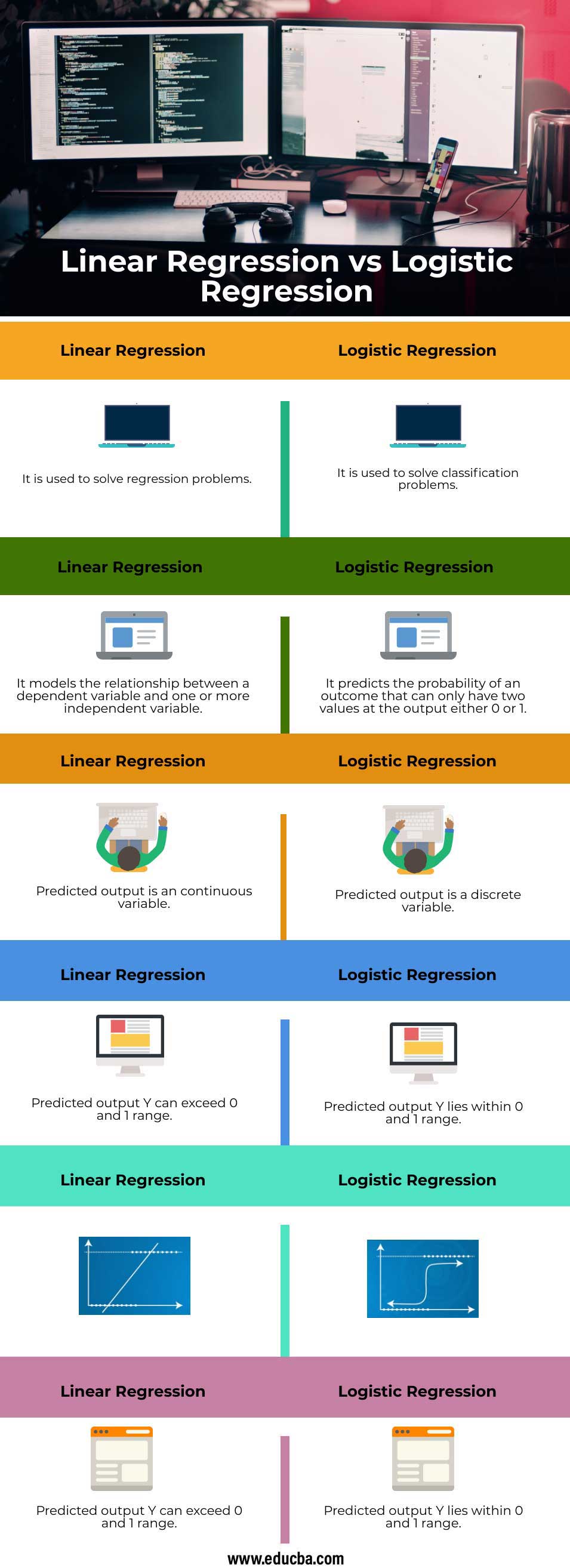
Linear Regression vs Logistic Regression Comparison Table
Let’s discuss the top comparison between Linear Regression vs Logistic Regression
|
Linear Regression |
Logistic Regression |
| It is used to solve regression problems | It is used to solve classification problems |
| It models the relationship between a dependent variable and one or more independent variable | It predicts the probability of an outcome that can only have two values at the output either 0 or 1 |
| The predicted output is a continuous variable | The predicted output is a discrete variable |
| Predicted output Y can exceed 0 and 1 range | Predicted output Y lies within 0 and 1 range |
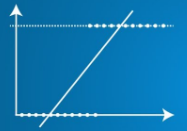 |
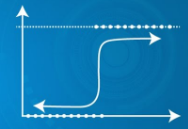 |
| Predicted output Y can exceed 0 and 1 range | Predicted output |
Conclusion
If features doesn’t contribute to prediction or if they are very much correlated with each other then it adds noise to the model. So, features which doesn’t contribute enough to the model must be removed. If independent variables are highly correlated it may cause a problem of multi-collinearity, which can be solved by running separate models with each independent variable.
Recommended Articles
This has been a guide to Linear Regression vs Logistic Regression . Here we discuss the Linear Regression vs Logistic Regression key differences with infographics, and comparison table. You may also have a look at the following articles to learn more–